2016年山东省淄博市中考数学试卷
试卷更新日期:2016-06-21 类型:中考真卷
一、选择题
-
1. 人类的遗传物质是DNA,DNA是一个很长的链,最短的22号染色体与长达30000000个核苷酸,30000000用科学记数法表示为( )
A、3×107 B、30×104 C、0.3×107 D、0.3×1082. 计算|﹣8|﹣(﹣ )0的值是( )A、﹣7 B、7 C、7 D、93.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )
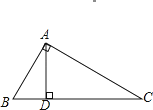 A、2条 B、3条 C、4条 D、5条4. 关于x的不等式组 ,其解集在数轴上表示正确的是( )A、
A、2条 B、3条 C、4条 D、5条4. 关于x的不等式组 ,其解集在数轴上表示正确的是( )A、 B、
B、 C、
C、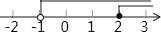 D、
D、 5. 下列特征量不能反映一组数据集中趋势的是( )A、众数 B、中位数 C、方差 D、平均数6. 张老师买了一辆启辰R50X汽车,为了掌握车的油耗情况,在连续两次加油时做了如下工作:
5. 下列特征量不能反映一组数据集中趋势的是( )A、众数 B、中位数 C、方差 D、平均数6. 张老师买了一辆启辰R50X汽车,为了掌握车的油耗情况,在连续两次加油时做了如下工作:①把油箱加满油;
②记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:
加油时间
加油量(升)
加油时的累计里程(千米)
2016年4月28日
18
6200
2016年5月16日
30
6600
则在这段时间内,该车每100千米平均耗油量为( )
A、3升 B、5升 C、7.5升 D、9升7.如图,△ABC的面积为16,点D是BC边上一点,且BD= BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )
 A、3 B、4 C、5 D、68.
A、3 B、4 C、5 D、68.如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
 A、 B、 C、 D、10﹣59.
A、 B、 C、 D、10﹣59.如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是( )
 A、 B、1 C、 D、210.
A、 B、1 C、 D、210.小明用计算器计算(a+b)c的值,其按键顺序和计算器显示结果如表:

这时他才明白计算器是先做乘法再做加法的,于是他依次按键:

从而得到了正确结果,已知a是b的3倍,则正确的结果是( )
A、24 B、39 C、48 D、9611.如图,直线l1∥l2∥l3 , 一等腰直角三角形ABC的三个顶点A,B,C分别在l1 , l2 , l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则 的值为( )
 A、 B、 C、 D、12.
A、 B、 C、 D、12.反比例函数y= (a>0,a为常数)和y= 在第一象限内的图象如图所示,点M在y= 的图象上,MC⊥x轴于点C,交y= 的图象于点A;MD⊥y轴于点D,交y= 的图象于点B,当点M在y= 的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )
 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
13. 计算 的结果是 .14.
由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
 15. 若x=3﹣ ,则代数式x2﹣6x+9的值为 .16. 某快递公司的分拣工小王和小李,在分拣同一类物件时,小王分拣60个物件所用的时间与小李分拣45个物件所用的时间相同.已知小王每小时比小李多分拣8个物件,设小李每小时分拣x个物件,根据题意列出的方程是 .17.
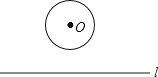
15. 若x=3﹣ ,则代数式x2﹣6x+9的值为 .16. 某快递公司的分拣工小王和小李,在分拣同一类物件时,小王分拣60个物件所用的时间与小李分拣45个物件所用的时间相同.已知小王每小时比小李多分拣8个物件,设小李每小时分拣x个物件,根据题意列出的方程是 .17.如图,⊙O的半径为2,圆心O到直线l的距离为4,有一内角为60°的菱形,当菱形的一边在直线l上,另有两边所在的直线恰好与⊙O相切,此时菱形的边长为 .
三、解答题
-
18.
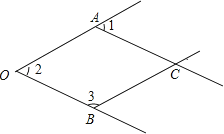
如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
 19. 解方程:x2+4x﹣1=0.20. 下面是淄博市2016年4月份的天气情况统计表:
19. 解方程:x2+4x﹣1=0.20. 下面是淄博市2016年4月份的天气情况统计表:日期
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
天气
多云
阴
多云
晴
多云
阴
晴
晴
晴
多云
多云
多云
晴
晴
雨
日期
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
天气
雨
多云
多云
多云
多云
晴
多云
多云
晴
多云
多云
多云
晴
晴
晴
(1)、请完成下面的汇总表:天气
晴
多云
阴
雨
天数
(2)、根据汇总表绘制条形图;(3)、在该月中任取一天,计算该天多云的概率.21.如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
 (1)、求这条抛物线对应的函数解析式;(2)、求直线AB对应的函数解析式.22.
(1)、求这条抛物线对应的函数解析式;(2)、求直线AB对应的函数解析式.22.如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
 (1)、求证:AE=AF;(2)、求证:BE= (AB+AC).23.
(1)、求证:AE=AF;(2)、求证:BE= (AB+AC).23.已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0, ),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为 .
 (1)、求a的值;(2)、当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;(3)、当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF.24.
(1)、求a的值;(2)、当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;(3)、当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF.24.如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
 (1)、求证: = ;(2)、求证:AF⊥FM;(3)、请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.
(1)、求证: = ;(2)、求证:AF⊥FM;(3)、请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.