2016年山东省滨州市中考数学试卷

试卷更新日期：2016-06-21 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣1²等于（　　）

A、1 B、﹣1 C、2 D、﹣2

查看试题解析
2.
如图，AB∥CD，直线EF与AB，CD分别交于点M，N，过点N的直线GH与AB交于点P，则下列结论错误的是（　　）

A、∠EMB=∠END B、∠BMN=∠MNC C、∠CNH=∠BPG D、∠DNG=∠AME

查看试题解析
3. 把多项式x²+ax+b分解因式，得（x+1）（x﹣3）则a，b的值分别是（　　）

A、a=2，b=3 B、a=﹣2，b=﹣3 C、a=﹣2，b=3 D、a=2，b=﹣3

查看试题解析
4. 下列分式中，最简分式是（　　）

A、 $\frac{x^{2} - 1}{x^{2} + 1}$ B、 $\frac{x + 1}{x^{2} - 1}$ C、 $\frac{x^{2} - 2 x y + y^{2}}{x^{2} - x y}$ D、 $\frac{x^{2} - 36}{2 x + 12}$

查看试题解析
5.
某校男子足球队的年龄分布如图所示，则根据图中信息可知这些队员年龄的平均数，中位数分别是（　　）

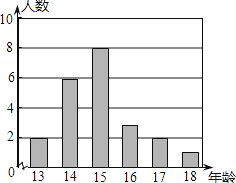A、15.5，15.5 B、15.5，15 C、15，15.5 D、15，15

查看试题解析
6.
如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（　　）

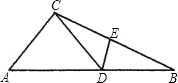A、50° B、51° C、51.5° D、52.5°

查看试题解析
7.
如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（﹣3，2），（b，m），（c，m），则点E的坐标是（　　）

A、（2，﹣3） B、（2，3） C、（3，2） D、（3，﹣2）

查看试题解析
8. 对于不等式组 ${\begin{cases} \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \\ 5 x + 2 > 3 (x - 1) \end{cases}$ 下列说法正确的是（　　）

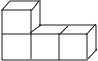
A、此不等式组无解 B、此不等式组有7个整数解 C、此不等式组的负整数解是﹣3，﹣2，﹣1 D、此不等式组的解集是﹣ $\frac{5}{2}$ ＜x≤2

查看试题解析
9.
如图是由4个大小相同的正方体组合而成的几何体，其主视图是（　　）

A、 B、 C、 D、

查看试题解析
10. 抛物线y=2x²﹣2 $\sqrt{2}$ x+1与坐标轴的交点个数是（　　）

A、0 B、1 C、2 D、3

查看试题解析
11. 在平面直角坐标系中，把一条抛物线先向上平移3个单位长度，然后绕原点旋转180°得到抛物线y=x²+5x+6，则原抛物线的解析式是（　　）

A、y=﹣（x﹣ $\frac{5}{2}$ ）²﹣ $\frac{11}{4}$ B、y=﹣（x+ $\frac{5}{2}$ ）²﹣ $\frac{11}{4}$ C、y=﹣（x﹣ $\frac{5}{2}$ ）²﹣ $\frac{1}{4}$ D、y=﹣（x+ $\frac{5}{2}$ ）²+ $\frac{1}{4}$

查看试题解析
12.
如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：
①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的是（　　）

A、②④⑤⑥ B、①③⑤⑥ C、②③④⑥ D、①③④⑤

查看试题解析

二、填空题

13. 有5张看上去无差别的卡片，上面分别写着0，π， $\sqrt{2}$ ， $\frac{1}{9}$ ，1.333．随机抽取1张，则取出的数是无理数的概率是．

查看试题解析
14. 甲、乙二人做某种机械零件，已知甲是技术能手每小时比乙多做3个，甲做30个所用的时间与乙做20个所用的时间相等，那么甲每小时做个零件．

查看试题解析
15.
如图，矩形ABCD中，AB= $\sqrt{3}$ ，BC= $\sqrt{6}$ ，点E在对角线BD上，且BE=1.8，连接AE并延长交DC于点F，则 $\frac{C F}{C D}$ = ．

查看试题解析
16.
如图，△ABC是等边三角形，AB=2，分别以A，B，C为圆心，以2为半径作弧，则图中阴影部分的面积是

查看试题解析
17.
如图，已知点A、C在反比例函数y= $\frac{a}{x}$ 的图象上，点B，D在反比例函数y= $\frac{b}{x}$ 的图象上，a＞b＞0，AB∥CD∥x轴，AB，CD在x轴的两侧，AB= $\frac{3}{4}$ ，CD= $\frac{3}{2}$ ，AB与CD间的距离为6，则a﹣b的值是．

查看试题解析
18. 观察下列式子：
1×3+1=2²；
7×9+1=8²；
25×27+1=26²；
79×81+1=80²；
…
可猜想第2016个式子为．

查看试题解析

三、解答题：

19. 先化简，再求值： $\frac{a - 4}{a}$ ÷（ $\frac{a + 2}{a^{2} - 2 a}$ ﹣ $\frac{a - 1}{a^{2} - 4 a + 4}$ ），其中a= $\sqrt{2}$ ．

查看试题解析
20. 某运动员在一场篮球比赛中的技术统计如表所示：
技术
上场时间（分钟）
出手投篮（次）
投中
（次）
罚球得分
篮板
（个）
助攻（次）
个人总得分
数据
46
66
22
10
11
8
60
注：表中出手投篮次数和投中次数均不包括罚球．
根据以上信息，求本场比赛中该运动员投中2分球和3分球各几个．

查看试题解析
21.
如图，过正方形ABCD顶点B，C的⊙O与AD相切于点P，与AB，CD分别相交于点E、F，连接EF．

(1)、求证：PF平分∠BFD．

(2)、若tan∠FBC= $\frac{3}{4}$ ，DF= $\sqrt{5}$ ，求EF的长．

查看试题解析
22. 星期天，李玉刚同学随爸爸妈妈回老家探望爷爷奶奶，爸爸8：30骑自行车先走，平均每小时骑行20km；李玉刚同学和妈妈9：30乘公交车后行，公交车平均速度是40km/h．爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同，路程均为40km/h．设爸爸骑行时间为x（h）．

(1)、请分别写出爸爸的骑行路程y₁（km）、李玉刚同学和妈妈的乘车路程y₂（km）与x（h）之间的函数解析式，并注明自变量的取值范围；

(2)、请在同一个平面直角坐标系中画出（1）中两个函数的图象；

(3)、请回答谁先到达老家。

查看试题解析
23.
如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．

(1)、请判断四边形EBGD的形状，并说明理由；

(2)、若∠ABC=30°，∠C=45°，ED=2 $\sqrt{10}$ ，点H是BD上的一个动点，求HG+HC的最小值．

查看试题解析
24.
如图，已知抛物线y=﹣ $\frac{1}{4}$ x²﹣ $\frac{1}{2}$ x+2与x轴交于A、B两点，与y轴交于点C

(1)、求点A，B，C的坐标；

(2)、点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；

(3)、此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析