2016年福建省福州市中考数学试卷
试卷更新日期:2016-06-21 类型:中考真卷
一、选择题
-
1. 下列实数中的无理数是( )A、0.7 B、 C、π D、﹣82.
如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3.
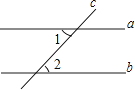
3.如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
 A、同位角 B、内错角 C、同旁内角 D、对顶角4. 下列算式中,结果等于a6的是( )A、a4+a2 B、a2+a2+a2 C、a2•a3 D、a2•a2•a25. 不等式组 的解集是( )A、x>﹣1 B、x>3 C、﹣1<x<3 D、x<36. 下列说法中,正确的是( )A、不可能事件发生的概率为0 B、随机事件发生的概率为 C、概率很小的事件不可能发生 D、投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次7. A,B是数轴上两点,线段AB上的点表示的数中,有互为相反数的是( )A、
A、同位角 B、内错角 C、同旁内角 D、对顶角4. 下列算式中,结果等于a6的是( )A、a4+a2 B、a2+a2+a2 C、a2•a3 D、a2•a2•a25. 不等式组 的解集是( )A、x>﹣1 B、x>3 C、﹣1<x<3 D、x<36. 下列说法中,正确的是( )A、不可能事件发生的概率为0 B、随机事件发生的概率为 C、概率很小的事件不可能发生 D、投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次7. A,B是数轴上两点,线段AB上的点表示的数中,有互为相反数的是( )A、 B、
B、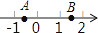 C、
C、 D、
D、 8. 平面直角坐标系中,已知▱ABCD的三个顶点坐标分别是A(m,n),B(2,﹣1),C(﹣m,﹣n),则点D的坐标是( )A、(﹣2,1) B、(﹣2,﹣1) C、(﹣1,﹣2) D、(﹣1,2)9.
8. 平面直角坐标系中,已知▱ABCD的三个顶点坐标分别是A(m,n),B(2,﹣1),C(﹣m,﹣n),则点D的坐标是( )A、(﹣2,1) B、(﹣2,﹣1) C、(﹣1,﹣2) D、(﹣1,2)9.如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
 A、(sinα,sinα) B、(cosα,cosα) C、(cosα,sinα) D、(sinα,cosα)10. 下表是某校合唱团成员的年龄分布
A、(sinα,sinα) B、(cosα,cosα) C、(cosα,sinα) D、(sinα,cosα)10. 下表是某校合唱团成员的年龄分布年龄/岁
13
14
15
16
频数
5
15
x
10﹣x
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A、平均数、中位数 B、众数、中位数 C、平均数、方差 D、中位数、方差11. 已知点A(﹣1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可以是( )A、 B、
B、 C、
C、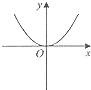 D、
D、 12. 下列选项中,能使关于x的一元二次方程ax2﹣4x+c=0一定有实数根的是( )A、a>0 B、a=0 C、c>0 D、c=0
12. 下列选项中,能使关于x的一元二次方程ax2﹣4x+c=0一定有实数根的是( )A、a>0 B、a=0 C、c>0 D、c=0二、填空题(共6小题,每小题4分,满分24分)
-
13. 分解因式:x2﹣4= .14. 若二次根式 在实数范围内有意义,则x的取值范围是 .
15. 已知四个点的坐标分别是(﹣1,1),(2,2),( , ),(﹣5,﹣ ),从中随机选取一个点,在反比例函数y= 图象上的概率是 .16.如图所示的两段弧中,位于上方的弧半径为r上 , 下方的弧半径为r下 , 则r上r下 . (填“<”“=”“<”)
 17. 若x+y=10,xy=1,则x3y+xy3的值是 .18.
17. 若x+y=10,xy=1,则x3y+xy3的值是 .18.如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是 .

三、解答题(共9小题,满分90分)
-
19. 计算:|﹣1|﹣ +(﹣2016)0 .20. 化简:a﹣b﹣ .21.
一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:∠BAC=∠DAC.
 22. 列方程(组)解应用题:
22. 列方程(组)解应用题:某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,甲乙两种票各买了多少张?
23.福州市2011﹣2015年常住人口数统计如图所示.
根据图中提供的信息,回答下列问题:
 (1)、福州市常住人口数,2015年比2014年增加了万人;
(1)、福州市常住人口数,2015年比2014年增加了万人;
(2)、与上一年相比,福州市常住人口数增加最多的年份是;
(3)、预测2016年福州市常住人口数大约为多少万人?请用所学的统计知识说明理由.24.如图,正方形ABCD内接于⊙O,M为 中点,连接BM,CM.
 (1)、求证:BM=CM;(2)、当⊙O的半径为2时,求 的长.
(1)、求证:BM=CM;(2)、当⊙O的半径为2时,求 的长.
25.如图,在△ABC中,AB=AC=1,BC= ,在AC边上截取AD=BC,连接BD.
 (1)、通过计算,判断AD2与AC•CD的大小关系;(2)、求∠ABD的度数.
(1)、通过计算,判断AD2与AC•CD的大小关系;(2)、求∠ABD的度数.
