初中数学浙教版七年级上学期期末冲刺满分专题5 一元一次方程综合题

试卷更新日期：2020-11-29 类型：复习试卷

进入出卷网下载

一、计算题

1.

(1)、计算： $| - 2 | + \sqrt{4} - {(- 1)}^{2}$ ；

(2)、解方程： $4 x - 3 = 2 (x - 1)$ .

查看试题解析
2. 解方程： $\frac{2 x - 1}{3} - \frac{4 x + 1}{5} = 2$

查看试题解析
3. 解下列方程：

(1)、x-7=10 - 4（x+0.5）

(2)、 $\frac{x - 1}{2} - \frac{3 + 2 x}{3} = 1$ .

查看试题解析
4.

(1)、2（x﹣2）﹣3（4x﹣1）＝9（1﹣x）；

(2)、 $\frac{2 x - 1}{3} - \frac{5 x + 2}{6} = \frac{1 - 2 x}{2} - 2$ ．

查看试题解析

二、解答题

5. 已知关于x的方程 $\frac{1}{2}$ （2x+3）﹣3x＝ $\frac{3}{2}$ 和3x+2m＝6x+1的解相同，求：代数式（﹣2m）²⁰²⁰﹣（m﹣ $\frac{3}{2}$ ）²⁰¹⁹的值．

查看试题解析
6. 小明每天早上要在7：50之前赶到距家900米的学校上学.小明以60米/分的速度出发10分后，小明的爸爸发现他忘了带语文书.于是，爸爸立即以160米/分的速度去追小明，爸爸能否在小明进学校前追上他？若能，请说明理由，若不能，请计算，爸爸的速度至少为多少时才能赶在小明进学校前追上他？

查看试题解析
7. 如图，在数轴上有A、B、C三点，A、B两点所表示的有理数分别是2k-4和-2k+4，且k为最大的负整数．点C在A、B之间，且C到B的距离是到A点距离的2倍，动点P从点A出发，以每秒3个单位长度的速度向右运动，到达点B后立即返回，以每秒3个单位长度的速度向左运动；动点Q从点C出发，以每秒l个单位长度的速度向右运动，设它们同时出发，运动时间为t秒，当点P与点Q第二次重合时，P、Q两点停止运动，

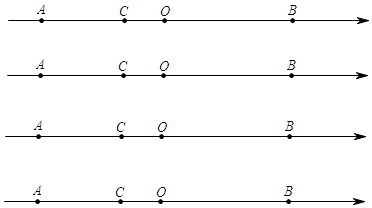(1)、直接写出A、B、C三点所代表的数值；A：B：C：

(2)、当t为何值时，P到点A与点Q的距离相等；

(3)、当t为何值时，P、Q两点间的距离为1个单位长度．

查看试题解析
8.
【定义】：在同一直线上的三点A、B、C，若满足点C到另两个点A、B的距离具有2倍关系，则我们就称点C是其余两点的强点 $($ 或弱点 $) .$ 具体地：

①当点C在线段AB上时，若 $C A = 2 C B$ ，则称点C是【A，B】的强点；若 $C B = 2 C A$ ，则称点C是【B，A】的强点；

②当点C在线段AB的延长线上时，若 $C A = 2 C B$ ，则称点C是【A，B】的弱点；

【例如】如图，数轴上点A、B、C、D分别表示数 $- 1$ 、2、1、0，则点C是【A，B】的强点，又是【A，D】的弱点；点D是【B，A】的强点，又是【B，C】的弱点；

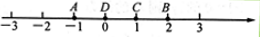
【应用】Ⅰ.如图，M、N为数轴上两点，点M所表示的数为 $- 2$ ，点N所表示的数为4．

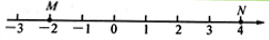
【M，N】的强点表示的数为．

【N，M】的弱点表示的数为．

Ⅱ.如图，数轴上，点A所表示的数为 $- 20$ ，点B所表示的数为 $40.$ 一只电子蚂蚁P从点B出发，以4个单位每秒的速度沿数轴向左运动，设运动时间为t秒 $.$

$①$ 求当t为何值时？P是【B，A】的弱点．

$②$ 求当t为何值时？P、A、B三个点中恰有一个点为其余两点的强点．

查看试题解析
9. 在数轴上，点A，B，C表示的数分别是－6，10，12．点A以每秒3个单位长度的速度向右运动，同时线段BC以每秒1个单位长度的速度也向右运动．

(1)、运动前线段AB的长度为；

(2)、当运动时间为多长时，点A和线段BC的中点重合？

(3)、试探究是否存在运动到某一时刻，线段AB= $\frac{1}{2} A C$ ？若存在，求出所有符合条件的点A表示的数；若不存在，请说明理由．

查看试题解析
10. 如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示﹣10，点B表示10，点C表示18，我们称点A和点C在数轴上相距28个长度单位．动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒．问：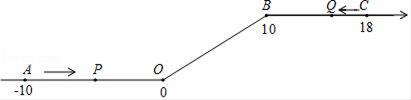

(1)、动点P从点A运动至C点需要多少时间？

(2)、P、Q两点相遇时，求出相遇点M所对应的数是多少；

(3)、求当t为何值时，P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等．

查看试题解析
11. 甲、乙两商场以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费．设小红在同一商场累计购物x元，其中x>100.

(1)、根据题意，填写下表(单位：元)：

(2)、当x取何值时，小红在甲、乙两商场的实际花费相同？

(3)、当小红在同一商场累计购物超过100元时，在哪家商场的实际花费少？

查看试题解析
12. $2020$ 年 $5$ 月份，省城太原开展了“活力太原·乐购晋阳”消费暖心活动，本次活动中的家电消费券单笔交易满 $600$ 元立减 $128$ 元（每次只能使用一张）某品牌电饭煲按进价提高 $50 %$ 后标价，若按标价的八折销售，某顾客购买该电饭煲时，使用一张家电消费券后，又付现金 $568$ 元．求该电饭煲的进价．

查看试题解析
13. 某爱心社给甲、乙两所学校捐赠图书，已知捐给甲校的图书数量和捐给乙校的图书数量之比为3∶2，且捐给甲校的图书数量比捐给乙校的2倍少700本，求捐给甲、乙两所学校的图书各是多少本？

查看试题解析
14. 如图，A，O，B三点在一条直线上， $∠ AOC$ =3 $∠ COD$ ，OE平分 $∠ BOD$ ， $∠ COE$ =80 $°$ ，求 $∠ COD$ 的度数.

查看试题解析

三、综合题

15. 试根据图中信息，解答下列问题.

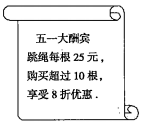(1)、一次性购买6根跳绳需元，一次性购买12根跳绳需元；

(2)、小红比小明多买2根，付款时小红反而比小明少5元，你认为有这种可能吗？若有，请求出小红购买跳绳的根数；若没有，请说明理由.

查看试题解析
16. 已知数轴上有A、B、C三点，分别表示有理数－26，－10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒.

(1)、用含t的代数式表示P到点A和点C的距离：PA= ， PC=。

(2)、当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，当点P运动到点C时，P、Q两点运动停止，
①当P、Q两点运动停止时，求点P和点Q的距离；

②求当t为何值时P、Q两点恰好在途中相遇.

查看试题解析

17. 自2016年1月1日起，某市居民生活用水实施年度阶梯水价，具体水价标准见下表：

类别	水费价格（元/立方米）	污水处理费（元/立方米）	综合水价（元/立方米）
第一阶梯≤120（含）立方米	3.5	1.5	5
第二阶梯120～180（含）立方米	5.25	1.5	6.75
第三阶梯＞180立方米	10.5	1.5	12

例如，某户家庭年用水124立方米，应缴纳水费：120x5+（124﹣120）x6.75＝627（元）.

(1)、小华家2017年共用水150立方米，则应缴纳水费多少元？

(2)、小红家2017年共用水m立方米（m＞200），请用含m的代数式表示应缴纳的水费.

(3)、小刚家2017年，2018年两年共用水360立方米，已知2018年的年用水量少于2017年的年用水量，两年共缴纳水费2115元，求小刚家这两年的年用水量分别是多少？

查看试题解析

18. 某垃圾处理厂，对不可回收垃圾的处理费用为90元/吨，可回收垃圾的分拣处理费用也为90元/吨，分拣后再被相关企业回收，回收价格如下表：

垃圾种类	纸类	塑料类	金属类	玻璃类
回收单价(元/吨)	500	800	500	200

据了解，可回收垃圾占垃圾总量的60%，现有A，B，C三个小区12月份产生的垃圾总量分别为100吨，100吨和m吨。

(1)、已知A小区金属类垃圾质量是塑料类的5倍，纸类垃圾质量是塑料类的2倍。设塑料类的质量为x吨，则A小区可回收垃圾有吨，其中玻璃类垃圾有吨(用含x的代数式表示)

(2)、B小区纸类与金属类垃圾总量为35吨，当月可回收垃圾回收总金额扣除所有垃圾处理费后，收益16500元，求12月份该小区可回收垃圾中塑料类垃圾的质量。

(3)、C小区发现塑料类与玻璃类垃圾的回收总额恰好相等，所有可回收垃圾的回收总金额为12000元，设该小区塑料类垃圾质量为a吨，求a与m的数量关系。

查看试题解析

19. 已知线段AB＝30cm

(1)、如图1，点P沿线段AB自点A向点B以2cm/s的速度运动，同时点Q沿线段点B向点A以3cm/s的速度运动，几秒钟后，P、Q两点相遇？

(2)、如图1，几秒后，点P、Q两点相距10cm？

(3)、如图2，AO＝4cm，PO＝2cm，当点P在AB的上方，且∠POB＝60°时，点P绕着点O以30度/秒的速度在圆周上逆时针旋转一周停止，同时点Q沿直线BA自B点向A点运动，假若点P、Q两点能相遇，求点Q的运动速度．

查看试题解析
20. 如图，已知射线OB平分∠AOC，∠AOC的余角比∠BOC小42°.

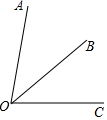(1)、求∠AOB的度数：

(2)、过点O作射线OD，使得∠AOC＝4∠AOD，请你求出∠COD的度数

(3)、在（2）的条件下，画∠AOD的角平分线OE，则∠BOE＝.

查看试题解析
21. 如图，点O为原点，A、B为数轴上两点，点A表示的数a，点B表示的数是b，且 $| a b + 32 | + {(b - 4)}^{2} = 0$ .

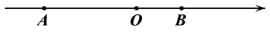(1)、a= ， b=；

(2)、在数轴上是否存在一点P，使 $P A - P B = 2 O P$ ，若有，请求出点P表示的数，若没有，请说明理由？

(3)、点M从点A出发，沿 $A \to O \to A$ 的路径运动，在路径 $A \to O$ 的速度是每秒2个单位，在路径 $O \to A$ 上的速度是每秒4个单位，同时点N从点B出发以每秒3个单位长向终点A运动，当点M第一次回到点A时整个运动停止.几秒后MN=1？

查看试题解析

22. 2018年元旦期间，某商场打出促销广告，如下表所示：

优惠条件	一次性购物不超过200元	一次性购物超过200元，但不超过500元	一次性购物超过500元
优惠办法	没有优惠	全部按九折优惠	其中500元仍按九折优惠，超过500元部分按八折优惠

(1)、用代数式表示（所填结果需化简）

设一次性购买的物品原价是x元，当原价x超过200元但不超过500元时，实际付款为元；当原价x超过500元时，实际付款为元；

(2)、若甲购物时一次性付款490元，则所购物品的原价是多少元？

(3)、若乙分两次购物，两次所购物品的原价之和为1000元（第二次所购物品的原价高于第一次），两次实际付款共894元，则乙两次购物时，所购物品的原价分别是多少元？

查看试题解析

23. 如图，已知数轴上点A表示的数为﹣7，点B是数轴上位于点A右侧一点，且AB＝30.动点P从点A出发，以每秒3个单位长度的速度沿数轴向点B方向匀速运动，设运动时间为t秒.

(1)、数轴上点B表示的数为；点P表示的数为（用含t的代数式表示）.

(2)、动点Q从点B出发，以每秒2个单位长度的速度沿数轴向点A方向匀速运动；点P、点Q同时出发，当点P与点Q相遇后，点P马上改变方向，与点Q继续向点A方向匀速运动（点P、点Q在运动过程中，速度始终保持不变）；当点P返回到达A点时，P、Q停止运动.设运动时间为t秒.
①当点P返回到达A点时，求t的值，并求出此时点Q表示的数.

②当点P是线段AQ的三等分点时，求t的值.

查看试题解析
24. 周末，小明和爸爸在400米的环形跑道上骑车锻炼，他们在同一地点沿着同一方向同时出发，骑行结束后两人有如下对话：

(1)、他们的对话内容，求小明和爸爸的骑行速度，

(2)、一次追上小明后，在第二次相遇前，再经过多少分钟，小明和爸爸相距50m？

查看试题解析
25. 已知a是最大的负整数，b是-5的相反数，c= $- | - 3 |$ ，且a、b、c分别是点A、B、C在数轴上对应的数.若动点P从点A出发沿数轴正方向运动，动点Q同时从点B出发也沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒1个单位长度.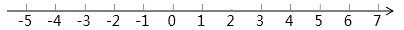

(1)、求a、b、c的值；

(2)、P、Q同时出发，求运动几秒后，点P可以追上点Q？

(3)、在（2）的条件下，P、Q出发的同时，动点M从点C出发沿数轴正方向运动，速度为每秒6个单位长度，点M追上点Q后立即返回沿数轴负方向运动，追上后点M再运动几秒，M到Q的距离等于M到P距离的两倍？

查看试题解析
26. 已知数轴上A，B两点对应的数分别为-2和8，P为数轴上一点，对应的数为x ．

(1)、线段PA的长度可表示为（用含x的式子表示）；

(2)、在数轴上是否存在点P，使得PA-PB=6？若存在，求出x的值；若不存在，请说明理由；

(3)、当P为线段AB的中点时，点A，B，P同时开始在数轴上分别以每秒3个单位长度，每秒2个单位长度，每秒1个单位长度沿数轴正方向运动，试问经过几秒，PB=2PA？

查看试题解析