初中数学浙教版七年级上学期期末冲刺满分专题4 代数式综合题
试卷更新日期:2020-11-29 类型:复习试卷
一、计算题
-
1.2. 计算:3. 先化简,再求值: ,其中 .4.5.6. 先化简,再求值.(1)、 .其中 , .(2)、已知 , ,当 时,求: 的值.
二、解答题
-
7. 已知a,b互为倒数,c,d互为相反数, ,求代数式 的值,8. 利民商店出售一种商品原价为a,有如下几种方案:
(1)先提价10%,再降价10%;(2)先降价10%,再提价10%;(3)先提价20%,再降价20%。问用这三种方案调价的结果是否一样?最后是不是都恢复了原价?
三、综合题
-
9. 已知长方形长为(2a+5)米,宽为(2a+1)米,它的周长与一个正方形周长相等.(1)、求这个正方形的边长.(2)、设这个长方形的面积为M,正方形的面积为N,试比较M、N的大小.10. 今年“十、一”黄金周期间,舒城丰乐生态园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数变化
单位:千人
+1.6
+0.8
+0.4
-0.4
-0.8
+0.2
-1.2
(1)、若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客人数?(2)、请判断七天内游客人数最多的是哪天?请说明理由.(3)、若9月30日的游客人数为5千人,门票每人10元.问黄金周期间舒城丰乐生态园门票收入是多少元?11. 请同学们仔细阅读下列步骤,完成问题:①任意写一个三位数,百位数字比个位数字大2;
②交换百位数字与个位数字,得到一个三位数;
③用上述的较大的三位数减去较小的三位数,所得的差为三位数;
④交换这个差的百位数字与个位数字又得到一个三位数;
⑤把③④中的两个三位数相加,得到最后结果.
问题:
(1)、③中的三位数是;④中的三位数是;⑤中的结果是 .(2)、在草稿纸上试一个不同的三位数,看看结果是否都一样?如果一样,请你用含a、b的代数式表示这个三位数,解释其中的原因.12. 一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接. (1)、若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(1)、若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)、若用餐的人数有90人,则需要这样的餐桌多少张?
13. 某校计划购买20张书柜和一批书架,现从A、B两家超市了解到:同型号的产品价格相同,书柜每张210元,书架每个70元.A超市的优惠政策为每买一张书柜赠送一个书架,B超市的优惠政策为所有商品打8折出售.设该校购买x(x>20)个书架.(1)、若该校到同一家超市选购所有书柜和书架,则到A超市需准备元货款,到B超市需准备元货款;(用含x的式子表示)(2)、若规定只能到其中一家超市购买所有书柜和书架,当购买多少个书架时,无论到哪家超市购买所付货款都一样?(3)、若该校想购买20张书柜和100个书架,且可到两家超市自由选购,你认为至少需准备多少元货款, 并说明理由.14. 在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:功率
使用寿命
价格
普通白帜灯
100瓦(即0.1千瓦)
2000小时
3元/盏
优质节能灯
20瓦(即0.02千瓦)
4000小时
35元/盏
已知这两种灯的照明效果一样,小明家所在地的电价是每度0.5元.
(注:用电度数=功率(千瓦)×时间(小时),费用=灯的售价+电费)
请你解决以下问题:
(1)、如果选用一盏普通白炽灯照明1000小时,那么它的费用是多少?(2)、在白炽灯的使用寿命内,设照明时间为x小时,请用含x的式子分别表示用一盏白炽灯的费用和一盏节能灯的费用;(3)、照明多少小时时,使用这两种灯的费用相等?(4)、如果计划照明4000小时,购买哪一种灯更省钱?请你通过计算说明理由.15. 窗户的形状如图所示(图中长度单位:cm),其中上部是半圆形,下部是边长相同的四个小正方形. 已知下部小正方形的边长是acm.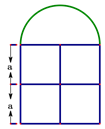 (1)、计算窗户的面积(计算结果保留π).(2)、计算窗户的外框的总长(计算结果保留π).(3)、安装一种普通合金材料的窗户单价是175元/平方米,当a=50cm时,请你帮助计算这个窗户安装这种材料的费用(π≈3.14,窗户面积精确到0.1).16. 将自然数按照下表进行排列:
(1)、计算窗户的面积(计算结果保留π).(2)、计算窗户的外框的总长(计算结果保留π).(3)、安装一种普通合金材料的窗户单价是175元/平方米,当a=50cm时,请你帮助计算这个窗户安装这种材料的费用(π≈3.14,窗户面积精确到0.1).16. 将自然数按照下表进行排列: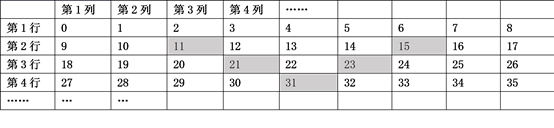
用 表示第 行第 列数,例如 表示第4行第3列数是29.)
(1)、已知 , , ;(2)、将图中5个阴影方格看成一个整体并在表格内平移,所覆盖的5个自然数之和能否为2021?若能,求出这个整体中左上角最小的数;若不能,请说明理由;(3)、用含 的代数式表示 .17. 已知代数式ax5+bx3+3x+c“当x=0时,该代数式的值为-1。(1)、求c的值;(2)、已知当x=1时.该代数式的值为-1,试求a+b+c的值;(3)、已知当x=3时,该代数式的值为9,试求当x=-3时该代数式的值。18. 为给同学们创造更好的读书条件,学校准备新建一个长度为L的读书长廊,并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起,按如图所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.6m.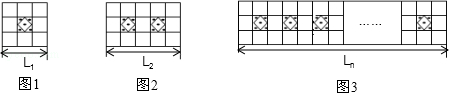 (1)、按图示规律,第一图案的长度L1=m;第二个图案的长度L2=m.(2)、请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln之间的关系.(3)、当走廊的长度L为36.6m时,请计算出所需带有花纹图案的瓷砖的块数.19. 新学期,两摞规格相同准备发放的数学课本整齐地叠放在讲合上,请根据图中所给出的数据信息,解答下列问题:
(1)、按图示规律,第一图案的长度L1=m;第二个图案的长度L2=m.(2)、请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln之间的关系.(3)、当走廊的长度L为36.6m时,请计算出所需带有花纹图案的瓷砖的块数.19. 新学期,两摞规格相同准备发放的数学课本整齐地叠放在讲合上,请根据图中所给出的数据信息,解答下列问题: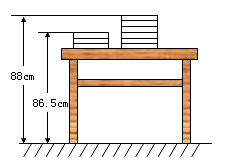 (1)、设课本数 (本),请写出整齐叠放在桌面上的数学课本距离地面的高度的代数式(用含 的代数式表示);(2)、桌面上有56本与题(1)中相同的数学课本,整齐叠放成一摞,若从中取走14本,求余下的数学课本距离地面的高度.20. 某国际化学校实行小班制教学,七年级四个班共有学生(6m-3n)人,一班有学生m人,二班人数比一班人数的两倍少n人,三班人数比二班人数的一半多12人.(1)、求三班的学生人数(用含m.n的式子表示);(2)、求四班的学生人数;(用含m.n的式子表示) ;(3)、若四个班共有学生120人,求二班比三班多的学生人数?21. 2019国庆期间,据统计,我市武功山接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
(1)、设课本数 (本),请写出整齐叠放在桌面上的数学课本距离地面的高度的代数式(用含 的代数式表示);(2)、桌面上有56本与题(1)中相同的数学课本,整齐叠放成一摞,若从中取走14本,求余下的数学课本距离地面的高度.20. 某国际化学校实行小班制教学,七年级四个班共有学生(6m-3n)人,一班有学生m人,二班人数比一班人数的两倍少n人,三班人数比二班人数的一半多12人.(1)、求三班的学生人数(用含m.n的式子表示);(2)、求四班的学生人数;(用含m.n的式子表示) ;(3)、若四个班共有学生120人,求二班比三班多的学生人数?21. 2019国庆期间,据统计,我市武功山接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):日期
1日
2日
3日
4日
5日
6日
7日
人数变化
(万人)
+2.8
+1.9
-0.3
-0.1
+0.8
-0.2
-1.7
(1)、若2019年9月30日我市武功山的游客人数为a万人,则10月1日的游客人数为万人;七天内游客人数最大的是10月日;(2)、若2019年9月30日游客人数是2万人,求这一年我市武功山黄金周7天平均每天游客是多少人?(3)、在(2)的基础上,每人平均每天消费200元,则我市武功山在2019年国庆期间的总营业额为多少万元?22. 用三角形和六边形按如图所示的规律拼图案. (1)、第4个图案中,三角形有个,六边形有个;(2)、第n(n为正整数)个图案中,三角形与六边形各有多少个?(3)、第2019个图案中,三角形与六边形共有多少个?(4)、是否存在某个符合上述规律的图案,其中有100个三角形与48个六边形?如果有,指出是第几个图案;如果没有,说明理由.23.(1)、请按“24点”的游戏规则(每个数只字能用依次进行加、减、乘、除或乘方运算),请在下列两组数中选择一组数运算得24,写出算式.
(1)、第4个图案中,三角形有个,六边形有个;(2)、第n(n为正整数)个图案中,三角形与六边形各有多少个?(3)、第2019个图案中,三角形与六边形共有多少个?(4)、是否存在某个符合上述规律的图案,其中有100个三角形与48个六边形?如果有,指出是第几个图案;如果没有,说明理由.23.(1)、请按“24点”的游戏规则(每个数只字能用依次进行加、减、乘、除或乘方运算),请在下列两组数中选择一组数运算得24,写出算式.① -1,6,8,4;② 5,7,3,-6 .
解:选择__▲_;
算式:_▲.
(2)、已知x、y互为相反数,a、b互为倒数,m的绝对值为3,求代数式 4(x+y)-ab+m3的值).24. 如图所示,某公司打算将一长方形空地美化,并在一边修一个半圆花坛,其余部分(图中阴影部分)种草.已知长方形的长为 米,宽为 米,半圆半径为 米.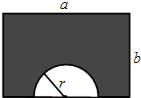 (1)、用代数式表示阴影部分的面积.(结果保留 )(2)、当 时,请问阴影部分的面积为多少平方米?(3)、如果种草的每平方米花费100元,修建花坛每平方米花费200元,求该公司美化空地的总费用.(用含 , , , 的式子表示)25. 观察下面的三行单项式
(1)、用代数式表示阴影部分的面积.(结果保留 )(2)、当 时,请问阴影部分的面积为多少平方米?(3)、如果种草的每平方米花费100元,修建花坛每平方米花费200元,求该公司美化空地的总费用.(用含 , , , 的式子表示)25. 观察下面的三行单项式x,2x2 , 4x3 , 8x4 , 16x5…①
﹣2x,4x2 , ﹣8x3 , 16x4 , ﹣32x5…②
2x,﹣3x2 , 5x3 , ﹣9x4 , 17x5…③
根据你发现的规律,完成以下各题:
(1)、第①行第8个单项式为;第②行第2020个单项式为.(2)、第③行第n个单项式为.(3)、取每行的第9个单项式,令这三个单项式的和为A.计算当x= 时,256(A+ )的值.26. 一般情况下,“ ”并不成立,但当 , 取某些数时,可以使它成立,例如 .我们称能使“ ”成立的数对 , 为“优数对”,记为( , ).(1)、若( , )是一个“优数对”,求 的值;(2)、请你写出一个“优数对”( , ),其中 ,且 ;(3)、若( , )是一个“优数对”,求代数式 的值.27. 如图是用长度相等的小棒按一定规律摆成的一组图案.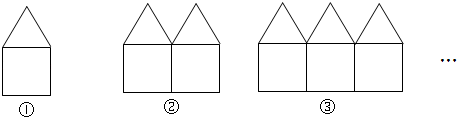 (1)、第1个图案中有6根小棒;第2个图案中有根小棒;第3个图案中有根小棒;(2)、第n个图案中有多少根小棒?(3)、第25个图案中有多少根小棒?(4)、是否存在某个符合上述规律的图案,由2032根小棒摆成?如果有,指出是滴几个图案;如果没有,请说明理由.
(1)、第1个图案中有6根小棒;第2个图案中有根小棒;第3个图案中有根小棒;(2)、第n个图案中有多少根小棒?(3)、第25个图案中有多少根小棒?(4)、是否存在某个符合上述规律的图案,由2032根小棒摆成?如果有,指出是滴几个图案;如果没有,请说明理由.