初中数学浙教版七年级上学期期末冲刺满分专题2 有理数的运算综合题

试卷更新日期：2020-11-28 类型：复习试卷

进入出卷网下载

一、计算题

1. 计算：

(1)、23-17-（-7）+（-13）

(2)、 $24 \times (- \frac{5}{6} + \frac{1}{8} + \frac{3}{4})$

(3)、 $(- 5) \times (- 4) + 3 \times (- 2)$

(4)、 ${(- 1)}^{4} + (1 - \frac{1}{2}) \div 3 \times (4 + 2^{3})$

查看试题解析
2. 计算：

(1)、（﹣8）﹣（+8）﹣（﹣10）

(2)、﹣54×2 $\frac{1}{4}$ ÷（﹣4 $\frac{1}{2}$ ）× $\frac{2}{9}$

(3)、﹣24×（ $\frac{1}{3} - \frac{3}{4} + \frac{1}{6}$ ）

(4)、﹣4×（﹣8 $\frac{8}{9}$ ）+（﹣8）×（﹣8 $\frac{8}{9}$ ）+12×（﹣8 $\frac{8}{9}$ ）

(5)、 $- 1^{4} - [1 - (1 - 0.5 \times \frac{1}{3}) \times 6]$

查看试题解析
3. 计算：

(1)、 $- 7 + 13 - 6 + 20$

(2)、 $1 + (- \frac{4}{7}) - (- \frac{1}{5}) - \frac{3}{7} + \frac{9}{5}$

(3)、－81÷（－ $\frac{1}{4}$ ）× $\frac{4}{9}$ ÷（－16）

(4)、 $- 24 \times (- \frac{1}{2} + \frac{3}{4} - \frac{1}{3})$

(5)、8﹣（﹣2）²×（﹣3）﹣（﹣5）²

(6)、 $- 1^{4} \div (- \frac{3}{10}) \times \frac{1}{25} - | 0.8 - 1 |$

查看试题解析

二、解答题

4. 设 A 是由 2×4 个整数组成的 2 行 4 列的数表，如果某一行（或某一列）各数之和为负数，则改变该行（或该列）中所有数的符号，称为一次“操作”．数表A 如下表所示，如果经过两次“操作”，使得到的数表每行的各数之和与每列的各数之和均为非负整数，请写出每次“操作”后所得的数表．（写出一种方法即可）

1

2

3

－7

－2

－1

0

1

查看试题解析
5. 已知 $m, n$ 互为相反数，且 $m \neq n, p, q$ ，互为倒数， $a$ 的绝对值为6.求 $a (m + n) + 2 p q - \frac{1}{2} a - \frac{m}{n}$ 的值.

查看试题解析
6. 已知b的倒数与a互为相反数，c，d互为倒数，m的绝对值为4，求5（a+ $\frac{1}{b} -$ 2）+6cd﹣7m的值.

查看试题解析
7. 已知 $| a - 3 | = 4$ ， $| b + 2 | = 1$ ，求a与b的乘积．

查看试题解析
8. 一天，甲乙两人利用温差测量山峰的高度，甲在山顶测得温度是-1℃，乙此时在山脚测得温度是5℃，已知该地区每增加100米，气温大约降低0.6℃，这个山峰的高度大约是多少米？

查看试题解析
9. 一场游戏规则如下：
（ 1 ）每人每次抽4张卡片，如果抽到形如的卡片，那么加上卡片上的数字，如果抽到形如的卡片，那么减去卡片上的数字；

（ 2 ）比较两人所抽到的4张卡片的计算结果，结果大的为胜者.

请你通过计算（要求有计算过程）回答本次游戏获胜的是谁？

小亮抽到的卡片如图所示：

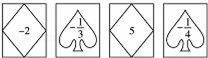小丽抽到的卡片如图所示：

查看试题解析

10. 下表是某班5名同学某次数学测试成绩.根据信息完成下表，并回答问题.

五人中分数最高的是谁？分数最低的是谁？谁的分数与全班平均分最接近？

姓名

王芳

刘兵

张昕

李聪

江文

成绩

与全班平

均分之差

－1

－2

查看试题解析

11. 有个写运算符号的游戏：在“3□（2□3）□ $\frac{4}{3}$ □2” 中的每个□内，填入+，-，×，÷中的某一个（可重复使用），然后计算结果．

(1)、请计算琪琪填入符号后得到的算式： $3 \times (2 \div 3) - \frac{4}{3} \div 2^{2}$ ；

(2)、嘉嘉填入符号后得到的算式是 $3 \div (2 \times 3) \times \frac{4}{3}$ □ $2^{2}$ ，一不小心擦掉了□里的运算符号，但她知道结果是 $- \frac{10}{3}$ ，请推算□内的符号．

查看试题解析
12. 已知：有理数m所表示的点与﹣1表示的点距离4个单位，a，b 互为相反数，且都不为零，c，d互为倒数．求：2a+2b+（ $\frac{a}{b}$ ﹣3cd)﹣m的值．

查看试题解析
13. 如图所示，小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各题：

(1)、若从中抽出2张卡片，且这2个数字的差最小，应如何抽取？最小值是多少？

(2)、若从中抽出2张卡片，且这2个数字的积最大，应如何抽取？最小值是多少？

(3)、若从中抽出4张卡片，运用加、减、乘、除、乘方、括号等运算符号，使得结果为24.请写出运算式.（只需写出一种）

查看试题解析

三、作图题

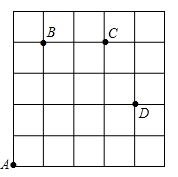
14. 如图，小虫在 $5 \times 5$ 的方格（每小方格边长为1cm）上沿着网格线运动.小虫从A处出发去寻找B、C、D处的其他虫虫，规定：向上向右走为正，向下向左走为负.如果从A到B记为： $A \to B (+ 1 ， + 4)$ ，从B到A记为： $B \to A (- 1 ， - 4)$ ，其中第一个数表示左右方向，第二个数表示上下方向，那么图中

(1)、 $A \to D$ ； $D \to B$ ；

(2)、若小虫的行走路线为 $A \to B \to C \to D$ ，请计算小虫走过的路程；

(3)、若小虫从A处去寻找大虫，它的行走路线依次为(＋1，＋2)，(＋3，－1)，(—2，＋2)，请在图中标出大虫的位置E点.

查看试题解析
15. 一辆货车从仓库O出发在东西街道上运送水果，规定向东为正方向，一次到达的5个销售地点依次分别为A，B，C，D，E，最后回到仓库O，货车行驶的记录（单位：千米）如下：+1，+3，﹣6，﹣1，﹣2，+5.请问：

(1)、请以仓库O为原点，向东为正方向，选择适当的单位长度，画出数轴，并标出A，B，C，D，E的位置；

(2)、试求出该货车共行驶了多少千米？

(3)、如果货车运送的水果以100千克为标准重量，超过的千克数记为正数，不足的千克数记为负数，则运往A，B，C，D，E五个地点的水果重量可记为：
+50，﹣15，+25，﹣10，﹣15，则该货车运送的水果总重量是多少千克？

查看试题解析
16. 如图，一辆货车从超市出发，向东走了3千米到达小颖家，继续走了2千米到达小亮家，然后向西走了9.5千米到达小明家，最后回到超市.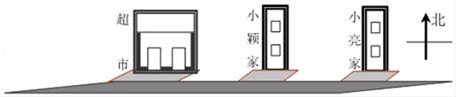

(1)、以超市为原点，以向东方向为正方向，用1个单位长度表示1千米，请你画出数轴，并在数轴上表示出小颖、小亮、小明家的位置；

(2)、小明家距小颖家多远？

(3)、货车一共行驶了多少千米？

查看试题解析

四、综合题

17. 某快递公司的快递员小李骑摩托车从公司M处向西行驶了3km到达A地送货后，继续向西行驶1km到达B地送货，接着向东行驶了9km到达C地送货，然后又继续向东行驶了2km到达D处家的位置．

(1)、以公司为原点，向东为正方向画出数轴，并在数轴上标出A、B、C、D的位置；

(2)、公司距离他家多远？

(3)、若每千米用油0.08升，则小李本次出发共用油多少升？

查看试题解析
18. 小明早晨跑步，他从自家向东跑了2千米到达小彬家，继续向东跑了1.5千米到达小红家，然后向西跑了4.5千米到达中心广场，最后回到家.

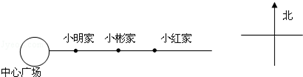(1)、以小明家为原点，以向东的方向为正方向，用1 个单位长度表示1千米，在数轴上表示出中心广场，小彬家和小红家的位置？

(2)、小彬家距中心广场多远？

(3)、小明一共跑了多少千米？

查看试题解析

19. 某自行车厂一周计划生产1400辆自行车，平均每天生产自行车200辆，由于各种原因，实际每天生产量与计划每天生产量相比有出入.下表是某周的自行车生产情况（超计划生产量为正、不足计划生产量为负，单位：辆）：

星期	一	二	三	四	五	六	日
增减	+5	﹣2	﹣4	+13	﹣10	+16	﹣9

(1)、根据记录可知前三天共生产自行车辆；

(2)、产量最多的一天比产量最少的一天多生产辆；

(3)、若该厂实行按生产的自行车数量的多少计工资，即计件工资制.如果每生产一辆自行车可得人民币60 元，那么该厂工人这一周的工资总额是多少元？

查看试题解析

20. 对于任意四个有理数 $a ， b ， c ， d$ ，我们规定： $(a ， b) ★ (c ， d) = b c - a d$ ，例如： $(1 ， 2) ★ (3 ， 4) = 2 \times 3 - 1 \times 4 = 2$ ，根据上述规定解决下列问题：

(1)、计算 $(3 ， - 5) ★ (5 ， - 3)$ ；

(2)、若有理数对 $(- 2 ， 2 x - 1) ★ (1 ， x + 1) = 25$ ，求 $x$ 的值.

查看试题解析
21.

(1)、小明爸爸上周买进某种股票1000股，每股27.3元，下表为本周每天该股票的涨跌情况：

星期

一

二

三

四

五

每股涨跌

+1

+1.5

﹣1.5

﹣2.5

+0.5

①星期三收盘时，每股是多少元？

②本周内最高价是每股多少元？最低价是每股多少元？

③若小明爸爸按本周五的收盘价将股票全部卖出，你认为他会获利吗？

(2)、国家规定个人发表文章、出版图书所得稿费的纳税计算方法是：
①稿费不高于800元的不纳税：

②稿费高于800元，而低于4000元的应缴纳超过800元的那部分稿费的14%的税；

③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税；

若王老师获得稿费后纳税420元，求这笔稿费是多少钱？

查看试题解析
22. 如图：在数轴上A点表示数 $a$ ，B点示数 $b$ ，C点表示数 $c$ ， $b$ 是最小的正整数，且 $a$ 、 $c$ 满足 $| a + 3 | + {(c - 9)}^{2} = 0$ ．

(1)、 $a$ = ， $b$ = ， $c$ =；

(2)、若将数轴折叠，使得A点与C点重合，则点B与数表示的点重合；

(3)、若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动，假设 $t$ 秒钟过后，A、B、C三点中恰有一点为另外两点的中点，求 $t$ 的值；

(4)、若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动时，小聪同学发现：当点C在B点右侧时， $m \cdot$ BC+3AB的值是个定值，求此时 $m$ 的值．

查看试题解析
23. 学习有理数的乘法后，老师给同学们这样一道题目：计算：49 $\frac{24}{25}$ ×（-5），看谁算的又快又对，有两位同学的解法如下：
聪聪；原式=- $\frac{1249}{25}$ ×5=- $\frac{1249}{5}$ -249 $\frac{4}{5}$ ；

明明：原式=（49+ $\frac{24}{25}$ ）×（-5）=49×（-5）+ $\frac{24}{25}$ ×（-5）=-249 $\frac{4}{5}$ ，

(1)、对于以上两种解法，你认为谁的解法较好？

(2)、上面的解法对你有何启发，你认为还有更好的方法吗？如果有，请把它写出来；

(3)、用你认为最合适的方法计算：39 $\frac{15}{16}$ ×（-8）.

查看试题解析

24. 一辆公共汽车从起点站开出后，途中经过6个停靠站，最后到达终点站，下表记录了这辆公共汽车全程载客变化情况（上车为正，下车为负）。

停靠站

起点站

中间第1站

中间第2站

中间第3站

中间第4站

中间第5站

中间第6站

终点站

上下车

情况

+21

-3

-4

-7

-9

-7

-12

(1)、中间第4站上车人数是人，下车人数是人;

(2)、中间的6个站中，第站没有人上车，第站没有人下车;

(3)、公共汽车到中间第2站后，开车时车上有多少名乘客？离开第4站时车上有多少名乘客？

查看试题解析

25. 某校初2021届1到4班计划每班购买数量相同的图书布置班级读书角，但是由于种种原因，实际购书量与计划有出入，下表是实际购书情况：

班级	1班	2班	3班	4班
实际购数量（本）	_____	33	_____	21
实际购数量与计划购数量的差值（本）	+12	_____	﹣8	﹣9

(1)、完成表格；

(2)、根据记录的数据可知4个班实际一共购书本？

(3)、书店给出两种优惠方案，方案甲：一次购买不少于15本，其中2本书免费；乙方案：如果一次性购书不少于20本，总价9折优惠，假设每本书售价为30元，请你计算初2021届4个班实际购书最少花费多少元？

查看试题解析

26. 点A、B在数轴上分别表示数a、b，A、B之间的距离可表示为 $A B = | a - b |$ ，已知数轴上A，B两点分别表示有理数-1和x.

(1)、若AB=4时，则x的值为；

(2)、当x=7时，点A，B分别以每秒1个单位长度和2个单位长度的速度同时向数轴负方向运动.求经过多少秒后，点A到原点的距离是点B到原点的距离的2倍；

(3)、如图，点A，B，C，D四点在数轴上分别表示的数为-1，0，2，6，是否存在点P在数轴上，使得点P到这四点的距离总和的最小？若存在，请直接写点P的位置和距离总和的最小值.若不存在，请说明理由；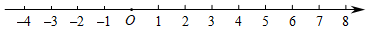

(4)、某一直线沿街有101户民，依次记为 $A_{1} ， A_{2} ， A_{3} ， \dots ， A_{101}$ ，假定相邻两户居民间隔相同，将这个间隔记为1；某餐饮公司想为这101户居民提供早餐，决定在路旁建立一个快餐店P.请问点P选在何处，才能使这101户居民到点P的距离总和最小？最小距离和是多少？

查看试题解析
27. 观察下列等式：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，

将以上三个等式两边分别相加得：

$\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} = 1 - \frac{1}{4} = \frac{3}{4}$ .

(1)、猜想并写出： $\frac{1}{n (n + 1)} =$ .

(2)、直接写出下列各式的计算结果：
① $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2015 \times 2016} =$ ；

② $\frac{1}{2 \times 4} + \frac{1}{4 \times 6} + \frac{1}{6 \times 8} + \dots + \frac{1}{2014 \times 2016} =$ .

(3)、探究并解决问题：
如果有理数a，b满足∣ab－2∣＋∣1－b∣＝0，试求：

$\frac{1}{a b} + \frac{1}{(a + 1) (b + 1)} + \frac{1}{(a + 2) (b + 2)} + \dots + \frac{1}{(a + 2015) (b + 2015)}$ 的值.

查看试题解析
28. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础.

(1)、在数轴上标示出－4、－3、－2、4、

(2)、结合数轴与绝对值的知识回答下列问题：
①数轴上表示4和－2的两点之间的距离是，

表示－2和－4两点之间的距离是.

一般地，数轴上表示数m和数n的两点之间的距离等于|m-n|.

如果表示数a和-2的两点之间的距离是3，即 $| a - (- 2) | = 3$ 那么a=；

②若数轴上表示数a的点位于－3和2之间，则 $| a + 3 | + | a-2 |$ 的值是；

③当a取时，|a+4|+|a-1|+|a-4|的值最小，最小值是

查看试题解析
29. 观察下面的等式：
$\frac{5}{2} - 1 = - | - \frac{1}{2} + 2 | + 3$

$3 - 1 = - | - 1 + 2 | + 3$

$1 - 1 = - | 1 + 2 | + 3$

$(- \frac{1}{2}) - 1 = - | \frac{5}{2} + 2 | + 3$

$(- 2) - 1 = - | 4 + 2 | + 3$

回答下列问题：

(1)、填空： $- 1 = - | 6 + 2 | + 3$ ；

(2)、已知 $2 - 1 = - | x + 2 | + 3$ ，则 $x$ 的值是；

(3)、设满足上面特征的等式最左边的数为 $y$ ，则 $y$ 的最大值是，此时的等式为 .

查看试题解析