初中数学浙教版八年级上学期期末培优专题9 一次函数
试卷更新日期:2020-11-26 类型:复习试卷
一、单选题
-
1. 一次函数y=2x+1的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限2. 如图,已知函数y=kx(k≠0)和y=ax+b(a≠0)的图象交于点P(-3,1),则关于x的不等式kx≥ax+b的解集是( )
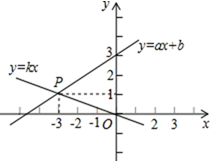 A、 B、 C、 D、3. 看一次函数y=(3-k)x-k的图象经过第一、三、四象限,则k的取值范围是( )A、k>3 B、0<k<3 C、k<0 D、k<34. 已知 是直线 (a为常数)上的两点,若 ,则 的值可以是( )A、 B、0 C、1 D、25. 将直线 向上平移两个单位,平移后的直线所对应的函数关系式为( )A、 B、 C、 D、6. 在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为( )A、2 B、3 C、4 D、67. 2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平,自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示2020年初至脱销期间,该厂库存量y(吨)与时间(天)之间函数关系的大致图象是( )A、
A、 B、 C、 D、3. 看一次函数y=(3-k)x-k的图象经过第一、三、四象限,则k的取值范围是( )A、k>3 B、0<k<3 C、k<0 D、k<34. 已知 是直线 (a为常数)上的两点,若 ,则 的值可以是( )A、 B、0 C、1 D、25. 将直线 向上平移两个单位,平移后的直线所对应的函数关系式为( )A、 B、 C、 D、6. 在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为( )A、2 B、3 C、4 D、67. 2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平,自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示2020年初至脱销期间,该厂库存量y(吨)与时间(天)之间函数关系的大致图象是( )A、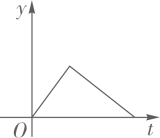 B、
B、 C、
C、 D、
D、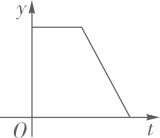 8. 已知在平面直角坐标系xOy中,直线y=2x+2和直线 分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )A、 B、 C、 D、9. 已知一次函数 的图象如图所示,则 的图象可能是( )
8. 已知在平面直角坐标系xOy中,直线y=2x+2和直线 分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )A、 B、 C、 D、9. 已知一次函数 的图象如图所示,则 的图象可能是( )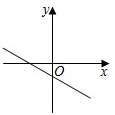 A、
A、 B、
B、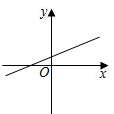 C、
C、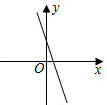 D、
D、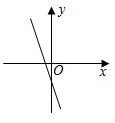 10. 已知一次函数的图象过A(0,1),B(2,0)两点,则下列各点在直线AB上的是( )A、(1,1) B、(4,-1) C、(-1,2) D、(4,-2)
10. 已知一次函数的图象过A(0,1),B(2,0)两点,则下列各点在直线AB上的是( )A、(1,1) B、(4,-1) C、(-1,2) D、(4,-2)二、填空题
-
11. 将长为30cm,宽为10cm的长方形白纸,按如图所示的方发粘合起来,粘合部分的宽为3cm.设x张白纸粘合后的总长度为ycm,则y与x的函数关系式.
 12. y=(m-3)x+m2-9 是正比例函数,则m=13. 已知点 , ,且直线AB与坐标轴围成的三角形面积等于14,则m的值是.14. 已知一次函数y=-2x+b,当-1<x<2时,1<y<7,则b的值为.15. 如图,直线 与 轴、 轴分别交于 ,将△ 沿过点 的直线折叠,使点 落 轴正半轴的 点,折在痕与 轴交于点 ,则折痕所在直线的解析式为.
12. y=(m-3)x+m2-9 是正比例函数,则m=13. 已知点 , ,且直线AB与坐标轴围成的三角形面积等于14,则m的值是.14. 已知一次函数y=-2x+b,当-1<x<2时,1<y<7,则b的值为.15. 如图,直线 与 轴、 轴分别交于 ,将△ 沿过点 的直线折叠,使点 落 轴正半轴的 点,折在痕与 轴交于点 ,则折痕所在直线的解析式为.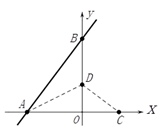 16. 若直线y=kx+b(k≠0)的图象经过点(0,2),且与坐标轴所围成的三角形面积是2,则k的值为17. 如图所示,直线y=kx+b经过点(﹣2,0),则关于x的不等式kx+b<0的解集为 .
16. 若直线y=kx+b(k≠0)的图象经过点(0,2),且与坐标轴所围成的三角形面积是2,则k的值为17. 如图所示,直线y=kx+b经过点(﹣2,0),则关于x的不等式kx+b<0的解集为 .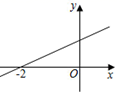 18. 已知:一次函数y=(2﹣m)x+m﹣3.(1)、如果此函数图象经过原点,那么m应满足的条件为;(2)、如果此函数图象经过第二、三、四象限,那么m应满足的条件为;(3)、如果此函数图象与y轴交点在x轴下方,那么m应满足的条件为;(4)、如果此函数图象与y轴交点到x轴的距离为2,那么m应满足的条件为 .19. 直线y=3x向下平移3个单位长度得到的直线是20. 如图,在平面直角坐标系中,一次函数y=- x+4的图象l1与正比例函数y= x的图象l2交于点C.若一次函数y=kx-1的图象为l3,且l1 , l2 , l3不能围成三角形,则满足条件的 k 的值为
18. 已知:一次函数y=(2﹣m)x+m﹣3.(1)、如果此函数图象经过原点,那么m应满足的条件为;(2)、如果此函数图象经过第二、三、四象限,那么m应满足的条件为;(3)、如果此函数图象与y轴交点在x轴下方,那么m应满足的条件为;(4)、如果此函数图象与y轴交点到x轴的距离为2,那么m应满足的条件为 .19. 直线y=3x向下平移3个单位长度得到的直线是20. 如图,在平面直角坐标系中,一次函数y=- x+4的图象l1与正比例函数y= x的图象l2交于点C.若一次函数y=kx-1的图象为l3,且l1 , l2 , l3不能围成三角形,则满足条件的 k 的值为
三、计算题
-
21. 已知一次函数y=kx+b的图像经过点(-2,-4),且与正比例函数 的图像相交于点(4,a ),求:(1)、a的值;(2)、k、b的值22. 如图,直线L:y=- x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
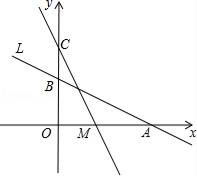 (1)、求A、B两点的坐标;(2)、求△COM的面积S与M的移动时间t之间的函数关系式;(3)、当t为何值时△COM≌△AOB,并求此时M点的坐标.
(1)、求A、B两点的坐标;(2)、求△COM的面积S与M的移动时间t之间的函数关系式;(3)、当t为何值时△COM≌△AOB,并求此时M点的坐标.四、解答题
-
23. 如图,直线 的解析式为: ,且 与x轴交于点D,直线 经过点A,B,直线 , 交于点C.
 (1)、求直线 的解析表达式;(2)、求 的面积.
(1)、求直线 的解析表达式;(2)、求 的面积.五、综合题
-
24. 如图,直线 与x轴、y轴分别交于A、B两点,点C的的坐标为(-6,0),点P(x,y)是直线 上的一个动点(点P不与点A重合).
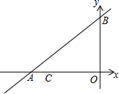 (1)、在点P的运动过程 ,试写出△OPC的面积S与x之间的函数关系式(2)、当点P运动到什么位置时,△OPC的面积为15?求出此时点P的坐标25. 根据市卫生防疫部门的要求,游泳池必须定期换水后才能对外开放.在换水时需要经“排水﹣清冼﹣注水”的过程.某游泳馆从早上8:00开始对游泳池进行换水,已知该游泳池的排水速度是注水速度的2倍,其中游泳池内剩余的水量y(m3)与换水时间x(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)、在点P的运动过程 ,试写出△OPC的面积S与x之间的函数关系式(2)、当点P运动到什么位置时,△OPC的面积为15?求出此时点P的坐标25. 根据市卫生防疫部门的要求,游泳池必须定期换水后才能对外开放.在换水时需要经“排水﹣清冼﹣注水”的过程.某游泳馆从早上8:00开始对游泳池进行换水,已知该游泳池的排水速度是注水速度的2倍,其中游泳池内剩余的水量y(m3)与换水时间x(h)之间的函数图象如图所示,根据图象解答下列问题: (1)、该游泳池清洗需要小时.(2)、求排水过程中的y与x之间的函数关系式,并写出自变量x的取值范围.(3)、求该游泳馆在几点钟换水结束.26. 如图,一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)、该游泳池清洗需要小时.(2)、求排水过程中的y与x之间的函数关系式,并写出自变量x的取值范围.(3)、求该游泳馆在几点钟换水结束.26. 如图,一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.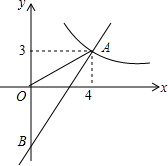 (1)、求函数y=kx+b和y= 的表达式;(2)、已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.27. A,B两城市之间有一条公路相连,公路中途穿过C市,甲车从A市到B市,乙车从C市到A市,甲车的速度比乙车的速度慢20千米/时,两车距离C市的路程y(单位:千米)与驶的时间t(单位:小时)的函数图象如图所示,结合图象信息,解答下列问题:
(1)、求函数y=kx+b和y= 的表达式;(2)、已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.27. A,B两城市之间有一条公路相连,公路中途穿过C市,甲车从A市到B市,乙车从C市到A市,甲车的速度比乙车的速度慢20千米/时,两车距离C市的路程y(单位:千米)与驶的时间t(单位:小时)的函数图象如图所示,结合图象信息,解答下列问题: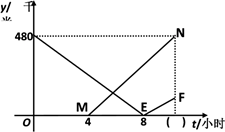 (1)、甲车的速度是千米/时,在图中括号内填入正确的数;(2)、求图象中线段MN所在直线的函数解析式,不需要写出自变量的取值范围;(3)、直接写出甲车出发后几小时,两车距C市的路程之和是460千米.28. 在一条公路上依次有A,B,C三地,甲车从A地出发,驶向C地,同时乙车从C地出发驶向B地,到达B地停留0.5小时后,按原路原速返回C地,两车匀速行驶,甲车比乙车晚1.5小时到达C地.两车距各自出发地的路程y(千米)与时间x(小时)之间的函数关系如图所示.请结合图象信息解答下列问题:
(1)、甲车的速度是千米/时,在图中括号内填入正确的数;(2)、求图象中线段MN所在直线的函数解析式,不需要写出自变量的取值范围;(3)、直接写出甲车出发后几小时,两车距C市的路程之和是460千米.28. 在一条公路上依次有A,B,C三地,甲车从A地出发,驶向C地,同时乙车从C地出发驶向B地,到达B地停留0.5小时后,按原路原速返回C地,两车匀速行驶,甲车比乙车晚1.5小时到达C地.两车距各自出发地的路程y(千米)与时间x(小时)之间的函数关系如图所示.请结合图象信息解答下列问题: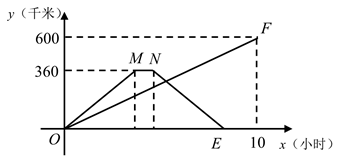 (1)、甲车行驶速度是千米1时,B,C两地的路程为千米;(2)、求乙车从B地返回C地的过程中,y(千米)与x(小时)之间的函数关系式(不需要写出自变量x的取值范围);(3)、出发多少小时,行驶中的两车之间的路程是15千米?请你直接写出答案.29. 我们定义:直线l1:y=mx+n与直线l2:y=nx+m这样的两条直线称为一对交换直线,例如直线y=3x+4与y=4x+3就是一对交换直线,
(1)、甲车行驶速度是千米1时,B,C两地的路程为千米;(2)、求乙车从B地返回C地的过程中,y(千米)与x(小时)之间的函数关系式(不需要写出自变量x的取值范围);(3)、出发多少小时,行驶中的两车之间的路程是15千米?请你直接写出答案.29. 我们定义:直线l1:y=mx+n与直线l2:y=nx+m这样的两条直线称为一对交换直线,例如直线y=3x+4与y=4x+3就是一对交换直线,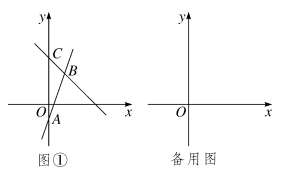 (1)、直线y=-2x+3的交换直线为.(2)、如图①若直线l1:y=3x-1与y轴相交于点A,点B(1,a)在直线l1上.直线l2经过点B,与y轴相交于点C(点C在y轴的正半轴上),且△ABC的面积为2,求证:直线l1与直线l2为一对交换直线;(3)、已知直线l1:y=kx+b(k≠b)和直线l2:y=bx+k相交于点p,且它们是一対交换直线,交点P的纵坐标为4.求p点坐标;30. 如图,四边形 是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正平轴上, .在 边上取一点D,将纸片沿 翻折,使点O落在 边上的点 处.
(1)、直线y=-2x+3的交换直线为.(2)、如图①若直线l1:y=3x-1与y轴相交于点A,点B(1,a)在直线l1上.直线l2经过点B,与y轴相交于点C(点C在y轴的正半轴上),且△ABC的面积为2,求证:直线l1与直线l2为一对交换直线;(3)、已知直线l1:y=kx+b(k≠b)和直线l2:y=bx+k相交于点p,且它们是一対交换直线,交点P的纵坐标为4.求p点坐标;30. 如图,四边形 是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正平轴上, .在 边上取一点D,将纸片沿 翻折,使点O落在 边上的点 处. (1)、求 和 的长;(2)、求直线 的表达式;(3)、直线 与 所在的直线垂直,当它与矩形 有公共点时,求出b的取值范围.
(1)、求 和 的长;(2)、求直线 的表达式;(3)、直线 与 所在的直线垂直,当它与矩形 有公共点时,求出b的取值范围.
-