初中数学浙教版八年级上学期期末培优专题7 坐标平面内图形的轴对称和平移

试卷更新日期：2020-11-26 类型：复习试卷

进入出卷网下载

一、单选题

1. 已知点A（m﹣1，3）与点B（2，n+1）关于x轴对称，则m+n的值为（）

A、1 B、7 C、-1 D、-7

查看试题解析
2. 在平面直角坐标系中，将点 $P (- 3 ， 2)$ 向右平移3个单位得到点 $P^{'}$ ，则点 $P^{'}$ 关于x轴的对称点的坐标为（）

A、 $(0 ， - 2)$ B、 $(0 ， 2)$ C、 $(- 6 ， 2)$ D、 $(- 6 ， - 2)$

查看试题解析
3. 在平面直角坐标系中，线段AB两端点的坐标分别为A(1，0)，B(3，2).将线段AB平移后，A、B的对应点的坐标可以是（）

A、(1，−1)，(−1，−3) B、(1，1)，(3，3) C、(−1，3)，(3，1) D、(3，2)，(1，4)

查看试题解析
4. 如图，把△ABC先向右平移3个单位，再向上平移2个单位得到△DEF，则顶点C（0，-1）对应点的坐标为（）

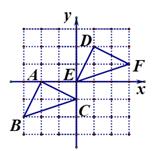A、（0，0） B、（1，2） C、（1，3） D、（3，1）

查看试题解析
5. 已知 $A (3, - 2)$ ， $B (1, 0)$ ，把线段 $A B$ 平移至线段 $C D$ ，其中点A、B分别对应点C、D，若 $C (5, x)$ ， $D (y, 0)$ ，则 $x + y$ 的值是（）

A、-1 B、0 C、1 D、2

查看试题解析
6. 如图，点 $A ， B$ 的坐标分别为 $(1 ， 2)$ ， $(4 ， 0)$ ，将 $Δ A O B$ 沿 $x$ 轴向右平移，得到 $Δ C D E$ ，已知 $D B = 1$ ，则点 $C$ 的坐标为（）

A、 $(2 ， 2)$ B、 $(4 ， 3)$ C、 $(3 ， 2)$ D、 $(4 ， 2)$

查看试题解析
7. 在平面直角坐标系中，一只蚂蚁由(0，0)先向上爬4个单位长度，再向右爬3个单位长度，再向下爬2个单位长度后，它所在位置的坐标是(　　)

A、(4，3) B、(4，2) C、(2，3) D、(3，2)

查看试题解析
8. $Δ D E F$ 是由 $Δ A B C$ 平移得到的，点 $A (- 1 ， - 4)$ 的对应点为 $D (1 ， - 1)$ ，点 $B (1 ， 1)$ 的对应点E、点 $C (- 1 ， 4)$ 的对应点F．则E、F的坐标分别为（）

A、 $(2 ， 2) \begin{matrix} ， & (3 ， 4) \end{matrix}$ B、 $(3 ， 4) \begin{matrix} ， & (1 ， 7) \end{matrix}$ C、 $(- 2 ， 2) \begin{matrix} ， & (1 ， 7) \end{matrix}$ D、 $(3 ， 4) \begin{matrix} ， & (2 ， - 2) \end{matrix}$

查看试题解析
9. 将点 $P (m + 2, 2 m + 1)$ 向左平移1个单位长度到 $P'$ ，且 $P'$ 在y轴上，那么 $P'$ 的坐标是（）

A、 $(0, - 1)$ B、 $(0, - 2)$ C、 $(0, - 3)$ D、 $(1, 1)$

查看试题解析
10. 在平面直角坐标系中，点 A'（2，﹣2）可以由点 A（﹣2，3）通过两次平移得到，则正确的是（）

A、先向左平移4个单位长度，再向上平移5个单位长度； B、先向右平移4个单位长度，再向上平移5个单位长度； C、先向左平移4个单位长度，再向下平移 5 个单位长度； D、先向右平移4个单位长度，再向下平移 5 个单位长度．

查看试题解析
11. 在平面直角坐标系中，已知三角形 ABC 三个顶点坐标分别为 A ( -2，1)、B ( 2，3)、C (-3，-1)，把三角形 ABC 平移到一个确定位置得三角形A ' B ' C '，则对应点A '、B '、C '的坐标可能为（）

A、A'(0，3)， B'(0，1) ，C ' (-1，-1) B、A'(-3，-2) ，B'(3，2) ，C'(-4，0) C、A'(1，-2)，B '(3，2)，C'(-1，-3) D、A'(-1，3) ，B'(3，5) ，C'(-2，1)

查看试题解析
12. 如图，等边△ABC的顶点A(1，1)，B(3，1)，规定把△ABC“先沿x轴翻折，再向左平移1个单位”为一次变换，这样连续经过2020次变换后，等边△ABC的顶点C的坐标为（）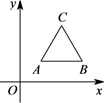

A、(－2 020， $\sqrt{3} + 1$ ) B、(－2 019， $- \sqrt{3} - 1$ ) C、(－2 018， $\sqrt{3} + 1$ ) D、(－2 017， $- \sqrt{3} - 1$ )

查看试题解析
13. 如图，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（0，1），将线段AB平移，使其一个端点到C（3，2），则平移后另一端点的坐标为（）

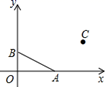A、（1，3） B、（5，1） C、（1，3）或（3，5） D、（1，3）或（5，1）

查看试题解析
14. 在平面直角坐标系中，点P与点M关于y轴对称，点N与点M关于x轴对称，若点P的坐标为(－2,3)，则点N的坐标为（）

A、(－3,2) B、(2,3) C、(2,－3) D、(－2,－3)

查看试题解析
15. 如图，在平面直角坐标系xOy中，点P(1，0).点P第1次向上跳动1个单位至点P₁(1，1)，紧接着第2次向左跳动2个单位至点P₂(﹣1，1)，第3次向上跳动1个单位至点P₃ ，第4次向右跳动3个单位至点P₄ ，第5次又向上跳动1个单位至点P₅ ，第6次向左跳动4个单位至点P₆ ， ….照此规律，点P第100次跳动至点P₁₀₀的坐标是（）

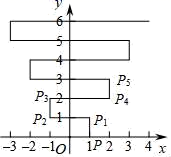A、(﹣26，50) B、(﹣25，50) C、(26，50) D、(25，50)

查看试题解析

二、填空题

16. 已知点P（3，﹣1）关于y轴对称的点Q的坐标是（a，b），则a+b的值.

查看试题解析
17. 如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为： $A (- 2 ， 0)$ ， $B (1 ， 2)$ ， $C (1 ， - 2)$ .已知 $N (- 1 ， 0)$ ，作点N关于点 $A$ 的对称点 $N_{1}$ ，点 $N_{1}$ 关于点 $B$ 的对称点 $N_{2}$ ，点 $N_{2}$ 关于点 $C$ 的对称点 $N_{3}$ ，点 $N_{3}$ 关于点 $A$ 的对称点 $N_{4}$ ，点 $N_{4}$ 关于点 $B$ 的对称点 $N_{5}$ ，…，依此类推，则点 $N_{2020}$ 的坐标为.

查看试题解析
18. 点 $N (- 3, - 2)$ 向平移2个单位后，所对应的点的坐标是 $(- 5, - 2)$ .

查看试题解析
19. 在平面直角坐标系中，已知点A的坐标为（3，2）．设点A关于y轴的对称点为B ，点A关于原点O的对称点为C ，点A绕点O顺时针旋转90°得点D ．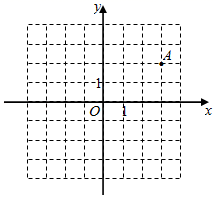

(1)、点B的坐标是；
点C的坐标是；

点D的坐标是；

(2)、顺次联结点A、B、C、D ，那么四边形ABCD的面积是．

查看试题解析
20. 在平面直角坐标系中，已知点 $P (a ， - 1)$ ，请解答下列问题：

(1)、若点 $P$ 在第三象限，则 $a$ 的取值范围为

(2)、若点 $P$ 在 $y$ 轴上，则 $a$ 的值为

(3)、当 $a = 2$ 时，点 $P$ 关于 $y$ 轴对称的点的坐标为点 $P$ 关于原点对称的点的坐标为

查看试题解析
21. $Δ A B C$ 三个顶点坐标 $A (- 4 ， - 3)$ ， $B (0 ， - 3)$ ， $C (- 2 ， 0)$ ，将点 $B$ 向右平移2个长度单位后，再向上平移5个长度单位到 $D$ ，若设 $Δ A B C$ 面积为 $S_{1}$ ， $Δ A D C$ 的面积为 $S_{2}$ ，则 $S_{1}$ 与 $S_{2}$ 大小关系为．

查看试题解析
22. 在平面直角坐标系中，已知点 $A (- 4, 0)$ 和 $B (0, 1)$ ，现将线段 $A B$ 沿着直线 $A B$ 平移，使点A与点B重合，则平移后点 $B$ 坐标是.

查看试题解析
23. 如图，在直角坐标系中，已知A(4，4)，B(-1，1)，EF=1，线段EF在x轴上平移，当四边形ABEF的周长最小时，点E坐标是.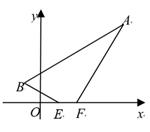

查看试题解析
24. 在平面直角坐标系中，已知A（-1，1），B（1，1），若要在x轴上找一点P，使AP+BP最短，则点P的坐标为.

查看试题解析
25. 已知点P₁与P₂ ， P₂与P₃分别关于y轴和x轴对称，若点P₁在第一象限，则点P₃在第象限．

查看试题解析

三、解答题

26. 已知在平面直角坐标系中，线段AB的两个端点坐标分别为A（2，5），B（6，−2），点P（m，n）为线段AB上一点，若平移AB使其两个端点都落在坐标轴上，求平移后点P的坐标

查看试题解析
27. 如图，在平面直角坐标系中有一个△ABC，顶点A（-1，3），B（2，0），C（-3，-1）．

(1)、画出△ABC关于y轴的对称图形△A₁B₁C₁（不写画法）；
点A关于x轴对称的点坐标为

点B关于y轴对称的点坐标为

点C关于原点对称的点坐标为

(2)、若网格上的每个小正方形的边长为1，则△ABC的面积是．

查看试题解析

四、综合题

28. 如图，在直角坐标平面内，点A的坐标是（0，3），点B的坐标是（﹣3，﹣2）．

(1)、图中点C关于x轴对称的点D的坐标是．

(2)、如果将点B沿着与y轴平行的方向向上平移5个单位得到点B₁ ，那么A、B₁两点之间的距离是．

(3)、求三角形ACD的面积．

查看试题解析
29. 如图，在直角坐标平面内，点A的坐标是 $(0 ， 3)$ ，点B的坐标是 $(- 3 ， - 2)$

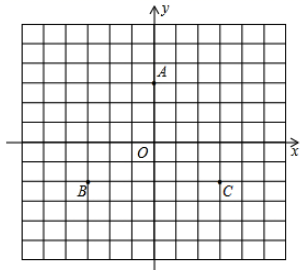(1)、图中点C关于x轴对称的点D的坐标是．

(2)、如果将点B沿着与x轴平行的方向向右平移3个单位得到点 $B^{'}$ ，那么 $A$ 、 $B^{'}$ 两点之间的距离是．

(3)、求四边形ABCD的面积

查看试题解析
30. △ABC与△A₁B₁C₁在平面直角坐标系中的位置如图所示

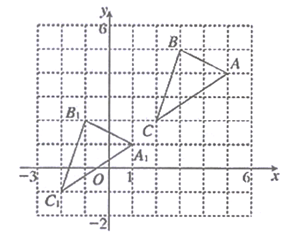(1)、分别写出下列各点的坐标：A；C；C₁；

(2)、△A₁B₁C₁由△ABC经过怎样的平移得到?

(3)、若点P(a+4，a+4)是△ABC内部一点，则△A₁B₁C₁内部的对应点P₁恰好在x轴上，那么P₁坐标为；

(4)、求△ABC面积。

查看试题解析
31. 如图，点 $A ， B$ 的坐标分别为 $(2 ， 0) ， (0 ， 1)$ ，将线段 $A B$ 直接平移到 $M N$ ，使点A移至点M的位置，点B移至点N的位置，设平移过程中线段 $A B$ 扫过的面积为S，

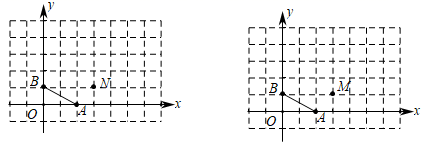(1)、如图1，若点N的坐标是 $(3 ， 1)$ ，则点M的坐标为，请画出平移后的线段 $M N$ ；

(2)、如图2，若点M的坐标是 $(3 ， 1)$ ，请画出平移后的线段 $M N$ ，则S的值为；

(3)、若 $S = 2.5$ ，且点M在坐标轴上，请直接写出所有满足条件的M点的坐标.

查看试题解析
32. 平面直角坐标系xOy中，有点P（a，b），实数a，b，m满足以下两个等式：
2a﹣3m+1=0，3b﹣2m﹣16=0

(1)、当a=1时，点P到x轴的距离为；

(2)、若点P落在x轴上，点P平移后对应点为P′（a+15，b+4），求点P和P′的坐标；

(3)、当a≤4＜b时，求m的最小整数值.

查看试题解析
33. 已知点 $A (a ， 0)$ 和 $B (0 ， b)$ 满足 ${(a - 4)}^{2} + | b - 6 | = 0$ ，分别过点A、B作x轴、y轴的垂线交于点C，如图，点P从原点出发，以每秒2个单位长度的速度沿着 $O - B - C - A - O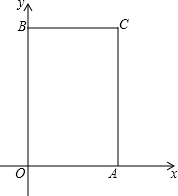$ 的路线移动.

(1)、写出A、B、C三点的坐标；

(2)、当点P移动了6秒时，描出此时P点的位置，并写出点P的位置；

(3)、连结 $(2)$ 中B、P两点，将线段BP向下平移h个单位 $(h > 0)$ ，得到 $B' P'$ ，若 $B' P'$ 将四边形OACB的周长分成相等的两部分，求h的值.

查看试题解析
34. 如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为（4，0），C点的坐标为（0，3），点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动（即：沿着长方形移动一周）．

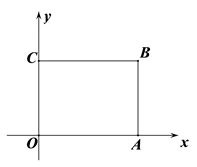(1)、直接写出B点的坐标；

(2)、当点P移动了3秒时，请直接写出点P的坐标；

(3)、在移动过程中，当点P到x轴距离为2个单位长度时，求点P移动的时间．

查看试题解析
35. 如图是由边长为1的小正方形组成的网格图．

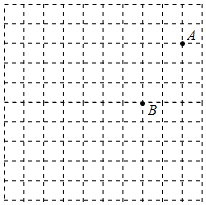(1)、请在网格图中建立平面直角坐标系xOy ，使点A的坐标为 $(3 ， 3)$ ，点B的坐标为 $(1 ， 0)$ ；

(2)、若点C的坐标为 $(4 ， 1)$ ， $△ A B C$ 关于y轴对称三角形为 $△ A_{1} B_{1} C_{1}$ ，则点C的对应点 $C_{1}$ 坐标为；

(3)、已知点D为y轴上的动点，求 $△ A B D$ 周长的最小值．

查看试题解析