初中数学浙教版八年级上学期期末培优专题6 平面直角坐标系

试卷更新日期：2020-11-26 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图是人民公园的部分平面示意图，为准确表示地理位置，可以建立坐标系用坐标表示地理位置，若牡丹园的坐标是 $(2 ， 2)$ ，南门的坐标是 $(0 ， - 3)$ ，则湖心亭的坐标为（）

A、 $(- 1 ， 3)$ B、 $(- 3 ， 1)$ C、 $(- 3 ， - 1)$ D、 $(3 ， - 1)$

查看试题解析
2. 为了全面保障学校艺术节表演的整体效果，王老师在操场中标记了几个关键位置，如图是利用平面直角坐标系画出的关键位置分布图，若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示点A的坐标为(-1，-2)，表示点B的坐标为（1，1），则表示其他位置的点的坐标正确的是（）

A、C(-1，0) B、D(-3，1) C、E(-7，-3) D、F(2，-3)

查看试题解析
3. 如图为小平与小聪微信对话记录，根据两人的对话记录，若下列有一种走法能从科技馆出发走到小平家，则可行的是（）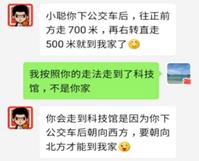

A、向北直走200米，再向东直走1200米 B、向北直走200米，再向西直走1200米 C、向北直走500米，再向东直走700米 D、向北直走700米，再向西直走500米

查看试题解析
4. 小丽在某动物园的大门口看到这个动物园的平面示意图(如图).若她以大门为坐标原点，向右与向上分别为x轴、y轴的正方向建立平面直角坐标系，则其他四个景点大致用坐标表示肯定错误的是（）

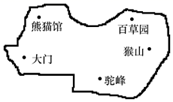A、熊猫馆(1，4) B、猴山(6，1) C、百草园(5，-3) D、驼峰(5，-2)

查看试题解析
5. 如图，棋盘上若“将”位于（2，﹣2），“象”位于（4，﹣2），则“炮”位于（）

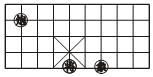A、（﹣2，1） B、（﹣1，2） C、（﹣1，1） D、（﹣2，2）

查看试题解析
6. 如图，在一次“寻宝”游戏中，寻宝人找到了如图所示的两个标志点A（3，1），B（2，2），则“宝藏”点C的位置是（）

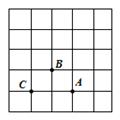A、（1，0） B、（1，2） C、（2，1） D、（1，1）

查看试题解析
7. 如果点P(m， $1 - m$ )在第四象限，则m的取值范围是（）

A、 $m > 0$ B、 $0 < m < 1$ C、 $m < 1$ D、 $m > 1$

查看试题解析
8. 已知点 $P (x - 1, x - 3)$ 在第一象限或第三象限，则 $x$ 的取值范围是（）

A、 $x = 3$ B、 $x < 1$ C、 $1 < x < 3$ D、 $x < 1$ 或 $x > 3$

查看试题解析
9. 如图，在平面直角坐标系.点 A₁、A₂、A₃、A₄、A₅、A₆ 的坐标依次为 A₁(0，1)， A₂(1，1)，A₃(1，0)，A₄(2，0)，A₅(2，1)，A₆(3，1)，…按此规律排列，则点 A₂₀₂₀的坐标是（）

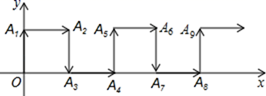A、(1009，1) B、(1009，0) C、(1010，1) D、(1010，0)

查看试题解析
10. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点 $(1 ， 1)$ ，第2次运动到点 $(2 ， 0)$ ，第3次运动到点 $(3 ， - 1)$ ，···，按照这样的运动规律，点P第17次运动到点（）

A、 $(17 ， 1)$ B、 $(17 ， 0)$ C、 $(17 ， - 1)$ D、 $(18 ， 0)$

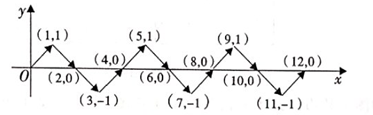查看试题解析
11. 已知点A(2x﹣4，x+2)在坐标轴上，则x的值等于（）

A、2或﹣2 B、﹣2 C、2 D、非上述答案

查看试题解析
12. 点P的横坐标是-3，且到x轴的距离为5，则P点的坐标是（）

A、 $(5, - 3)$ 或 $(- 5, - 3)$ B、 $(- 3, 5)$ 或 $(- 3, - 5)$ C、 $(- 3, 5)$ D、 $(- 3, - 5)$

查看试题解析
13. 已知点 $P (x, y)$ 为第四象限内一点，且满足 $| x | = 3$ ， $y^{2} = 4$ ，则P点的坐标为（）

A、 $(- 3 ， 2)$ B、 $(3,2)$ C、 $(3 ， - 2)$ D、 $(- 3 ， - 2)$

查看试题解析
14. 如图，在 $4 \times 8$ 的长方形网格 $O A B C$ 中，动点 $P (0 ， 3)$ 从出发，沿箭头所示方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，当点 $P$ 第2020次碰到矩形的边时，点 $P$ 的坐标为（）

A、 $(1 ， 4)$ B、 $(5 ， 0)$ C、 $(6 ， 4)$ D、 $(8 ， 3)$

查看试题解析
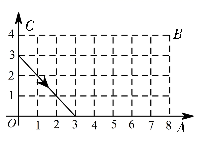15. 在平面直角坐标系xOy中，对于点P(x，y)，我们把点P′(-y+1，x+1)叫做点P伴随点.已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得到点A₁ ， A₂ ， A₃ ， …，A_n ， ….若点A₁的坐标为(2，4)，点A₂₀₂₀的坐标为（）

A、(-3，3) B、(-2，-2) C、(3，-1) D、(2，4)

查看试题解析

二、填空题

16. 如图，在x轴，y轴上分别截取OA，OB，使OA=OB，再分别以点A，B为圆心，以大于 $\frac{1}{2}$ AB长为半径画弧，两弧交于点P.若点P的坐标为（a，2a-3），则a的值为.

查看试题解析
17. 在平面直角坐标系中，如果一个点的横、纵坐标均为整数，那么我们称该点为整点，若整点P（m+2， $\frac{1}{2}$ m﹣1）在第四象限，则m的值为.

查看试题解析
18. 在平面直角坐标系中，点A1(1，1)，A2(2，4)，A3(3，9)，A4(4，16)，…，用你发现的规律确定点A9的坐标为．

查看试题解析
19. 如图，A、B两点的坐标分别为（﹣2，1）、（4，1），在同一坐标系内点C的坐标为．

查看试题解析
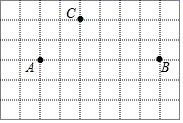20. 如图，长方形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A(2，0)同时出发，沿长方形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2018次相遇地点的坐标是．

查看试题解析
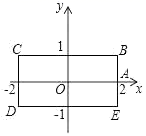21. 平面直角坐标系中，已知点A（2，0），B（0，3），点P（m，n）为第三象限内一点，若DPAB的面积为18，则m，n满足的数量关系式为.

查看试题解析
22. 如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动一个单位，依次得到点P₁（0，1）；P₂（1，1）；P₃（1，0）；P₄（1，﹣1）；P₅（2，﹣1）；P₆（2，0）……，则点P₂₀₁₉的坐标是．

查看试题解析
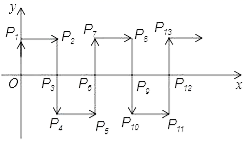23. 如图，已知A（3，0），B（0，﹣1），连接AB，过点B的垂线BC，使BC＝BA，则点C坐标是．

查看试题解析
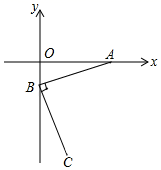24. 在平面直角坐标系中，若点 $A (0 ， 4)$ ， $B (3 ， 0)$ ，则 $A B = 5$ .请在 $x$ 轴上找一点 $C$ ，使 $Δ A B C$ 是以 $A B$ 为腰的等腰三角形，点 $C$ 的坐标为.

查看试题解析
25. 如图，直线BC经过原点O，点A在x轴上，AD⊥BC于D，若点B(m，3)，C(n，-5)，A(4，0)，则AD·BC=。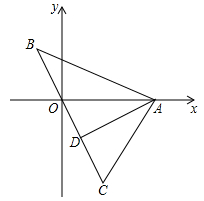

查看试题解析

三、作图题

26. 如图，四边形 $A B C D$ 所在的网格图中，每个小正方形的边长均为1个单位长度.

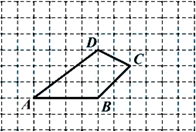(1)、建立以点 $B$ 为原点， $A B$ 边所在直线为 $x$ 轴的直角坐标系；

(2)、写出点 $A$ 、 $B$ 、 $C$ 、 $D$ 的坐标；

(3)、求出四边形 $A B C D$ 的面积.

查看试题解析
27. 如图，四边形ABCD所在的网格图中，每个小正方形的边长均为1个单位长度.

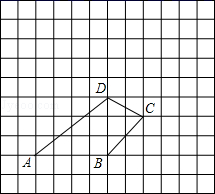(1)、建立以点B为原点，AB边所在直线为x轴的直角坐标系.写出点A、B、C、D的坐标；

(2)、求出四边形ABCD的面积；

(3)、请画出将四边形ABCD向上平移5格，再向左平移2格后所得的四边形A′B′C′D′.

查看试题解析
28. 如图，在平面直角坐标系中，A（﹣1，﹣2），B（﹣2，﹣4），C（﹣4，﹣1）．

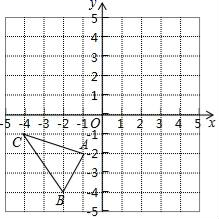(1)、把△ABC向上平移2个单位长度，再向右平移1个单位长度后得到△A₁B₁C₁ ，请画出△A₁B₁C₁ ，并写出点A₁ ， B₁ ， C₁的坐标；

(2)、求△A₁B₁C₁的面积；

(3)、点P在坐标轴上，且△A₁B₁P的面积是2，求点P的坐标．

查看试题解析

四、综合题

29. 已知点P(m＋2，3)，Q(−5，n−1)，根据以下条件确定m、n的值

(1)、P、Q两点在第一、三象限的角平分线上；

(2)、PQ∥x轴，且P点与Q点的距离为3．

查看试题解析
30. 已知：P（4x，x-3）在平面直角坐标系中.

(1)、若点P在第三象限的角平分线上，求x的值；

(2)、若点P在第四象限，且到两坐标轴的距离之和为9，求x的值.

查看试题解析
31. 已知：长方形ABCD在坐标平面内的位置如图所示， A(1，1) C(-3，-4)，点P从点A出发，沿着A→B→C→D→A的路径，以每秒 $\frac{1}{2}$ 个单位的速度运动．运动一周回到A点时停止运动．设运动时间为t秒．

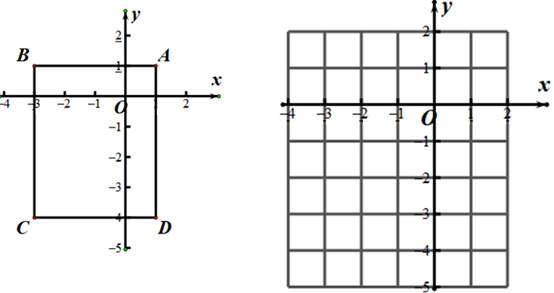(1)、直接写出点B、点D的坐标．

(2)、当t=6秒时，写出P点的坐标．

(3)、当点P运动到与x轴的距离为 $\frac{1}{2}$ 个单位时直接写出t的值．

查看试题解析
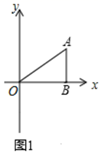
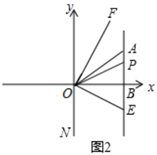32. 已知在平面直角坐标系中，点 $A (a ， b)$ 满足 $\frac{1}{2} \sqrt{a - 3} + {(2 - b)}^{2} = 0$ ， $A B ⊥ x$ 轴于点 $B$ ．

(1)、点 $A$ 的坐标为，点 $B$ 的坐标为；

(2)、如图1，若点 $M$ 在 $x$ 轴上，连接 $M A$ ，使 $S_{△ A B M} = 2$ ，求出点 $M$ 的坐标；

(3)、如图2， $P$ 是线段 $A B$ 所在直线上一动点，连接 $O P$ ， $O E$ 平分 $∠ P O N$ ，交直线 $A B$ 于点 $E$ ，作 $O F ⊥ O E$ ，当点 $P$ 在直线 $A B$ 上运动过程中，请探究 $∠ O P E$ 与 $∠ F O P$ 的数量关系，并证明．

查看试题解析
33. 如图平面直角坐标系中，A点坐标为（0，1），AB＝BC＝ $\sqrt{10}$ ，∠ABC＝90°，CD⊥x轴．

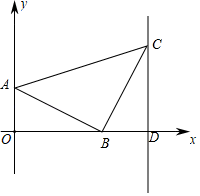(1)、填空：B点坐标为， C点坐标为．

(2)、若点P是直线CD上第一象限上一点且△PAB的面积为6.5，求P点的坐标；

(3)、在（2）的条件下点M是x轴上线段OD之间的一动点，当△PAM为等腰三角形时，直接写出点M的坐标．

查看试题解析