初中数学浙教版八年级上学期期末培优专题5 一元一次不等式组

试卷更新日期：2020-11-26 类型：复习试卷

进入出卷网下载

一、单选题

1. 关于x的不等式组 ${\begin{array}{l} 3 x - 1 > 4 (x - 1) \\ x < a \end{array}$ 的解集为 $x < 3$ ，那么a的取值范围为（）

A、 $a > 3$ B、 $a < 3$ C、 $a \geq 3$ D、 $a \leq 3$

查看试题解析
2. 一次智力测验，有20道选择题，评分标准：答对1题给5分，答错1题扣2分，不答题不给分也不扣分，小明有两道题未答，他最后的总分不低于60分，则小明至少答对的题数是（）

A、14道 B、13道 C、12道 D、11道

查看试题解析
3. 不等式组 ${\begin{matrix} x + 1 > 2 \\ 2 x - 4 \leq x \end{matrix}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
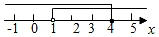4. 不等式组 ${\begin{array}{l} x + 1 \geq 2 x - 1 \\ 4 x + 5 > 2 (x + 1) \end{array}$ 的整数解有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 某单位为响应政府号召，需要购买分类垃圾桶6个，市场上有A型和B型两种分类垃圾桶，A型分类垃圾桶500元/个，B型分类垃圾桶550元/个，总费用不超过3100元，则不同的购买方式有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
6. 若关于x的不等式组 ${\begin{array}{l} 3 x - 5 ⩾ 1 \\ 2 x - a < 8 \end{array}$ 有且只有3个整数解，则a的取值范围是（）

A、 $0 \leq a \leq 2$ B、 $0 \leq a < 2$ C、 $0 < a \leq 2$ D、 $0 < a < 2$

查看试题解析
7. 若关于x的不等式组 ${\begin{array}{l} \frac{2 - x}{2} > \frac{2 x - 4}{3} \\ - 3 x > - 2 x - a \end{array}$ 的解集是 $x < 2$ ，则a的取值范围是（）

A、 $a \geq 2$ B、 $a < - 2$ C、 $a > 2$ D、 $a \leq 2$

查看试题解析
8. 若关于x的不等式组 ${\begin{array}{l} x - m < 0 \\ 3 - 2 x ⩽ 1 \end{array}$ 所有整数解的和是6，则m的取值范围是（）

A、2＜m≤3 B、2≤m＜3 C、3＜m≤4 D、3≤m＜4

查看试题解析
9. 关于 $x$ 的不等式组 ${\begin{array}{l} m - x > 0 \\ 2 x - 7 \geq - 1 \end{array}$ 的整数解共有4个，则 $m$ 的取值范围是（）

A、6≤ $m$ ≤7 B、6＜ $m$ ≤7 C、6≤ $m$ ＜7 D、6＜ $m$ ＜7

查看试题解析
10. 如图，这是王彬同学设计的一个计算机程序，规定从“输入一个值x”到判断“结果是否≥13”为一次运行过程.如果程序运行两次就停止，那么x的取值范围是（）

A、x≥7 B、4≤x＜7 C、4＜x≤7 D、x＜7

查看试题解析
11. 下列说法正确的是（）

A、若 $a < b$ ，则 $a x < b x$ B、 $a$ 为任意实数，则 $a + 2$ 一定大于 $a$ ，同时 $a + 2$ 也一定大于 $2$ C、不等式： $\frac{x - 5}{2} + 1 > x - 3$ 有无数个解 D、不等式组： ${\begin{array}{l} 3 x - 2 < x + 1 \\ x + 5 > 4 x + 1 \end{array}$ 的解集是 $x < \frac{3}{2}$

查看试题解析
12. 如果关于x的不等式组 ${\begin{array}{l} \frac{x}{3} - 1 \leq \frac{1}{2} (x - 1) \\ 2 x - a \leq 3 (1 - x) \end{array}$ 有且只有三个整数解，且关于x的方程2+a=3(4﹣x)有整数解，那么符合条件的所有整数a的和为（）

A、﹣5 B、﹣6 C、﹣9 D、﹣13

查看试题解析
13. 小艾在母亲节给妈妈送了一束鲜花，出差在外的爸爸问小艾送了些什么花．小艾调皮地说：“考考你，花束是由象征爱的康乃馨、玫瑰和百合花组成．康乃馨的支数比玫瑰多，但比百合花的两倍少，玫瑰的支数比百合多．”请帮小艾爸爸算一算，这束花的总支数至少为（）

A、11 B、12 C、13 D、14

查看试题解析
14. 与不等式 $\frac{x - 3}{2}$ ＜ $\frac{2 x + 1}{3}$ -1有相同解集的不等式是（　　）

A、3x-3＜（4x+1）-1 B、3（x-3）＜2（2x+1）-1 C、2（x-3）＜3（2x+1）-6 D、3x-9＜4x-4

查看试题解析
15. 如图，按下面的程序进行运算，规定程序运行到“判断结果是否大于30”为一次运算．若运算进行了3次才停止，则x的取值范围是（）

A、 $\frac{51}{8} \leq x \leq \frac{39}{4}$ B、 $\frac{51}{8} \leq x < \frac{39}{4}$ C、 $\frac{51}{8} < x \leq \frac{39}{4}$ D、 $\frac{51}{8} < x < \frac{39}{4}$

查看试题解析

二、填空题

16. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} x - 1 > 0 \\ 2 x - a > 0 \end{array}$ 的解是 $x > 1$ ，则 $a$ 的取值范围是．

查看试题解析
17. 我市认真落实国家“精准扶贫”政策，计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩，根据市场调查，甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元，每亩的销售额分别为2万元、2.5万元，如果要求种植成本不少于98万元，但不超过100万元，且所有火龙果能全部售出，则该县在此项目中获得的最大利润是万元．（利润＝销售额﹣种植成本）

查看试题解析
18. 关于x的不等式组 ${\begin{array}{l} 2 x < 3 (x - 3) + 1 \\ \frac{3 x + 2}{4} > x + a \end{array}$ 有四个整数解，则a的取值范围是.

查看试题解析
19. 《西游记》、《三国演义》、《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著某兴趣小组阅读四大名著的人数，同时满足以下三个条件：
（ 1 ）阅读过《西游记》的人数多于阅读过《水浒传》的人数；

（ 2 ）阅读过《水浒传》的人数多于阅读过《三国演义》的人数；

（ 3 ）阅读过《三国演义》的人数的2倍多于阅读过《西游记》的人数.

若阅读过《三国演义》的人数为4，则阅读过《水浒传》的人数的最大值为.

查看试题解析
20. 对于任意实数p、q，定义一种运算 $p ※ q = p - q + p q - 2$ ，等式的右边是通常的加减和乘法运算，例如： $4 ※ 5 = 4 - 5 + 4 \times 5 - 2 = 17$ .请根据上述定义解决问题：若关于 $x$ 的不等式组 ${\begin{array}{l} 2 ※ x < 4 ， \\ x ※ 3 \geq 2 m \end{array}$ 有5个整数解，则m的取值范围是.

查看试题解析
21. 关于x的不等式组 ${\begin{matrix} x - b > 2 a ， \\ x - a < 2 b \end{matrix}$ 的解集为-3<x<3，则a，b的值分别为.

查看试题解析
22. 格格和妈妈到福利院看望失去父母的孤儿，她用自己的零花钱买来棒棒糖分给福利院的小朋友。若每人分4块棒棒糖，则剩下26块；若每人分5块棒棒糖，则最后一名小朋友分得的糖数多于2块，但是不够5块。若已知这些小朋友的数量为偶数个，则共有个小朋友，块棒棒糖．

查看试题解析
23. 如图，天平左盘中物体A的质量为x克，天平右盘中每个砝码的质量都是5克那么x的取值范围为．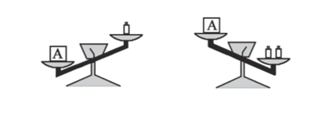

查看试题解析
24. 关于 $x$ 的不等式组 ${\begin{array}{l} 9 x - a > 0, \\ 8 x - b \leq 0 \end{array}$ 的整数解仅有2，3，4，则 $a$ 的取值范围是， $b$ 的取值范围是．

查看试题解析
25. 在“新冠肺炎”这场没有硝烟的战争中，各行各业都涌现出了一批“最美逆行者”，其中抗疫最前沿的就是护士。某医院护安排护士若干名负责护理新冠病人，每名护士护理4名新冠病人，有20名新冠病人没人护理，如果每名护士护理8名新冠病人，有一名护士护理的新冠病人多于1人不足8人，这个医院安排了名护士护理新冠病人。

查看试题解析

三、计算题

26. 解不等式组：

(1)、 $7 x - 2 < 9 x + 3$

(2)、 ${\begin{matrix} 5 x + 3 > 3 (x - 2) \\ \frac{x + 1}{2} \leq \frac{5 - x}{6} + 1 \end{matrix}$

查看试题解析
27. 解不等式组 ${\begin{array}{l} 5 x + 5 \geq 3 (x - 1) \\ \frac{1}{2} x - 1 < 4 - \frac{3}{2} x \end{array}$ (并把解集表示在数轴上，写出所有的整数解).

查看试题解析

四、解答题

28. 某班级为践行“绿水青山就是金山银山”的理念，开展植树活动．如果每人种3棵，则剩86棵；如果每人种5棵，则最后一人有树种但不足3棵．请问该班有多少学生？本次一共种植多少棵树？（请用一元一次不等式组解答）

查看试题解析
29. 阅读理解题
先阅读理解下面的问题，再按要求完成下列问题

例：解不等式 $(x - 2) (x + 1) > 0$

解：由有理数的乘法法则“两数相乘，同号得正”有① ${\begin{array}{l} x - 2 > 0 \\ x + 1 > 0 \end{array}$ 或② ${\begin{array}{l} x - 2 < 0 \\ x + 1 < 0 \end{array}$

解不等式组①，得 $x > 2$

解不等式组②，得 $x < - 1$

所以不等式 $(x - 2) (x + 1) > 0$ 的解集为 $x > 2$ 或 $x < - 1$

解不等式： $\frac{5 x + 1}{2 x - 3} < 0$

查看试题解析
30. 小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表.为了节约资金,小明应选择哪一种购买方案?请说明理由.

大笔记本

小笔记本

价格(元/本)

6

5

页数(页/本)

100

60

查看试题解析

五、综合题

31. 某商场筹集资金12.8万元，一次性购进空调、彩电共30台，根据市场需要，这些空调，彩电可以全部销售，计划全部销售后利润不少于2.25万元，其中空调，彩电的进价和售价见表格：

空调

彩电

进价（元/台）

5000

3200

售价（元/台）

5800

3900

设商场计划购进空调x台

(1)、空调和彩电全部销售后商场获得的利润为y元，求出y与x的函数关系式；

(2)、商场有哪几种进货方案可供选择？

(3)、由于商场的空调进行了促销活动，实际空调获利只有计划的80%，按原计划的哪个进货方案，商场获利最大？最大利润是多少元？

查看试题解析
32. 众志成城抗疫情，全国人民在行动.某公司决定安排大、小货车共20辆，运送260吨物资到A地和B地，支援当地抗击疫情.每辆大货车装15吨物资，每辆小货车装10吨物资，这20辆货车恰好装完这批物资.已知这两种货车的运费如下表：

A地（元/辆）

B地（元/辆）

大货车

900

1000

小货车

500

700

现安排上述装好物资的20辆货车（每辆大货车装15吨物资，每辆小货车装10吨物资）中的10辆前往A地，其余前往B地，设前往A地的大货车有x辆，这20辆货车的总运费为y元.

(1)、这20辆货车中，大货车、小货车各有多少辆？

(2)、求 $y$ 与 $x$ 的函数解析式，并直接写出 $x$ 的取值范围；

(3)、若运往A地的物资不少于140吨，求总运费y的最小值.

查看试题解析
33. 某文具店计划购进 $A 、 B$ 两种计算器共 $60$ 个，若购进 $A$ 种计算器的数量不少于 $B$ 种计算器数量的 $2$ 倍，且不超过 $B$ 种计算器数量的 $3$ 倍，

(1)、求文具店共有几种进货方案？

(2)、若销售每个 $A$ 种计算器可获利润 $20$ 元，销售每个 $B$ 种计算器可获利润 $35$ 元，则哪一种进货方案获得的利润最大？最大利润是多少？

查看试题解析
34. 小丽准备完成题目：解一元一次不等式组 ${\begin{array}{l} x - 2 > 1 \\ x + □ > 0 \end{array}$ 发现常数“□”印刷不清楚，

(1)、他把“□”猜成－5，请你解一元一次不等式组 ${\begin{array}{l} x - 2 > 1 \\ x - 5 > 0 \end{array}$ ；

(2)、张老师说：我做一下变式，若“□”表示字母a，且 ${\begin{array}{l} x - 2 > 1 \\ x + □ > 0 \end{array}$ 的解集是x＞3，请你求出字母“a”的取值范围.

查看试题解析
35. 兴华商店准备购进甲、乙两种书包出售，每个甲种书包的进价比每个乙种书包的进价多20元，购进3个甲种书包的费用和购进4个乙种书包的费用相等，现计划购进两种书包共100个，其中乙种书包不少于35个．

(1)、甲种书包进价为元/个，乙种书包进价为元/个；

(2)、若甲种书包每个售价120元，乙种书包每个售价90元，且购进这100个书包的费用不低于7200元，如果这100个书包都可售完，那么兴华商店如何进货才能获得最大利润？最大利润是多少？

查看试题解析

	大笔记本	小笔记本
价格(元/本)	6	5
页数(页/本)	100	60

	空调	彩电
进价（元/台）	5000	3200
售价（元/台）	5800	3900

	A地（元/辆）	B地（元/辆）
大货车	900	1000
小货车	500	700