初中数学浙教版八年级上学期期末培优专题3 直角三角形
试卷更新日期:2020-11-26 类型:复习试卷
一、单选题
-
1. 如图, 中,∠B=90°,BC=3,AC=4,则AB的长度为( )
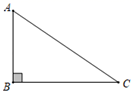 A、2 B、 C、 D、52. 等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形底边上的高为( )A、 B、 C、 D、 或3. 直角三角形两直角边分别为5、12,则这个直角三角形斜边上的高为( )A、6 B、8.5 C、 D、4. 如图,方格中的点A,B,C,D,E称为“格点”(格线的交点),以这5个格点中的3点为顶点画三角形,可以画等腰三角形和直角三角形的个数分别是( )
A、2 B、 C、 D、52. 等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形底边上的高为( )A、 B、 C、 D、 或3. 直角三角形两直角边分别为5、12,则这个直角三角形斜边上的高为( )A、6 B、8.5 C、 D、4. 如图,方格中的点A,B,C,D,E称为“格点”(格线的交点),以这5个格点中的3点为顶点画三角形,可以画等腰三角形和直角三角形的个数分别是( )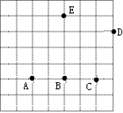 A、2和3 B、3和3 C、2和4 D、3和45. 以下列各组数为边长,能组成直角三角形的是( )A、5,8,10 B、8,15,17 C、4,5,7 D、7,19,216. 如图, ,且 , , ,则线段 的长为( )
A、2和3 B、3和3 C、2和4 D、3和45. 以下列各组数为边长,能组成直角三角形的是( )A、5,8,10 B、8,15,17 C、4,5,7 D、7,19,216. 如图, ,且 , , ,则线段 的长为( )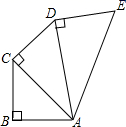 A、1.5 B、2 C、2.5 D、37. 如图,已知 中, 的垂直平分线分别交 于 连接 ,则 的长为( )
A、1.5 B、2 C、2.5 D、37. 如图,已知 中, 的垂直平分线分别交 于 连接 ,则 的长为( ) A、 B、 C、 D、8. 如图,高速公路上有 、 两点相距 , 、 为两村庄,已知 , , 于 , 于 ,现要在 上建一个服务站 ,使得 、 两村庄到 站的距离相等,则 的长是( ) .
A、 B、 C、 D、8. 如图,高速公路上有 、 两点相距 , 、 为两村庄,已知 , , 于 , 于 ,现要在 上建一个服务站 ,使得 、 两村庄到 站的距离相等,则 的长是( ) .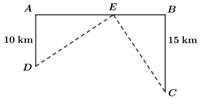 A、 B、 C、 D、9. 如图,小巷左、右两侧是竖直的墙壁,一架梯子斜靠在左墙上时,梯子底端到左墙角的距离为1米,梯子顶端距离地面3米.若梯子底端位置保持不动,将梯子斜靠在右墙上,此时梯子顶端距离地面2米,则小巷的宽度为 ( )
A、 B、 C、 D、9. 如图,小巷左、右两侧是竖直的墙壁,一架梯子斜靠在左墙上时,梯子底端到左墙角的距离为1米,梯子顶端距离地面3米.若梯子底端位置保持不动,将梯子斜靠在右墙上,此时梯子顶端距离地面2米,则小巷的宽度为 ( ) A、 米 B、3米 C、 米 D、2米10. 如图,斜靠在墙上的一根竹竿,AB=5m,OB=3m。若B端沿地面OB方向外移0.5m,则A端沿垂直于地面AC方向下移( )
A、 米 B、3米 C、 米 D、2米10. 如图,斜靠在墙上的一根竹竿,AB=5m,OB=3m。若B端沿地面OB方向外移0.5m,则A端沿垂直于地面AC方向下移( ) A、等于0.5m B、小于0.5m C、大于0.5m D、不确定11. 如图,圆柱形容器高为18cm,底面周长为32cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好也在杯内壁,离杯上沿2cm与蜂蜜正相对的点A处,则蚂蚁从内壁A处到达内壁B处的最短距离为( )
A、等于0.5m B、小于0.5m C、大于0.5m D、不确定11. 如图,圆柱形容器高为18cm,底面周长为32cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好也在杯内壁,离杯上沿2cm与蜂蜜正相对的点A处,则蚂蚁从内壁A处到达内壁B处的最短距离为( )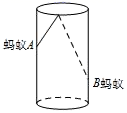 A、13cm B、 cm C、2 cm D、20cm12. 如图,长方形的长为15,宽为10,高为20,点 离点 的距离为5,蚂蚁如果要沿着长方形的表面从点 爬到点 ,需要爬行的最短距离是( )
A、13cm B、 cm C、2 cm D、20cm12. 如图,长方形的长为15,宽为10,高为20,点 离点 的距离为5,蚂蚁如果要沿着长方形的表面从点 爬到点 ,需要爬行的最短距离是( ) A、35 B、 C、25 D、13. 意大利文艺复兴时期的著名画家达•芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形 由两个正方形和两个全等的直角三角形组成.已知六边形 的面积为28, .小明将纸片②翻转后拼成如图2所示的图形,其中 ,则四边形 的面积为( )
A、35 B、 C、25 D、13. 意大利文艺复兴时期的著名画家达•芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形 由两个正方形和两个全等的直角三角形组成.已知六边形 的面积为28, .小明将纸片②翻转后拼成如图2所示的图形,其中 ,则四边形 的面积为( )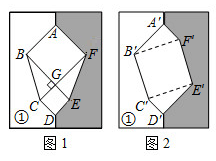 A、16 B、20 C、22 D、2414. 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 . 若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是( )
A、16 B、20 C、22 D、2414. 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 . 若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是( )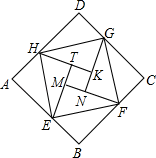 A、S1=2 B、S2=3 C、S3=6 D、S1+S3=815. 勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,已知∠BAC=90°,AB=6,AC=8,点D、E、F、G、H、I都在矩形KLMJ的边上,则矩形KLMJ的周长为( )
A、S1=2 B、S2=3 C、S3=6 D、S1+S3=815. 勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,已知∠BAC=90°,AB=6,AC=8,点D、E、F、G、H、I都在矩形KLMJ的边上,则矩形KLMJ的周长为( )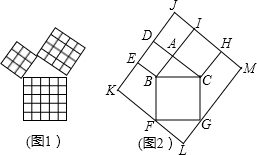 A、40 B、44 C、84 D、88
A、40 B、44 C、84 D、88二、填空题
-
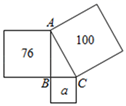
16. 如图,在 中,∠ABC=90°,分别以 的三边为边向外作正方形,其中两个正方形的面积分别为100,76.则字母a代表的正方形的面积是 .
 17. 如图,在边长为1的正方形网格中,两格点A , B之间的距离为d等于 .
17. 如图,在边长为1的正方形网格中,两格点A , B之间的距离为d等于 .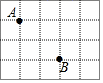 18. 如图,已知AB⊥BD , AB∥ED , AB=ED , 要证明ΔABC≌ΔEDC , 若以“SAS”为依据,还要添加的条件为;若添加条件AC=EC , 则可以用方法判定全等.
18. 如图,已知AB⊥BD , AB∥ED , AB=ED , 要证明ΔABC≌ΔEDC , 若以“SAS”为依据,还要添加的条件为;若添加条件AC=EC , 则可以用方法判定全等.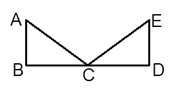 19. 如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是.(填SAS或AAS或HL)
19. 如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是.(填SAS或AAS或HL)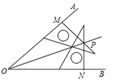 20. 如图,在Rt△ABC中,∠C=90°,M是BC上一点,过点M作MD⊥AB于点D,且MC=MD,如果AC=8,AB=10,那么BD=.
20. 如图,在Rt△ABC中,∠C=90°,M是BC上一点,过点M作MD⊥AB于点D,且MC=MD,如果AC=8,AB=10,那么BD=.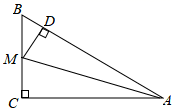 21. 如图, ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.若BE=6,CF=8,则 DEF的面积是
21. 如图, ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.若BE=6,CF=8,则 DEF的面积是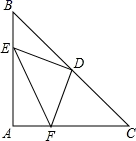 22. 如图,AP平分∠NAM,PC=PB,AB>AC,PD⊥AB于D,∠DPB=50°,则∠ACP的度数是.
22. 如图,AP平分∠NAM,PC=PB,AB>AC,PD⊥AB于D,∠DPB=50°,则∠ACP的度数是.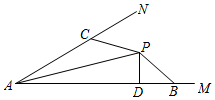 23. 如图,一只蚂蚁从实心长方体的顶点 出发,沿长方体的表面爬到对角顶点 处(三条棱长如图所示),问最短路线长为.
23. 如图,一只蚂蚁从实心长方体的顶点 出发,沿长方体的表面爬到对角顶点 处(三条棱长如图所示),问最短路线长为.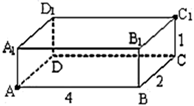 24. 如图,将边长为4的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,则BE的长为.
24. 如图,将边长为4的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,则BE的长为. 25. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 交于点O.若 ,则 .
25. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 交于点O.若 ,则 .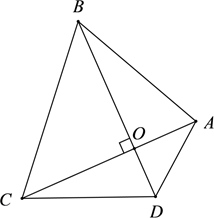
三、解答题
-
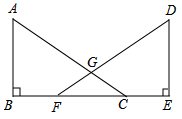
26. 已知:如图,点B,F,C,E在同一直线上, , 相交于点G, ,垂足为B, ,垂足为E,且 , .求证: .
 27. 如图,在 中, , ,分别以 、 为边在 的外侧作等边 和等边 ,连接 与 交于点F,若 ,求 的长是多少?
27. 如图,在 中, , ,分别以 、 为边在 的外侧作等边 和等边 ,连接 与 交于点F,若 ,求 的长是多少?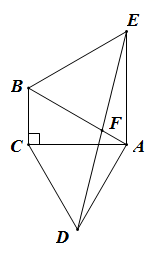
四、综合题
-
28. 如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE=4,AE=
 (1)、求AC、CE的长;(2)、求证:∠ACE=90°.29. 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.
(1)、求AC、CE的长;(2)、求证:∠ACE=90°.29. 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.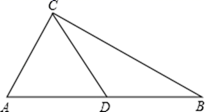 (1)、若 三边长分别是2, 和4,则此三角形常态三角形(填“是”或“不是”);(2)、若 是常态三角形,则此三角形的三边长之比为(请按从小到大排列);(3)、如图, 中,∠ACB=90°,BC=6,AD=DB=DC,若 是常态三角形,求 的面积.30. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,AB=10,CD=3.
(1)、若 三边长分别是2, 和4,则此三角形常态三角形(填“是”或“不是”);(2)、若 是常态三角形,则此三角形的三边长之比为(请按从小到大排列);(3)、如图, 中,∠ACB=90°,BC=6,AD=DB=DC,若 是常态三角形,求 的面积.30. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,AB=10,CD=3.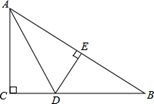 (1)、求DE的长(2)、求△BDE的面积.31. 已知:如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,BD=9.
(1)、求DE的长(2)、求△BDE的面积.31. 已知:如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,BD=9.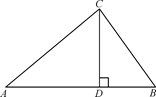 (1)、求CD的长.(2)、求AD的长.(3)、△ABC是直角三角形吗?请说明理由.32. 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)、求CD的长.(2)、求AD的长.(3)、△ABC是直角三角形吗?请说明理由.32. 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求: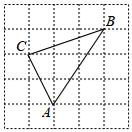 (1)、边AC、AB、BC的长;(2)、求△ABC的面积;(3)、点C到AB边的距离.33. 我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.(1)、特例感知
(1)、边AC、AB、BC的长;(2)、求△ABC的面积;(3)、点C到AB边的距离.33. 我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.(1)、特例感知等腰直角三角形勾股高三角形(请填写“是”或者“不是”);
(2)、如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若 ,试求线段CD的长度. (3)、深入探究
(3)、深入探究如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB , CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;
 (4)、推广应用
(4)、推广应用如图3,等腰△ABC为勾股高三角形,其中 ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E . 若 ,试求线段DE的长度.
 34.
34.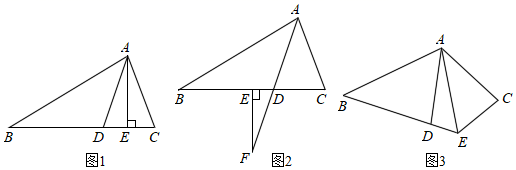 (1)、如图1,AD平分∠BAC , AE⊥BC , ∠B=30°,∠C=70°.∠BAC=°,∠DAE=°;(2)、如图2.若把“AE⊥BC”变成“点F在AD的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;(3)、如图3,AD平分∠BAC , AE平分∠BEC , ∠C﹣∠B=40°,求∠DAE的度数.35. 阅读材料:分析探索题:细心观察如图⑴,认真分析各式,然后解答问题.
(1)、如图1,AD平分∠BAC , AE⊥BC , ∠B=30°,∠C=70°.∠BAC=°,∠DAE=°;(2)、如图2.若把“AE⊥BC”变成“点F在AD的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;(3)、如图3,AD平分∠BAC , AE平分∠BEC , ∠C﹣∠B=40°,求∠DAE的度数.35. 阅读材料:分析探索题:细心观察如图⑴,认真分析各式,然后解答问题.;
;
……
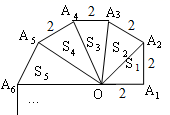 (1)、请用含有 ( 为正整数)的等式 ;(2)、推算出 .求出 …… 的值.36. 如图,在△ABC中,∠ACB=90°,BC=AC=6,D是AB边上任意一点,连接CD , 以CD为直角边向右作等腰直角△CDE , 其中∠DCE=90°,CD=CE , 连接BE .
(1)、请用含有 ( 为正整数)的等式 ;(2)、推算出 .求出 …… 的值.36. 如图,在△ABC中,∠ACB=90°,BC=AC=6,D是AB边上任意一点,连接CD , 以CD为直角边向右作等腰直角△CDE , 其中∠DCE=90°,CD=CE , 连接BE .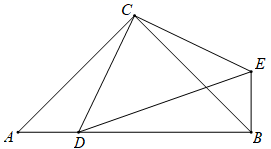 (1)、求证:AD=BE;(2)、当△CDE的周长最小时,求CD的值;(3)、求证: .37. 在平面直角坐标系中,点 , ,点C为x轴正半轴上一动点,过点A作 交y轴于点E.
(1)、求证:AD=BE;(2)、当△CDE的周长最小时,求CD的值;(3)、求证: .37. 在平面直角坐标系中,点 , ,点C为x轴正半轴上一动点,过点A作 交y轴于点E.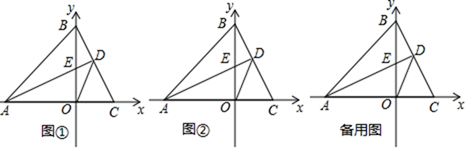 (1)、如图 ,若点C的坐标为(3,0),试求点E的坐标;(2)、如图 ,若点C在x轴正半轴上运动,且 ,其它条件不变,连接DO,求证:OD平分(3)、若点C在x轴正半轴上运动,当 时,试探索线段AD、OC、DC的数量关系,并证明.38. 教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为 ,较小的直角边长都为 ,斜边长都为 ),大正方形的面积可以表示为 ,也可以表示为 ,由此推导出重要的勾股定理:如果直角三角形两条直角边长为 ,斜边长为 ,则 .
(1)、如图 ,若点C的坐标为(3,0),试求点E的坐标;(2)、如图 ,若点C在x轴正半轴上运动,且 ,其它条件不变,连接DO,求证:OD平分(3)、若点C在x轴正半轴上运动,当 时,试探索线段AD、OC、DC的数量关系,并证明.38. 教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为 ,较小的直角边长都为 ,斜边长都为 ),大正方形的面积可以表示为 ,也可以表示为 ,由此推导出重要的勾股定理:如果直角三角形两条直角边长为 ,斜边长为 ,则 . (1)、图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.(2)、如图③,在 中, 是 边上的高, , , ,设 ,求 的值.(3)、试构造一个图形,使它的面积能够解释 ,画在如图4的网格中,并标出字母 所表示的线段.39. 如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)、图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.(2)、如图③,在 中, 是 边上的高, , , ,设 ,求 的值.(3)、试构造一个图形,使它的面积能够解释 ,画在如图4的网格中,并标出字母 所表示的线段.39. 如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.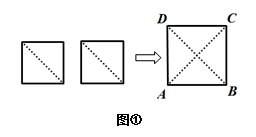
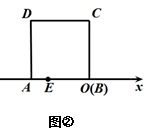 (1)、正方形ABCD的面积为 , 边长为 , 对角线BD=;(2)、求证: ;(3)、如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 , 若点E所表示的数为整数,则点E所表示的数为40. 综合与实践:
(1)、正方形ABCD的面积为 , 边长为 , 对角线BD=;(2)、求证: ;(3)、如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 , 若点E所表示的数为整数,则点E所表示的数为40. 综合与实践:如图1, 中, , 于点 , 且 ;如图2,在图1的基础上,动点 从点 出发以每秒 的速度沿线段 向点 运动,同时动点 从点 出发以相同速度沿线段 向点 运动,当其中一点到达终点时另外一点也随之停止运动,设点 运动的时间为 秒.
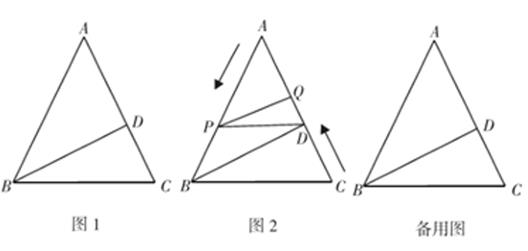 (1)、求 的长;(2)、当 的其中一边与 平行时( 与 不重合),求 的值;(3)、点 在线段 上运动的过程中,是否存在以 为腰的 是等腰三角形?若存在,求出 的值;若不存在,请说明理由.
(1)、求 的长;(2)、当 的其中一边与 平行时( 与 不重合),求 的值;(3)、点 在线段 上运动的过程中,是否存在以 为腰的 是等腰三角形?若存在,求出 的值;若不存在,请说明理由.