初中数学浙教版八年级上学期期末培优专题2 等腰三角形
试卷更新日期：2020-11-26 类型：复习试卷
一、单选题
-
1. 等腰 中， ，若 ，则 的度数是（ ）A、 B、 C、 D、2. 若 与 关于直线 对称，且 垂直平分 ，则一定有（ ）A、 B、 C、 D、3. 如图，在平面直角坐标系中，点A的坐标为 ，在x轴上确定点P，使 为等腰三角形，则符合条件的点P有（ ）
A、2个 B、3个 C、4个 D、5个4. 如图，在△ABC中，BF、CF分别平分∠ABC和∠ACB ， 过点F作EG∥BC分别交于点AB、AC于点E、G ． 若AB=9，BC=10，AC=11，则△AEG的周长为（ ）
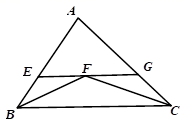A、15 B、20 C、21 D、195. 等腰三角形的周长为 ，其中一边长为 ，则该等腰三角形的底边长为（ ）A、 B、 C、 D、 或6. 如图，把长方形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么，有下列说法：①△EBD是等腰三角形，EB=ED；②折叠后∠ABE和∠CBD一定相等；③△EBA和△EDC一定是全等三角形.其中正确的有（ ）
A、0个 B、1个 C、2个 D、3个7. 如图， ABC和 关于直线L对称，下列结论：① ABC≌ ；②∠BAC＝ ；③直线L垂直平分 ；④直线L平分 .正确的有（ ）
A、4个 B、3个 C、2个 D、1个8. 如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE＝2BF，给出下列四个结论：①DE＝DF；②DB＝DC；③AD⊥BC；④AC＝3BF，其中正确的结论共有（ ）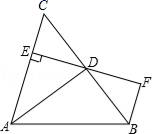
A、①②③④ B、①②④ C、①②③ D、②③④9. 如图，在△ABC中，AC=AB，∠BAC=90°，BD平分∠ABC，与AC相交于点F，CD⊥BD，垂足为D，交BA的延长线于点E，AH⊥BC交BD于点M，交BC于点H，下列选项不正确的是（ ）
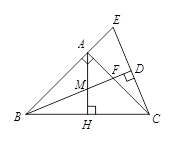A、∠E＝67.5 B、∠AMF＝∠AFM C、BF＝2CD D、BD＝AB+AF10. 如图，在△ABC中，BD、CE分别是∠ABC和∠ACB的平分线，AM⊥CE于P，交BC于M，AN⊥BD于Q，交BC于N，∠BAC＝110°，AB＝6，AC＝5，MN＝2，结论①AP＝MP；②BC＝9；③∠MAN＝35°；④AM＝AN.其中不正确的有（ ）
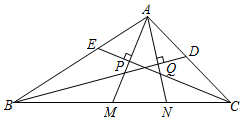A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 已知等腰三角形 ， ，D为 边上一点，且 和 都是等腰三角形，则 ．12. 如图所示，在 中， ， ，AB的垂直平分线交AB于点D ， 交AC于点E ， 连接BE ， 则 的度数为（）
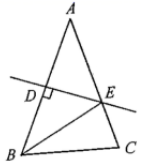13. 如图，已知点P是射线ON上一动点（即P可在射线ON上运动），∠AON=45°，当∠A=时，△AOP为等腰三角形.
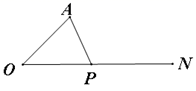14. 如图，在边长为1的小正方形组成的网格中，四边形ABCD的四个顶点都在格点上，请按要求完成下列各题.
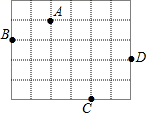(1)、线段AB的长为__，BC的长为__，CD的长为__，AD的长为__；(2)、连接AC，通过计算△ACD的形状是；△ABC的形状是.15. 如图，在正方形网格中有两个小正方形被涂黑，再涂黑一个图中其余的小正方形，使得整个被涂黑的图案构成一个轴对称图形，那么涂法共有种.
16. 阅读后填空：已知：如图，∠A＝∠D＝90°，AC＝DB，AC、DB相交于点O.
求证：OA＝OD.
分析：要证OA＝OD，可证 ABO≌ DCO；
要证 ABO≌ DCO，可先证 ABC≌ DCB得出AB＝DC这个结论；
而用可证 ABC≌ DCB（填SAS或AAS或HL）.
17. 如图， ABC中，∠C＝90°，点A关于BC边的对称点为 ，点B关于AC边的对称点为 ，点C关于AB边的对称点为 ， ABC与 的面积之比为.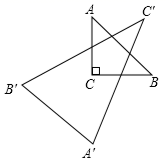
18. 如图，∠AOB是一角度为15°的钢架，要使钢架更加牢固，需在其内部添加一些钢管：EF、FG、GH…，且OE=EF=FG=GH…，在OA、OB足够长的情况下，最多能添加这样的钢管的根数为.
19. 如图，在 中，AB=AC=10，BC=12，AD=8，AD⊥BC.若P、Q分别是AD和AC上的动点，则PC+PQ的最小值是.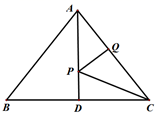
20. 已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（10，0）、C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为 ．
三、计算题
-
21. 如图，在平面直角坐标系中，△ABC的顶点A，B，C均在正方形网格的格点上.
(1)、画出△ABC关于y轴的对称图形△A1B1C1；(2)、直接写出△A1B1C1各个顶点的坐标.22. 如图． 平分 ， ，垂足为E， 交 的延长线于点F，若 恰好平分 ．求证：
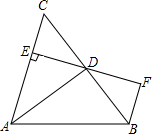(1)、点D为 的中点；(2)、 ．四、解答题
-
23. 如图，已知AD=BC，AC=BD，求证：OD=OC.
24. 已知：如图∠ABC＝∠ADC＝90°，M、N分别是AC、BD的中点.求证：MN⊥BD.
五、综合题
-
25. 如图，在 中，点 分别在边 上，连接 ，且 ．
(1)、证明： ；(2)、若 ，当点D在 上运动时（点D不与 重合），且 是等腰三角形，求此时 的长．26. 在 ABC中，AB边的垂直平分线l1交BC于D，AC边的垂直平分线l2交BC于E，l1与l2相交于点O. ADE的周长为8cm.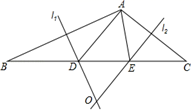
(1)、求BC的长；(2)、若∠BAC＝128°，求∠DAE的度数是多少？(3)、分别连结OA、OB、OC，若 OBC的周长为18cm，求OA的长.27. 如图1，△ABC 中，AB＝AC，点 D 在 AB 边上，点 E 在 AC 的延长线上，且 CE＝BD， 连接 DE 交 BC 于点 F．
(1)、求证：EF＝DF；(2)、如图2，过点 D 作 DG⊥BC，垂足为 G，求证：BC＝2FG.28. 在 中，AB=AC，点D是直线BC上一点(不与B、C重合)，以AD为一边在AD的右侧作 ，使AD=AE，∠DAE=∠BAC，连接CE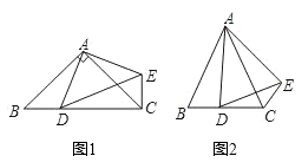
(1)、如图1，当点D在线段BC上，且∠BAC=90°.①说明： ；
②线段CE、CD、BC的数量关系为_▲_.
(2)、如图2，当点D在直线BC上，设∠BAC=α，∠BCE=β.则α，β之间有怎样的数量关系？请直接写出你的结论.29. 如图
(1)、如图（1），已知CE与AB交于点E，AC=BC，∠1=∠2.求证： .(2)、如图（2），已知CD的延长线与AB交于点E，AD=BC，∠3=∠4.探究AE与BE的数量关系，并说明理由.30. 问题提出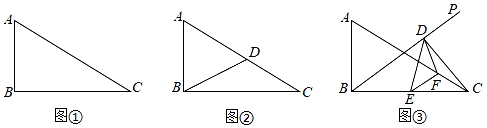
(1)、如图①，在Rt△ABC中，∠ABC＝90°，AB＝12，BC＝16，则AC＝；问题探究
(2)、如图②，在Rt△ABC中，∠ABC＝90°，AC＝10，点D是AC边上一点，且满足DA＝DB，则CD＝；问题解决
(3)、如图③，在Rt△ABC中，过点B作射线BP，将∠C折叠，折痕为EF，其中E为BC中点，点F在AC边上，点C的对应点落在BP上的点D处，连接ED、FD，若BC＝8，求△BCD面积的最大值，及面积最大时∠BCD的度数.31. 已知点A(8，0)及在第一象限的动点B(x，y)，且x+y＝10，设 OBA的面积为S．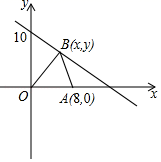
(1)、求S关于x的函数关系式，并写出自变量x的取值范围；(2)、求S＝12时B点坐标；(3)、在（2）的基础上，设点Q为y轴上一动点，当BQ+AQ的值最小时，求Q点坐标．32. 如图， ABC和 DEF是两个等腰直角三角形，∠BAC=∠DFE=90°，AB=AC，FD=FE， DEF的顶点E在边BC上移动，在移动过程中，线段DE与线段AB相交于点P，线段EF与线段CA相交于点Q．
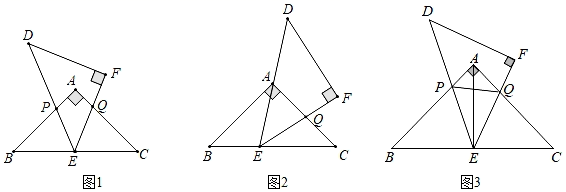(1)、如图1，当E为BC中点，且BP=CQ时，求证：△BPE≌△CQE；(2)、如图2，当ED经过点A，且BE=CQ时，求∠EAQ的度数；(3)、如图3，当E为BC中点，连接AE、PQ，若AP=3，AQ=4，PQ=5，求AC的长．33. 如图，在△ABC中，AB＝AC，∠BAC＝80°，点D为△ABC内一点，∠ABD＝∠ACD＝20°，E为BD延长线上的一点，且AB＝AE.
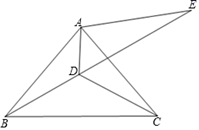(1)、求∠BAD的度数；(2)、求证：DE平分∠ADC；(3)、请判断AD，BD，DE之间的数量关系，并说明理由.34. 如图1，已知直线l的同侧有两个点A，B，在直线l上找一点P，使P点到A，B两点的距离之和最短的问题，可以通过轴对称来确定，即作出其中一点关于直线l的对称点，对称点与另一点的连线与直线l的交点就是所要找的点，通过这种方法可以求解很多问题
(1)、如图2，在平面直角坐标系内，点A的坐标为(1，1)，点B的坐标为(5，4)，动点P在x轴上，求PA+PB的最小值；(2)、如图3，在锐角三角形ABC中，AB=8，∠BAC=45°，∠BAC的角平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值为(3)、如图4，∠AOB=30°，OC=4，OD=10，点E，F分别是射线OA，OB上的动点，则CF+EF+DE的最小值为。35. 如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，△CDE是等边三角形，点D在边AB上.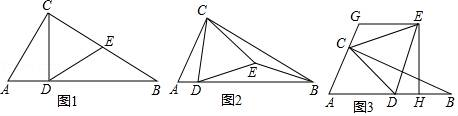
(1)、如图1，当点E在边BC上时，求证DE＝EB；(2)、如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；(3)、如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG＝5CG，BH＝3.求CG的长.