初中数学浙教版八年级上学期期末培优专题1 三角形
试卷更新日期:2020-11-26 类型:复习试卷
一、单选题
-
1. 已知,在 与 中, ,那么添加一个条件后,仍无法判定 的是( )A、 B、 C、 D、 与 的周长相等2. 等腰三角形的两边长为2和6,则周长是( )A、10 B、14 C、10或14 D、63. 如图, 顶角为120°, , ,现将 折叠,使点B与点A重合,折痕为 ,则DE的长为( )
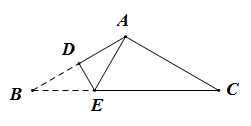 A、1 B、2 C、 D、4. 如图,Rt△ABC中,∠A=90°,∠ABC=56°,将△ABC沿着DE翻折,使得点C恰好与点B重合,连接BE , 则∠AEB的度数为( )
A、1 B、2 C、 D、4. 如图,Rt△ABC中,∠A=90°,∠ABC=56°,将△ABC沿着DE翻折,使得点C恰好与点B重合,连接BE , 则∠AEB的度数为( )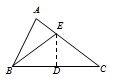 A、68° B、58° C、22° D、34°5. 若等腰三角形的两边长分别为5cm和10cm,则此三角形的周长是( )A、15cm B、20cm C、25cm D、20cm或25cm6. 如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为( )
A、68° B、58° C、22° D、34°5. 若等腰三角形的两边长分别为5cm和10cm,则此三角形的周长是( )A、15cm B、20cm C、25cm D、20cm或25cm6. 如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为( )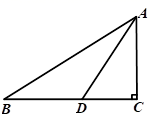 A、13 B、14 C、15 D、217. 如图,在 中, , 平分 交 于点D, 于点E,下列结论中正确的个数是( ).
A、13 B、14 C、15 D、217. 如图,在 中, , 平分 交 于点D, 于点E,下列结论中正确的个数是( ).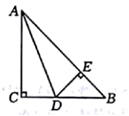
① 平分 :② ;③ 平分 ;④ .
A、3个 B、2个 C、1个 D、4个8. 在如图所示的 6×6 网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数( )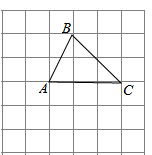 A、3 个 B、4 个 C、6 个 D、7 个9. 如图,在 直角△ABC中, ,AB=AC , 点D为BC中点,直角 绕点D旋转,DM , DN分别与边AB , AC交于E , F两点,下列结论:①△DEF是等腰直角三角形;② AE=CF;③△BDE≌△ADF;④ BE+CF=EF , 其中正确结论是( )
A、3 个 B、4 个 C、6 个 D、7 个9. 如图,在 直角△ABC中, ,AB=AC , 点D为BC中点,直角 绕点D旋转,DM , DN分别与边AB , AC交于E , F两点,下列结论:①△DEF是等腰直角三角形;② AE=CF;③△BDE≌△ADF;④ BE+CF=EF , 其中正确结论是( )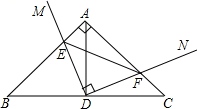 A、①②④ B、②③④ C、①②③ D、①②③④10. 如图,四边形ABCD中,∠A=90°,AD=2,连接BD , BD⊥CD , 垂足是D且∠ADB=∠C , 点P是边BC上的一动点,则DP的最小值是( )
A、①②④ B、②③④ C、①②③ D、①②③④10. 如图,四边形ABCD中,∠A=90°,AD=2,连接BD , BD⊥CD , 垂足是D且∠ADB=∠C , 点P是边BC上的一动点,则DP的最小值是( )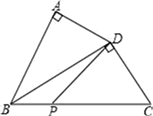 A、1 B、1.5 C、2 D、2.5
A、1 B、1.5 C、2 D、2.5二、填空题
-
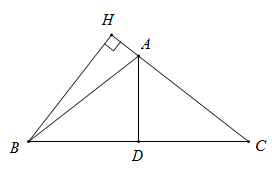
11. △ABC中,三边之比为3:4:5,且最长边为10m , 则△ABC周长为cm .12. 如图, 是钝角三角形 的高, 是角平分线,且 ,若 , 的面积为12,则 .
 13. 如图,在△ABC中,∠B=38°,∠C=40°,AB的垂直平分线交BC于D , AC的垂直平分线交BC于E , 则∠DAE= ° .
13. 如图,在△ABC中,∠B=38°,∠C=40°,AB的垂直平分线交BC于D , AC的垂直平分线交BC于E , 则∠DAE= ° .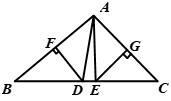 14. 如图,在△ABC中,AD,CE分别为BC,AB边上的高,若BC=6,AD=5,CE=4,则AB的长为 .
14. 如图,在△ABC中,AD,CE分别为BC,AB边上的高,若BC=6,AD=5,CE=4,则AB的长为 . 15. 已知三角形的三边长分别为4,8,a,则a的取值范围是 .16. 如图,OP平分∠AOB,PA OA,PB OB,垂足分别为点A、B.下列结论中,一定成立的是(填序号)
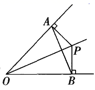
15. 已知三角形的三边长分别为4,8,a,则a的取值范围是 .16. 如图,OP平分∠AOB,PA OA,PB OB,垂足分别为点A、B.下列结论中,一定成立的是(填序号)①PA=PB;②OA=OB;③OP垂直平分AB;④AB垂直平分OP
 17. 如图, ABC中,∠C=90°,点A关于BC边的对称点为 ,点B关于AC边的对称点为 ,点C关于AB边的对称点为 , ABC与 的面积之比为.
17. 如图, ABC中,∠C=90°,点A关于BC边的对称点为 ,点B关于AC边的对称点为 ,点C关于AB边的对称点为 , ABC与 的面积之比为.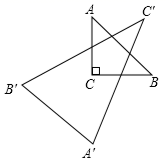 18. 如图, AB = 4cm , AC = BD = 3cm . ∠CAB = ∠DBA ,点 P 在线段 AB 上以1cm / s 的速度由点 A 向点 B 运动,同时,点Q 在线段 BD 上由点 B 向点 D 运动.设运动时间为t(s) , 则当点Q 的运动速度为cm / s 时, DACP 与DBPQ 全等.
18. 如图, AB = 4cm , AC = BD = 3cm . ∠CAB = ∠DBA ,点 P 在线段 AB 上以1cm / s 的速度由点 A 向点 B 运动,同时,点Q 在线段 BD 上由点 B 向点 D 运动.设运动时间为t(s) , 则当点Q 的运动速度为cm / s 时, DACP 与DBPQ 全等. 19. 如图,有一个直角三角形ABC,∠C=90°,AC ,BC ,线段PQ AB,点Q在过点A且垂直于AC的射线AX上来回运动,点P从C点出发,沿射线CA以 的速度运动,问P点运动 秒时 t ,才能使
19. 如图,有一个直角三角形ABC,∠C=90°,AC ,BC ,线段PQ AB,点Q在过点A且垂直于AC的射线AX上来回运动,点P从C点出发,沿射线CA以 的速度运动,问P点运动 秒时 t ,才能使 ABC≌
ABC≌  QPA全等.
QPA全等. 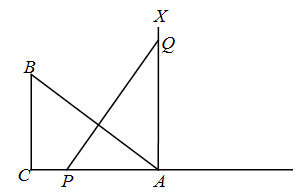 20. 如图,△ABC≌△ADE,BC的延长线交DE于点G.若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB=.
20. 如图,△ABC≌△ADE,BC的延长线交DE于点G.若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB=.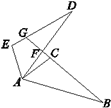
三、计算题
-
21. 如图. 平分 , ,垂足为E, 交 的延长线于点F,若 恰好平分 .求证:
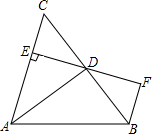 (1)、点D为 的中点;(2)、 .22. 已知 为三角形三边的长, 化简: .23. 如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A,B,C的距离分别为3,4,5,求∠AEB的度数.
(1)、点D为 的中点;(2)、 .22. 已知 为三角形三边的长, 化简: .23. 如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A,B,C的距离分别为3,4,5,求∠AEB的度数.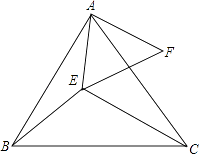 24. 如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
24. 如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.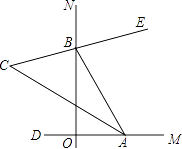
四、解答题
-
25. 如图,在△ABC中,AB=AC,∠B=30°,D为BC边上一点,∠DAB=45°.
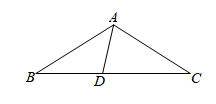 (1)、求∠DAC的度数;(2)、请说明:AB=CD.26. 如图:AB=CD,AE=DF,CE=FB.求证:AF=DE.
(1)、求∠DAC的度数;(2)、请说明:AB=CD.26. 如图:AB=CD,AE=DF,CE=FB.求证:AF=DE. 27. 如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,∠EAB=105°,求∠BFD和∠BED的度数.
27. 如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,∠EAB=105°,求∠BFD和∠BED的度数.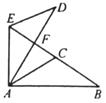
五、综合题
-
28. 已知, 中, 于点 , .
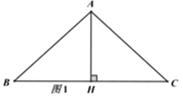
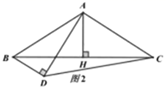
 (1)、如图1,求证: ;(2)、如图2,点D为 外一点, ,若 平分 ,求证: ;(3)、如图3,在(2)的条件下,若 , ,求 的面积.29. 在 中,点D、E在 边上,满足 , ,且 .(1)、如图1,求证: ;
(1)、如图1,求证: ;(2)、如图2,点D为 外一点, ,若 平分 ,求证: ;(3)、如图3,在(2)的条件下,若 , ,求 的面积.29. 在 中,点D、E在 边上,满足 , ,且 .(1)、如图1,求证: ; (2)、如图2,过点E作 交 于点G,交 于点F,求证: ;
(2)、如图2,过点E作 交 于点G,交 于点F,求证: ;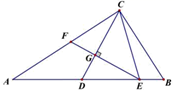 (3)、如图3,在(2)的条件下,当点F为 中点时,求 的值.
(3)、如图3,在(2)的条件下,当点F为 中点时,求 的值. 30. 如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.
30. 如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.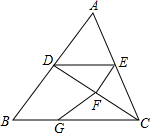 (1)、求证:ED∥BC;(2)、若D,E,F分别是AB,AC,CD边上的中点,四边形ADFE的面积为6.
(1)、求证:ED∥BC;(2)、若D,E,F分别是AB,AC,CD边上的中点,四边形ADFE的面积为6.①求△ABC的面积;
②若G是BC边上一点,CG=2BG,求△FCG的面积.
31. 如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与点C重合,点D与点G重合,若BC=8,AB=4,求: (1)、求CF的长.(2)、求EF的长.(3)、求阴影部分△GED的面积.32. 现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
(1)、求CF的长.(2)、求EF的长.(3)、求阴影部分△GED的面积.32. 现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.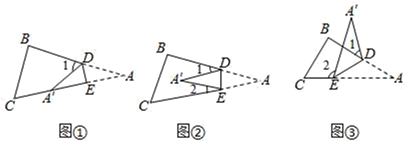 (1)、如果折成图①的形状,使点A落在CE上,则∠1与∠A的数量关系是 .(2)、如果折成图②的形状,猜想∠1+∠2与∠A的数量关系是;(3)、如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.33. 如图,线段AB=4,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
(1)、如果折成图①的形状,使点A落在CE上,则∠1与∠A的数量关系是 .(2)、如果折成图②的形状,猜想∠1+∠2与∠A的数量关系是;(3)、如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.33. 如图,线段AB=4,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).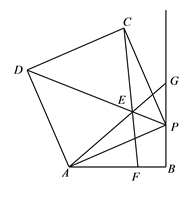 (1)、求证: AEP≌ CEP;(2)、判断CF与AB的位置关系,并说明理由;(3)、请直接写出 AEF的周长.34. 已知:如图,△ABC中∠ACB的平分线与AB的垂直平分线交于点D,DE⊥AC于点E,DF⊥BC交CB的延长线于点F.
(1)、求证: AEP≌ CEP;(2)、判断CF与AB的位置关系,并说明理由;(3)、请直接写出 AEF的周长.34. 已知:如图,△ABC中∠ACB的平分线与AB的垂直平分线交于点D,DE⊥AC于点E,DF⊥BC交CB的延长线于点F.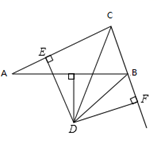 (1)、求证:AE=BF;(2)、若AC=24,BC=10,求AE的长.35. 在 中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作 ,使AD=AE,∠DAE=∠BAC,连接CE
(1)、求证:AE=BF;(2)、若AC=24,BC=10,求AE的长.35. 在 中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作 ,使AD=AE,∠DAE=∠BAC,连接CE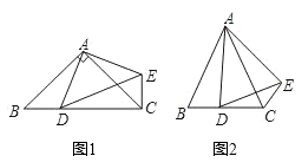 (1)、如图1,当点D在线段BC上,且∠BAC=90°.
(1)、如图1,当点D在线段BC上,且∠BAC=90°.①说明: ;
②线段CE、CD、BC的数量关系为_▲_.
(2)、如图2,当点D在直线BC上,设∠BAC=α,∠BCE=β.则α,β之间有怎样的数量关系?请直接写出你的结论.