广西壮族自治区玉林市北流市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-26 类型:期末考试
一、单选题
-
1. 3的倒数是( )A、 3 B、-3 C、 D、2. 下列图形中,∠1与∠2是同旁内角的是( )A、
 B、
B、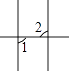 C、
C、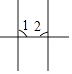 D、
D、 3. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总 人口为4400000000人,这个数用科学记数法表示为( )A、4.4×108 B、4.40×108 C、4.4×109 D、4.4×10104. 在 中, ,点 , 分别是边 , 的中点,点 在 内,连接 , , .以下图形符合上述描述的是( )A、
3. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总 人口为4400000000人,这个数用科学记数法表示为( )A、4.4×108 B、4.40×108 C、4.4×109 D、4.4×10104. 在 中, ,点 , 分别是边 , 的中点,点 在 内,连接 , , .以下图形符合上述描述的是( )A、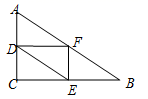 B、
B、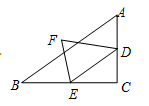 C、
C、 D、
D、 5. 如图,数轴上 , , , 四点中,能表示 点的是( )
5. 如图,数轴上 , , , 四点中,能表示 点的是( )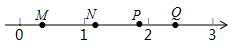 A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 下列几何图形不是中心对称图形的是( )A、平行四边形 B、正五边形 C、正方形 D、正六边形8. 如图,AD是半圆O的直径,AD=12,B,C是半圆O上两点.若 ,则图中阴影部分的面积是( )
A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 下列几何图形不是中心对称图形的是( )A、平行四边形 B、正五边形 C、正方形 D、正六边形8. 如图,AD是半圆O的直径,AD=12,B,C是半圆O上两点.若 ,则图中阴影部分的面积是( ) A、6π B、12π C、18π D、24π9. 如图,正方形网格中,每个小正方形的边长均为1个单位长度. , 在格点上,现将线段 向下平移 个单位长度,再向左平移 个单位长度,得到线段 ,连接 , .若四边形是正方形 ,则 的值是( )
A、6π B、12π C、18π D、24π9. 如图,正方形网格中,每个小正方形的边长均为1个单位长度. , 在格点上,现将线段 向下平移 个单位长度,再向左平移 个单位长度,得到线段 ,连接 , .若四边形是正方形 ,则 的值是( )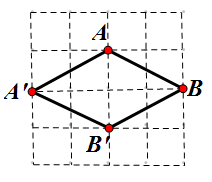 A、3 B、4 C、5 D、610. 若数据 , ,…, 的众数为 ,方差为 ,则数据 , ,…, 的众数、方差分别是( )A、 , B、 , C、 , D、 ,11. 如图, 是矩形 内的任意一点,连接 、 、 、 , 得到 , , , ,设它们的面积分别是 , , , , 给出如下结论:① ② ③若 ,则 ④若 ,则 点在矩形的对角线上.其中正确的结论的序号是( )
A、3 B、4 C、5 D、610. 若数据 , ,…, 的众数为 ,方差为 ,则数据 , ,…, 的众数、方差分别是( )A、 , B、 , C、 , D、 ,11. 如图, 是矩形 内的任意一点,连接 、 、 、 , 得到 , , , ,设它们的面积分别是 , , , , 给出如下结论:① ② ③若 ,则 ④若 ,则 点在矩形的对角线上.其中正确的结论的序号是( )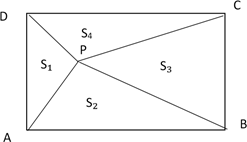 A、①② B、②③ C、③④ D、②④12. 若点 是直线 上一点,已知 ,则 的最小值是( )A、4 B、 C、 D、2
A、①② B、②③ C、③④ D、②④12. 若点 是直线 上一点,已知 ,则 的最小值是( )A、4 B、 C、 D、2二、填空题
-
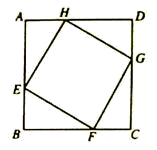
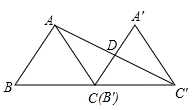
13. 计算: .14. 分解因式:3a2b+6ab2=.15. 若代数式5x-5与2x-9的值互为相反数,则x=.16. 从5,6,7这三个数字中,随机抽取两个不同数字组成一个两位数, 则这个两位数能被3整除的概率是.17. 如图,已知 的面积为48,将 沿 平移到 ,使 和 重合,连结 交 于 ,则 的面积为.
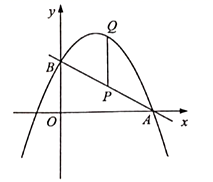
 18. 如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为
18. 如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为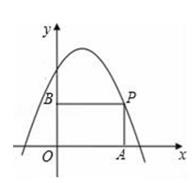
三、解答题
-
19. 计算: .20. 先化简.再求值( )÷ ,其中x满足x2﹣x﹣1=0.21. 已知关于 的方程: .(1)、求证:不论 取何实数,该方程都有两个不相等的实数根.(2)、设方程的两根为 , ,若 ,求 的值.22. 某校组织了一次七年级科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品,C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
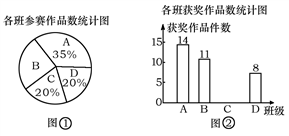 (1)、B班参赛作品有多少件?(2)、请你将图②的统计图补充完整;(3)、通过计算说明,哪个班的获奖率高?23. 如图, 为等腰三角形, , 是底边 的中点, 与腰 相切于点 .
(1)、B班参赛作品有多少件?(2)、请你将图②的统计图补充完整;(3)、通过计算说明,哪个班的获奖率高?23. 如图, 为等腰三角形, , 是底边 的中点, 与腰 相切于点 . (1)、求证: 与 相切;(2)、已知 , ,求 的半径.24. 某化工厂要在规定时间内搬运1200吨化工原料.现有 , 两种机器人可供选择,已知 型机器人比 型机器人每小时多搬运30吨型, 机器人搬运900吨所用的时间与 型机器人搬运600吨所用的时间相等.(1)、求两种机器人每小时分别搬运多少吨化工原料.(2)、该工厂原计划同时使用这两种机器人搬运,工作一段时间后, 型机器人又有了新的搬运任务需离开,但必须保证这批化工原料在11小时内全部搬运完毕.问 型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成?
(1)、求证: 与 相切;(2)、已知 , ,求 的半径.24. 某化工厂要在规定时间内搬运1200吨化工原料.现有 , 两种机器人可供选择,已知 型机器人比 型机器人每小时多搬运30吨型, 机器人搬运900吨所用的时间与 型机器人搬运600吨所用的时间相等.(1)、求两种机器人每小时分别搬运多少吨化工原料.(2)、该工厂原计划同时使用这两种机器人搬运,工作一段时间后, 型机器人又有了新的搬运任务需离开,但必须保证这批化工原料在11小时内全部搬运完毕.问 型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成?