广西壮族自治区南宁市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-26 类型:期末考试
一、单选题
-
1. 下列图形中的角是圆周角的是( )A、
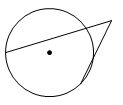 B、
B、 C、
C、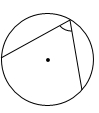 D、
D、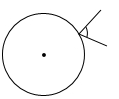 2. 一元二次方程 的一次项系数是( )A、2 B、3 C、-3 D、-13. 下列事件中,是必然事件的是( )A、经过有交通信号灯的路口,遇到红灯 B、明天太阳从西方升起 C、三角形内角和是 D、购买一张彩票,中奖4. 如图,四边形 内接于 , 为 延长线上一点,若 ,则 的度数为( )
2. 一元二次方程 的一次项系数是( )A、2 B、3 C、-3 D、-13. 下列事件中,是必然事件的是( )A、经过有交通信号灯的路口,遇到红灯 B、明天太阳从西方升起 C、三角形内角和是 D、购买一张彩票,中奖4. 如图,四边形 内接于 , 为 延长线上一点,若 ,则 的度数为( ) A、 B、 C、 D、5. 下列各点在抛物线 上的是( )A、 B、 C、 D、6. 不透明袋子中有 个红球和 个白球,这些球除颜色外无其他差别,从袋中随机取出 个球,是红球的概率是( )A、 B、 C、 D、7. 时钟上的分针匀速旋转一周需要60分钟,则经过10分钟,分针旋转了( ).A、10° B、20° C、30° D、60°8. 将抛物线 向左平移4个单位长度,再向.上平移1个单位长度得到的抛物线的解析式为( )A、 B、 C、 D、9. 已知关于 的一元二次方程 有一个根为1,则另一个根为( )A、 B、 C、 D、-110. 某公司2017年的营业额是100万元,2019年的营业额为121万元,设该公司年营业额的平均增长率为 ,根据题意可列方程为( )A、 B、 C、 D、11. 如图,正方形 的边长为 ,对角线 相交于点 ,将直角三角板的直角顶点放在点 处,两直角边分别与 重叠,当三角板绕点 顺时针旋转 角 时,两直角边与正方形的边 交于 两点,则四边形 的周长( )
A、 B、 C、 D、5. 下列各点在抛物线 上的是( )A、 B、 C、 D、6. 不透明袋子中有 个红球和 个白球,这些球除颜色外无其他差别,从袋中随机取出 个球,是红球的概率是( )A、 B、 C、 D、7. 时钟上的分针匀速旋转一周需要60分钟,则经过10分钟,分针旋转了( ).A、10° B、20° C、30° D、60°8. 将抛物线 向左平移4个单位长度,再向.上平移1个单位长度得到的抛物线的解析式为( )A、 B、 C、 D、9. 已知关于 的一元二次方程 有一个根为1,则另一个根为( )A、 B、 C、 D、-110. 某公司2017年的营业额是100万元,2019年的营业额为121万元,设该公司年营业额的平均增长率为 ,根据题意可列方程为( )A、 B、 C、 D、11. 如图,正方形 的边长为 ,对角线 相交于点 ,将直角三角板的直角顶点放在点 处,两直角边分别与 重叠,当三角板绕点 顺时针旋转 角 时,两直角边与正方形的边 交于 两点,则四边形 的周长( ) A、先变小再变大 B、先变大再变小 C、始终不变 D、无法确定12. 如图,抛物线 与 轴交于点 ,与 轴的负半轴交于点 ,点 是对称轴上的一个动点.连接 ,当 最大时,点 的坐标是( )
A、先变小再变大 B、先变大再变小 C、始终不变 D、无法确定12. 如图,抛物线 与 轴交于点 ,与 轴的负半轴交于点 ,点 是对称轴上的一个动点.连接 ,当 最大时,点 的坐标是( )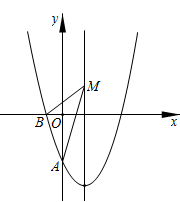 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知 的半径 点 在 内,则 (填>或=,<)14. 点 关于原点的对称点的坐标为.15. 如图,从一块直径是 的圆形铁皮上剪出一个圆心角是 的扇形,如果将剪下来的扇形围成一个圆锥,那么圆锥的底面圆的半径为 .
 16. 如图,二次函数 的图象与y轴交于点C,与x轴的一个交点为 ,点B在抛物线上,且与点C关于抛物线的对称轴对称.已知一次函数 的图象经过 两点,根据图象,则满足不等式 的x的取值范围是
16. 如图,二次函数 的图象与y轴交于点C,与x轴的一个交点为 ,点B在抛物线上,且与点C关于抛物线的对称轴对称.已知一次函数 的图象经过 两点,根据图象,则满足不等式 的x的取值范围是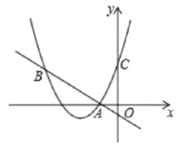 17. 在矩形 中, 点 是 边上的一个动点,连接 ,过点 作 与点 ,交射线 于点 ,连接 ,则 的最小值是
17. 在矩形 中, 点 是 边上的一个动点,连接 ,过点 作 与点 ,交射线 于点 ,连接 ,则 的最小值是
三、解答题
-
18. 如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,并且CD=4,EM=6,求⊙O的半径.
 19. 计算:4+(-2)2×2-(-36)÷420. 解方程21. 在下列网格图中,每个小正方形的边长均为 个单位 中, , 且 三点均在格点上.
19. 计算:4+(-2)2×2-(-36)÷420. 解方程21. 在下列网格图中,每个小正方形的边长均为 个单位 中, , 且 三点均在格点上. (1)、画出 绕 顺时针方向旋转 后的图形 ;(2)、求点 运动路径的长(结果保留 ) .22. 某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级(2)班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
(1)、画出 绕 顺时针方向旋转 后的图形 ;(2)、求点 运动路径的长(结果保留 ) .22. 某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级(2)班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:八年级(2)班参加球类活动人数情况统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
八年级(2)班学生参加球类活动人数情况扇形统计图
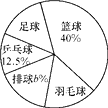
根据图中提供的信息,解答下列问题:
(1)、a= , b= .(2)、该校八年级学生共有600人,则该年级参加足球活动的人数约人;
(3)、该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
23. 如图,将 绕点 顺时针旋转 得到 ,点 恰好落在 的延长线上,连接 . 分别交 于点 交 于点 . (1)、求 的角度;(2)、求证: .24. 佩佩宾馆重新装修后,有50间房可供游客居住,经市场调查发现,每间房每天的定价为140元,房间会全部住满,当每间房每天的定价每增加10元时,就会有一间房空闲,如果游客居住房间,宾馆需对每间房每天支出40元的各项费用.设每间房每天的定价增加 元,宾馆获利为 元.(1)、求 与 的函数关系式(不用写出自变量的取值范围) ;(2)、物价部门规定,春节期间客房定价不能高于平时定价的2倍,此时每间房价为多少元时宾馆可获利8000元?25. 如图,在 中, , 在 ,上取一点 ,以 为直径作 ,与 相交于点 ,作线段 的垂直平分线 交 于点 ,连接 .
(1)、求 的角度;(2)、求证: .24. 佩佩宾馆重新装修后,有50间房可供游客居住,经市场调查发现,每间房每天的定价为140元,房间会全部住满,当每间房每天的定价每增加10元时,就会有一间房空闲,如果游客居住房间,宾馆需对每间房每天支出40元的各项费用.设每间房每天的定价增加 元,宾馆获利为 元.(1)、求 与 的函数关系式(不用写出自变量的取值范围) ;(2)、物价部门规定,春节期间客房定价不能高于平时定价的2倍,此时每间房价为多少元时宾馆可获利8000元?25. 如图,在 中, , 在 ,上取一点 ,以 为直径作 ,与 相交于点 ,作线段 的垂直平分线 交 于点 ,连接 .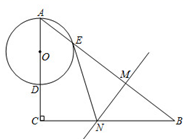 (1)、求证: 是 的切线;(2)、若 , 的半径为 .求线段 与线段 的长.26. 如图所示,在平面直角坐标系中,抛物线 的顶点坐标为 ,并与 轴交于点 ,点 是对称轴与 轴的交点.
(1)、求证: 是 的切线;(2)、若 , 的半径为 .求线段 与线段 的长.26. 如图所示,在平面直角坐标系中,抛物线 的顶点坐标为 ,并与 轴交于点 ,点 是对称轴与 轴的交点.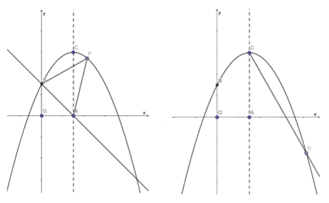 (1)、求抛物线的解析式;(2)、如图①所示, 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求 的面积的最大值;(3)、如图②所示,在对称轴 的右侧作 交抛物线于点 ,求出 点的坐标;并探究:在 轴上是否存在点 ,使 ?若存在,求点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图①所示, 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求 的面积的最大值;(3)、如图②所示,在对称轴 的右侧作 交抛物线于点 ,求出 点的坐标;并探究:在 轴上是否存在点 ,使 ?若存在,求点 的坐标;若不存在,请说明理由.