广西壮族自治区河池市凤山县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-26 类型:期末考试
一、单选题
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 将函数 的图象向右平移 个单位,再向下平移 个单位,可得到的抛物线是( )A、 B、 C、 D、4. 随机掷一枚均匀的硬币两次,落地后至少有一次正面朝上的概率是( )A、 B、 C、 D、15. 如图,将 (其中∠B=33°,∠C=90°)绕点 按顺时针方向旋转到 的位置,使得点C、A、B1在同一条直线上,那么旋转角等( )
2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 将函数 的图象向右平移 个单位,再向下平移 个单位,可得到的抛物线是( )A、 B、 C、 D、4. 随机掷一枚均匀的硬币两次,落地后至少有一次正面朝上的概率是( )A、 B、 C、 D、15. 如图,将 (其中∠B=33°,∠C=90°)绕点 按顺时针方向旋转到 的位置,使得点C、A、B1在同一条直线上,那么旋转角等( ) A、 B、 C、 D、6. 一条排水管的截面如图所示,已知排水管的半径 ,水面宽 ,则截面圆心 到水面的距离 是( )
A、 B、 C、 D、6. 一条排水管的截面如图所示,已知排水管的半径 ,水面宽 ,则截面圆心 到水面的距离 是( ) A、2 B、3 C、 D、2.57. 若关于 的一元二次方程 有两个实数根则 的取值范围是( )A、 B、 且 C、 且 D、8. 一个半径为2cm的圆的内接正六边形的面积是( )A、24cm2 B、6cm2 C、12cm2 D、8cm29. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=55°,则∠BCD的度数为( )
A、2 B、3 C、 D、2.57. 若关于 的一元二次方程 有两个实数根则 的取值范围是( )A、 B、 且 C、 且 D、8. 一个半径为2cm的圆的内接正六边形的面积是( )A、24cm2 B、6cm2 C、12cm2 D、8cm29. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=55°,则∠BCD的度数为( )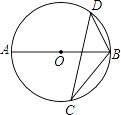 A、35° B、45° C、55° D、75°10. 函数 的图象上有两点 , ,若 ,则( )A、 B、 C、 D、 、 的大小不确定11. 三角形两边长分别是 和 ,第三边长是一元二次方程 的一个实数根,则该三角形的面积是( )A、 B、 C、 或 D、 或12. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、35° B、45° C、55° D、75°10. 函数 的图象上有两点 , ,若 ,则( )A、 B、 C、 D、 、 的大小不确定11. 三角形两边长分别是 和 ,第三边长是一元二次方程 的一个实数根,则该三角形的面积是( )A、 B、 C、 或 D、 或12. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、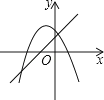 B、
B、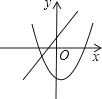 C、
C、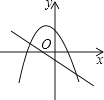 D、
D、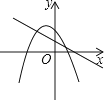
二、填空题
-
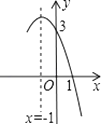
13. 在平面直角坐标系中,点(﹣2,3)关于原点对称的点的坐标是 .14. 从 这九个自然数中,任取一个数是偶数的概率是.15. 抛物线 的顶点坐标是.16. 设 分别为一元二次方程 的两个实数根,则 .17. 抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .
 18. 如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径 长为 ,母线 长为 .在母线 上的点 处有一块爆米花残渣,且 ,一只蚂蚁从杯口的点 处沿圆锥表面爬行到 点,则此蚂蚁爬行的最短距离为 .
18. 如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径 长为 ,母线 长为 .在母线 上的点 处有一块爆米花残渣,且 ,一只蚂蚁从杯口的点 处沿圆锥表面爬行到 点,则此蚂蚁爬行的最短距离为 .
三、解答题
-
19. 解下列方程:20. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).

( 1 )请画出 关于原点对称的 ;
( 2 )在 轴上求作一点 ,使 的周长最小,请画出 ,并直接写出 的坐标.
21. 某校九年级举行毕业典礼,需要从九年级(1)班的2名男生1名女生中和九年级(2)班的1名男生1名女生中各随机选出1名主持人.(1)、用树状图或列表法列出所有可能情形;(2)、求2名主持人恰好1男1女的概率.22. 已知关于x的一元二次方程x2+2x+m=0.(1)、当m=3时,判断方程的根的情况;(2)、当m=﹣3时,求方程的根.23. 我县寿源壹号楼盘准备以每平方米 元均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望,房地产开发商为了加快资金周转,对价格进行两次下调后,决定以每平方米 元的均价开盘销售.(1)、求平均每次下调的百分率.(2)、某人准备以开盘均价购买一套 平方米的住房,开发商给予以下两种优惠方案供选择:①打 折销售;
②不打折,一次性送装修费每平方米 元.
试问哪种方案更优惠?
24. 某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元.市场调査发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.(1)、求平均每天销售量 (箱)与销售价 (元/箱)之间的函数关系式.(2)、求该批发商平均每天的销售利润 (元)与销售价 (元/箱)之间的函数关系式.(3)、当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?25. 如图,在 中, , 的平分线交 于 , 为 上一点, ,以 为圆心,以 的长为半径画圆. (1)、求证: 是⊙ 的切线;(2)、求证: .26. 如图,已知抛物线经过坐标原点 和 轴上另一点 ,顶点 的坐标为 .矩形 的顶点 与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)、求证: 是⊙ 的切线;(2)、求证: .26. 如图,已知抛物线经过坐标原点 和 轴上另一点 ,顶点 的坐标为 .矩形 的顶点 与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.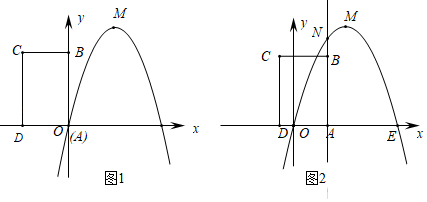 (1)、求该抛物线所对应的函数关系式;(2)、将矩形 以每秒 个单位长度的速度从图1所示的位置沿 轴的正方向匀速平行移动,同时一动点 也以相同的速度从点 出发向 匀速移动,设它们运动的时间为 秒 ,直线 与该抛物线的交点为 (如图2所示).
(1)、求该抛物线所对应的函数关系式;(2)、将矩形 以每秒 个单位长度的速度从图1所示的位置沿 轴的正方向匀速平行移动,同时一动点 也以相同的速度从点 出发向 匀速移动,设它们运动的时间为 秒 ,直线 与该抛物线的交点为 (如图2所示).①当 ,判断点 是否在直线 上,并说明理由;
②设P、N、C、D以为顶点的多边形面积为 ,试问 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.