广西壮族自治区北海市2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-11-26 类型：期末考试

进入出卷网下载

一、单选题

1. sin30°等于（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
2. 下列方程中，是关于x的一元二次方程的是（）

A、5x+5＝2x﹣1 B、y²﹣7y＝0 C、ax²+bc+c＝0 D、2x²+2x＝x²-1

查看试题解析
3. 如图，在Rt△ABC中，∠C=90°，AC=3，AB=5，则cosB的值为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、 $\frac{3}{5}$

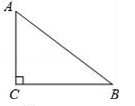查看试题解析
4. 随机抽取某商场4月份5天的营业额（单位：万元）分别为3.4，2.9，3.0，3.1，2.6，则这个商场4月份的营业额大约是（）

A、90万元 B、450万元 C、3万元 D、15万元

查看试题解析
5. 用配方法解方程 $x^{2} - 2 x - 1 = 0$ 时，配方后所得的方程为（）

A、 $（ x + 1 ）^{2} = 0$ B、 $（ x - 1 ）^{2} = 0$ C、 $（ x + 1 ）^{2} = 2$ D、 $（ x - 1 ）^{2} = 2$

查看试题解析
6. 如图，在△ABC中，DE∥BC， $\frac{A D}{B D}$ ＝ $\frac{1}{2}$ ，DE＝4cm，则BC的长为（）

A、8cm B、12cm C、11cm D、10cm

查看试题解析
7. 某闭合电路中，电源的电压为定值，电流I（A）与电阻R（Ω）成反比例.图表示的是该电路中电流I与电阻R之间函数关系的图象，则用电阻R表示电流I的函数解析式为（）

A、 $I= \frac{2}{R}$ B、 $I= \frac{3}{R}$ C、 $I= \frac{6}{R}$ D、 $I= - \frac{6}{R}$

查看试题解析
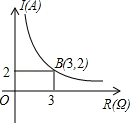8. 方程x²+4x+4＝0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、没有实数根

查看试题解析
9.
如图，铁道口的栏杆短臂长1m，长臂长16m．当短臂端点下降0.5m时，长臂端点升高（　　）

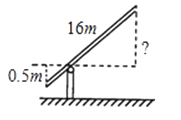A、5m B、6m C、7m D、8m

查看试题解析
10. 有x支球队参加篮球比赛，每两队之间都比赛一场，共比赛了21场，则下列方程中符合题意的是（）

A、x（x﹣1）＝21 B、x（x﹣1）＝42 C、x（x+1）＝21 D、x（x+1）＝42

查看试题解析
11. 有一副三角板，含45°的三角板的斜边与含30°的三角板的长直角边相等，如图，将这副三角板直角顶点重合拼放在一起，点B，C，E在同一直线上，若BC＝2，则AF的长为（）

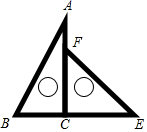A、2 B、2 $\sqrt{3}$ ﹣2 C、4﹣2 $\sqrt{3}$ D、2 $\sqrt{3}$ ﹣ $\sqrt{6}$

查看试题解析
12. 如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于A，B，与反比例函数 $y = \frac{k}{x}$ （k＞0）在第一象限的图象交于点E，F，过点E作EM⊥y轴于M，过点F作FN⊥x轴于N，直线EM与FN交于点C，若 $\frac{B E}{B F} = \frac{1}{3}$ ，则△OEF与△CEF的面积之比是（）

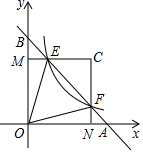A、2：1 B、3：1 C、2：3 D、3：2

查看试题解析

二、填空题

13. 一元二次方程x²=4的解是．

查看试题解析
14. 如果 $\frac{a}{b} = \frac{3}{2}$ ，那么 $\frac{a + b}{b}$ = ．

查看试题解析
15. 为了估计虾塘里海虾的数目，第一次捕捞了500只虾，将这些虾一一做上标记后放回虾塘.几天后，第二次捕捞了2000只虾，发现其中有20只虾身上有标记，则可估计该虾塘里约有只虾.

查看试题解析
16. 计算：2 $\sqrt{3}$ cos30°+tan45°﹣4sin²60°＝.

查看试题解析
17. 如图，在平面直角坐标系xOy中，已知点A（3，3）和点B（7，0），则tan∠ABO＝.

查看试题解析
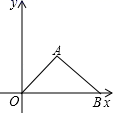18. 如图，已知点A、B分别在反比例函数y＝ $\frac{1}{x}$ （x＞0），y＝﹣ $\frac{5}{x}$ （x＞0）的图象上，且OA⊥OB，则 $\frac{O B}{O A}$ 的值为.

查看试题解析

三、解答题

19. 利用公式法解方程：x²﹣x﹣3＝0.

查看试题解析
20. 如图，A，B，C三点的坐标分别为A(1，0)，B(4，3)，C(5，0)，试在原图上画出以点A为位似中心，把△ABC各边长缩小为原来的一半的图形，并写出各顶点的坐标.

查看试题解析
21. 如图，等边三角形ABC放置在平面直角坐标系中，已知A（0，0），B（4，0），反比例函数的图象经过点C.求点C的坐标及反比例函数的解析式.

查看试题解析
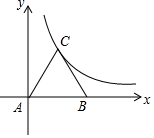22. 测量计算是日常生活中常见的问题，如图，建筑物BC的屋顶有一根旗杆AB，从地面上D点处观测旗杆顶点A的仰角为50°，观测旗杆底部B点的仰角为45°(参考数据：sin50°≈0.8，tan50°≈1.2).

(1)、若已知CD＝20米，求建筑物BC的高度；

(2)、若已知旗杆的高度AB＝5米，求建筑物BC的高度.

查看试题解析
23. 2019年全国青少年禁毒知识竞赛开始以来，某市青少年学生踊跃参加，掀起了学习禁毒知识的热潮，禁毒知识竞赛的成绩分为四个等级：优秀，良好，及格，不及格.为了了解该市广大学生参加禁毒知识竞赛的成绩，抽取了部分学生的成绩，根据抽查结果，绘制了如下两幅不完整的统计图：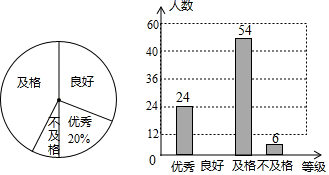

(1)、本次抽查的人数是；扇形统计图中不及格学生所占的圆心角的度数为；

(2)、补全条形统计图；

(3)、若某校有2000名学生，请你根据调查结果估计该校学生知识竞赛成绩为“优秀”和“良好”两个等级共有多少人？

查看试题解析
24. 如图，已知一次函数y＝x﹣2与反比例函数y＝ $\frac{3}{x}$ 的图象交于A、B两点.

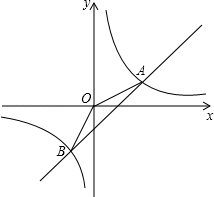(1)、求A、B两点的坐标；

(2)、求△AOB的面积.

查看试题解析
25. 随着人民生活水平的不断提高，某市家庭轿车的拥有量逐年增加，据统计，该市2017年底拥有家庭轿车64万辆，2019年底家庭轿车的拥有量达到100万辆.

(1)、求2017年底至2019年底该市汽车拥有量的年平均增长率；

(2)、该市交通部门为控制汽车拥有量的增长速度，要求到2020年底全市汽车拥有量不超过118万辆，预计2020年报废的汽车数量是2019年底汽车拥有量的8%，求2019年底至2020年底该市汽车拥有量的年增长率要控制在什么范围才能达到要求.

查看试题解析
26. 已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），tan∠BAC＝ $\frac{3}{4}$ .

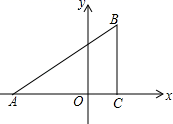(1)、写出点B的坐标；

(2)、在x轴上找一点D，连接BD，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；

(3)、在（2）的条件下，如果点P从点A出发，以2cm/秒的速度沿AB向点B运动，同时点Q从点D出发，以1cm/秒的速度沿DA向点A运动.当一个点停止运动时，另一个点也随之停止运动.设运动时间为t.问是否存在这样的t使得△APQ与△ADB相似？如存在，请求出t的值；如不存在，请说明理由.

查看试题解析