广西贺州市平桂区2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-11-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次函数的开口方向一定向上的是（）

A、 $y = - 3 x^{2}$ B、 $y = a x^{2}$ C、 $y = 3 x^{2}$ D、 $y = (a - 1) x^{2}$

查看试题解析
2. 若 $\frac{a - b}{b} = \frac{3}{4}$ ，则 $\frac{a}{b}$ 的值是（）

A、 $\frac{4}{3}$ B、 $\frac{7}{3}$ C、 $\frac{4}{7}$ D、 $\frac{7}{4}$

查看试题解析
3. 两个相似三角形对应高之比为 $1 : 2$ ，那么它们的对应中线之比为（）

A、 $1 : 2$ B、 $1 : 3$ C、 $1 : 4$ D、 $1 : 8$

查看试题解析
4. 过反比例函数 $y = - \frac{6}{x}$ 图象上一点作两坐标轴的垂线段，则它们与两坐标轴围成的四边形面积为（）

A、－6 B、－3 C、3 D、6

查看试题解析
5. 在Rt△ABC中，∠C＝90°，若 $\cos B = \frac{1}{2}$ ，则 $\sin A$ 的值为（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
6. 关于二次函数 $y = 2 x^{2} + 4$ ，下列说法错误的是（）

A、它的图象开口方向向上 B、它的图象顶点坐标为（0，4） C、它的图象对称轴是y轴 D、当 $x = 0$ 时，y有最大值4

查看试题解析
7. 如图，△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC的面积比是4：9，则OB′：OB为（）

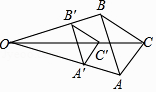A、2：3 B、3：2 C、4：5 D、4：9

查看试题解析
8. 某同学推铅球，铅球出手高度是 $\frac{5}{3}$ m，出手后铅球运行高度y（m）与水平距离x（m）之间的函数表达式为 $y = a {(x - 4)}^{2} + 3$ ，则该同学推铅球的成绩为（）

A、9m B、10m C、11m D、12m

查看试题解析
9. 如图，学校的保管室有一架5m长的梯子斜靠在墙上，此时梯子与地面所成的角为45°如果梯子底端O固定不变，顶端靠到对面墙上，此时梯子与地面所成的角为60°，则此保管室的宽度AB为（）

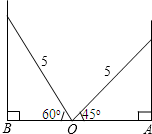A、 $\frac{5}{2}$ ( $\sqrt{2}$ +1 ) m B、 $\frac{5}{2}$ ( $\sqrt{2}$ +3 ) m C、( $3 + \sqrt{2}$ ) m D、 $\frac{5}{2}$ ( $\sqrt{3}$ +1 ) m

查看试题解析
10. 已知二次函数 $y = (k - 2) x^{2} + 2 x + 1$ 的图象与x轴只有一个交点，则这个交点的坐标为（）

A、（0，－1） B、（0，1） C、（－1，0） D、（1，0）

查看试题解析
11. 如图，一斜坡AB的长为 $2 \sqrt{13}$ m，坡度为1：1.5，则该斜坡的铅直高度BC的高为（）

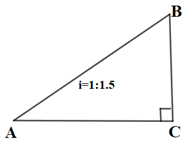A、3m B、4m C、6m D、16m

查看试题解析
12. 如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则sin∠BDE的值是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{\sqrt{2}}{4}$

查看试题解析

二、填空题

13. 计算： $\sqrt{2}$ sin45°＝.

查看试题解析
14. 抛物线 $y = {(x - 2)}^{2}$ 的顶点坐标是.

查看试题解析
15. 点A $(- 2, y_{1})$ ，B $(- 1, y_{2})$ 都在反比例函数 $y = - \frac{3}{x}$ 图象上，则 $y_{1}$ $y_{2}$ .（填写<，>，=号）

查看试题解析
16. 如图，在△ABC中，点D，E分别是AC，BC边上的中点，则△DEC的周长与△ABC的周长比等于.

查看试题解析
17. 如图，在Rt△ABC中，∠C=90°，点D为BC上一点，AD=BD，CD=1，AC= $\sqrt{3}$ ，则∠B的度数为 .

查看试题解析
18. 如图，四边形ABCD中，AB∥CD，∠C＝90°，AB＝1，CD＝2，BC＝3，点P为BC边上一动点，若AP⊥DP，则BP的长为.

查看试题解析

三、解答题

19. 计算： ${(\frac{1}{2})}^{- 1} - 2 \cos 30 ° - {(2019 + π)}^{0} + 2 \sqrt{3} \sin 30 °$ .

查看试题解析
20. 已知反比例函数 $y = \frac{m - 5}{x}$ 的图象过点P（－1，3），求m的值和该反比例函数的表达式.

查看试题解析
21. 如图，在锐角三角形ABC中，AB=4，BC= $3 \sqrt{3}$ ，∠B=60°，求△ABC的面积

查看试题解析
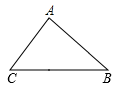22. 如图，在△ABC中，D为BC边上的一点，且AC= $2 \sqrt{6}$ ，CD＝4，BD＝2，求证：△ACD∽△BCA.

查看试题解析
23. 已知抛物线 $y = 2 x^{2} - 12 x + 13$ .

(1)、当x为何值时，y随x的增大而减小；

(2)、将该抛物线向右平移2个单位，再向上平移2个单位，请直接写出平移后的抛物线表达式.

查看试题解析
24. 如图，在▱ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE= $\frac{1}{2}$ CD

(1)、求证：△ABF∽△CEB

(2)、若△DEF的面积为2，求△CEB的面积

查看试题解析
25. 某校有一露天舞台，纵断面如图所示，AC垂直于地面，AB表示楼梯，AE为舞台面，楼梯的坡角∠ABC=45°，坡长AB=2m，为保障安全，学校决定对该楼梯进行改造，降低坡度，拟修新楼梯AD，使∠ADC=30°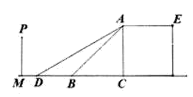

(1)、求舞台的高AC(结果保留根号)

(2)、楼梯口B左侧正前方距离舞台底部C点3m处的文化墙PM是否要拆除?请说明理由.

查看试题解析
26. 如图，已知抛物线 $y = - x^{2} + m x + n$ 与x轴交于A、B两点，与y轴交于C点，其中A(1，0)，C(0，3).

(1)、求该抛物线的解析式；

(2)、求该抛物线的对称轴及点B的坐标；

(3)、设点P为该抛物线对称轴上的一个动点，是否存在点P使△BPC为直角三角形，若存在，求出点P的坐标；若不存在，请说明理由.

查看试题解析