广西百色市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-11-26 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
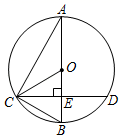
D、 2. 二次函数 的最小值是 ( )A、 2 B、2 C、 1 D、13. 如图,点 , , 都在 上,若 ,则 为( )
2. 二次函数 的最小值是 ( )A、 2 B、2 C、 1 D、13. 如图,点 , , 都在 上,若 ,则 为( ) A、34° B、56° C、60° D、68°4. 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=6,DB=3,则 的值为( )
A、34° B、56° C、60° D、68°4. 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=6,DB=3,则 的值为( )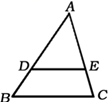 A、 B、 C、 D、25. 某水库大坝的横断面是梯形,坝内一斜坡的坡度 ,则这个斜坡坡角为( )A、30° B、45° C、60° D、90°6. 如图,在高2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
A、 B、 C、 D、25. 某水库大坝的横断面是梯形,坝内一斜坡的坡度 ,则这个斜坡坡角为( )A、30° B、45° C、60° D、90°6. 如图,在高2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( ) A、2 m B、(2+ 2 )m C、4 m D、(4+ 2 )m7. 如图平行四边变形ABCD中,E是BC上一点,BE∶EC=2∶3,AE交BD于F,则S△BFE∶S△FDA等于( )
A、2 m B、(2+ 2 )m C、4 m D、(4+ 2 )m7. 如图平行四边变形ABCD中,E是BC上一点,BE∶EC=2∶3,AE交BD于F,则S△BFE∶S△FDA等于( )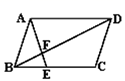 A、2∶5 B、4∶9 C、4∶25 D、2∶38. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、9. 如图,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 取值范围是( )
A、2∶5 B、4∶9 C、4∶25 D、2∶38. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、9. 如图,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 取值范围是( )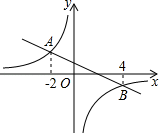 A、 或 B、 或 C、 或 D、 或10. 如图,AB是⊙O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△BDA相似,可以添加一个条件.下列添加的条件中错误的是( )
A、 或 B、 或 C、 或 D、 或10. 如图,AB是⊙O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△BDA相似,可以添加一个条件.下列添加的条件中错误的是( )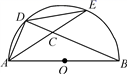 A、∠ACD=∠DAB B、AD=DE C、AD·AB=CD·BD D、AD2=BD·CD11. 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A、∠ACD=∠DAB B、AD=DE C、AD·AB=CD·BD D、AD2=BD·CD11. 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( ) A、 B、2 C、 D、12. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1﹣k2=( ).
A、 B、2 C、 D、12. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1﹣k2=( ).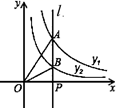 A、-2 B、2 C、-4 D、4
A、-2 B、2 C、-4 D、4二、填空题
-
13. 如图,请补充一个条件:,使△ACB∽△ADE.
 14. 如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC= .
14. 如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC= .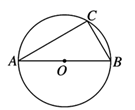 15. 在Rt△ABC中, , , ,则 的值等于 .16. 如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,在点O的异侧将△OAB缩小为原来的 ,则点B的对应点的坐标是.
15. 在Rt△ABC中, , , ,则 的值等于 .16. 如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,在点O的异侧将△OAB缩小为原来的 ,则点B的对应点的坐标是. 17. 如图,A、B两点在双曲线y= 上,分别经过A、B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2= .
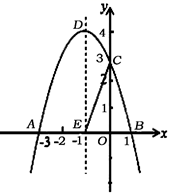
17. 如图,A、B两点在双曲线y= 上,分别经过A、B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2= .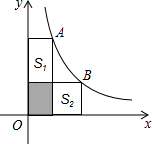 18. 已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x轴、y轴的交点分别为A,B,点P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0;②x=3是ax2+bx+3=0的一个根;③△PAB周长的最小值是 +3 .其中正确的是.
18. 已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x轴、y轴的交点分别为A,B,点P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0;②x=3是ax2+bx+3=0的一个根;③△PAB周长的最小值是 +3 .其中正确的是.
三、解答题
-
19. 计算:2cos45° tan30°cos30°+sin260°.20. 如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣1,1)、B(0,﹣2)、C(1,0),点P(0,2)绕点A旋转180°得到点P1 , 点P1绕点B旋转180°得到点P2 , 点P2绕点C旋转180°得到点P3 ,
 (1)、在图中画出点P1、P2、P3;(2)、继续将点P3绕点A旋转180°得到点P4 , 点P4绕点B旋转180°得到点P5 , …,按此作法进行下去,则点P2020的坐标为 .21. 在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AD=8,DB=2,求CD的长
(1)、在图中画出点P1、P2、P3;(2)、继续将点P3绕点A旋转180°得到点P4 , 点P4绕点B旋转180°得到点P5 , …,按此作法进行下去,则点P2020的坐标为 .21. 在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AD=8,DB=2,求CD的长 22. 如图,已如平行四边形OABC中,点O为坐标顶点,点A(3,0),B(4,2),函数 (k≠0)的图象经过点C.
22. 如图,已如平行四边形OABC中,点O为坐标顶点,点A(3,0),B(4,2),函数 (k≠0)的图象经过点C.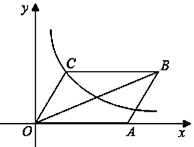 (1)、求反比例的函数表达式:(2)、请判断平行四边形OABC对角线的交点是否在函数 (k≠0)的图象上.23. 如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度.
(1)、求反比例的函数表达式:(2)、请判断平行四边形OABC对角线的交点是否在函数 (k≠0)的图象上.23. 如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度.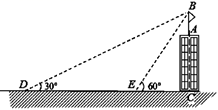 24. 某大型商场出售一种时令鞋,每双进价100元,售价300元,则每天能售出400双.经市场调查发现:每降价10元,则每天可多售出50双.设每双降价x元,每天总获利y元.(1)、如果降价40元,每天总获利多少元呢?(2)、每双售价为多少元时,每天的总获利最大?最大获利是多少?
24. 某大型商场出售一种时令鞋,每双进价100元,售价300元,则每天能售出400双.经市场调查发现:每降价10元,则每天可多售出50双.设每双降价x元,每天总获利y元.(1)、如果降价40元,每天总获利多少元呢?(2)、每双售价为多少元时,每天的总获利最大?最大获利是多少?