江苏省扬州市江都区八校2020-2021学年七年级上学期数学10月月考试卷

试卷更新日期：2020-11-26 类型：月考试卷

进入出卷网下载

一、单选题

1. $- \frac{1}{3}$ 的相反数是（）

A、3 B、-3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 若数轴上表示﹣1和3的两点分别是点A和点B，则点A和点B之间的距离是（）

A、﹣4 B、﹣2 C、2 D、4

查看试题解析
3. 下列各式中正确的是（）

A、 $| 5 | = 5$ B、 $- | - 5 | = | - 5 |$ C、 $| - 5 | = - 5$ D、 $| - 5 | < 0$

查看试题解析
4. 下列说法中正确的是（）

A、有理数就是有限小数和无限小数的统称 B、数轴上的点表示的数都是有理数 C、一个有理数不是整数就是分数 D、正分数、零、负分数统称为分数

查看试题解析
5. 计算 $(- 2) - 5$ 的结果等于（）

A、 $- 7$ B、-3 C、3 D、7

查看试题解析
6. 已知a、b两数在数轴上对应的点如图所示，下列结论正确的是（）

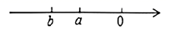A、ab<0 B、│a│>│b│ C、a+b>0 D、b－a<0

查看试题解析
7. 已知： $| x |$ =3， $| y |$ =2，且x＞y ，则x+y的值为（）

A、5 B、1 C、5或1 D、－5或－1

查看试题解析
8. 观察下列算式， $2^{1} = 2$ ， $2^{2} = 4$ ， $2^{3} = 8$ ， $2^{4} = 16$ ， $2^{5} = 32$ ， $2^{6} = 64$ ， $2^{7} = 128$ ， $2^{8} = 256$ ，用你所发现的规律得出 $2^{2020}$ 的末位数字是（）

A、2 B、4 C、6 D、8

查看试题解析

二、填空题

9. 如果+20表示向南走20m ，那么向北走60m表示为．

查看试题解析
10. 据统计，全国每小时约有510000000吨污水排入江海，用科学记数法表示为．

查看试题解析
11. 把 $(- 5) - (+ 3) + (- 2) - (- 1)$ 写成省略括号的和形式．

查看试题解析
12. 如果a是最大的负整数，b是最小的正整数，那么 $a - b$ 的值为．

查看试题解析
13. 数轴上离表示 $- 2$ 的点距离等于3个单位长度的点表示的数是.

查看试题解析
14. 用“ $< ”$ 或“ $> ”$ 填空： $- | - 3 |$ $- (- 3.1)$ ．

查看试题解析
15. 池塘里浮萍面积每天长大一倍,若经过12天长满整个池塘,问需天浮萍长满半个池塘；

查看试题解析
16. $| x - 3 | + {(y + 2)}^{2} = 0$ ，则 $y^{x}$ 为．

查看试题解析
17. 如图是一个计算程序，当输出值y＝16时，输入值x为．

查看试题解析
18. 如图1，圆的周长为4个单位，在该圆的4等分点处分别标上字母m、n、p、q ，如图2，先让圆周上表示m的点与数轴原点重合，再将数轴按逆时针方向环绕在该圆上，则数轴上表示﹣2018的点与圆周上重合的点对应的字母是．

查看试题解析

三、解答题

19. 把下列各数填入表示它所在的数集的括号里．
$- (- 2.3)$ ， $\frac{22}{7}$ ， 0 ， $- 2^{4}$ ， $30 %$ ，π ， $- | - 2013 |$ ， $- 5 \frac{1}{2}$   ， $0. \overset{\cdot}{3}$

负整数集合{               }

正有理数集合{           }

分数集合{                  }．

查看试题解析
20. 计算题

(1)、 $12 - 18 + 7 - 15$ ；

(2)、 $\frac{3}{4} \times (- 7) - (- 13) \times (- \frac{3}{4})$ ；

(3)、 $(- \frac{1}{2} - \frac{1}{3} + \frac{3}{4}) \times (- 60)$ ；

(4)、-1²- $\frac{1}{6}$ ×[（-2）³+（-3）²]；

查看试题解析
21. 用数轴上的点表示下列各数，并用“<”将它们连起来：－5 $\frac{1}{2}$ ， $- | - 4 |$ ， 2， 0，－2 $\frac{1}{3}$

查看试题解析
22. 一只小虫从某点P出发，在一条直线上来回爬行，假定把向右爬行的路程记为正数，向左爬行的路程记为负数，则爬行各段路程 $($ 单位：厘米 $)$ 依次为：
+5，-4， $+ 10$ ，-8，-7，+14，-6

(1)、通过计算说明小虫是否回到起点P；

(2)、如果小虫爬行的速度为0.6厘米/秒，那么小虫共爬行了多长时间．

查看试题解析
23. 若a与b互为相反数，c与d互为倒数，m的绝对值为4，试求 $\frac{a + b}{m} + c d - m$ 的值；

查看试题解析
24. 已知a、b为有理数，现规定一种新运算，满足a*b=a $\times$ b－a+b

(1)、求2*4的值；

(2)、求（1*3）*（－2）的值．

查看试题解析
25. 某自行车厂计划平均每人每天生产30辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况 $($ 超产为正、减产为负 $)$ ：

星期

一

二

三

四

五

增减

+8

+2

-4

+6

-2

(1)、根据记录可知前三天共生产辆；

(2)、产量最多的一天比产量最少的一天多生产辆；

(3)、该厂实行每周计件工资制，每生产一辆车可得15元，若超额完成任务，则超过部分每辆另奖10元；少生产一辆扣10元，那么该厂工人这一周 $(5$ 天 $)$ 的工资总额是多少？

查看试题解析
26. 已知在纸面上有一数轴 $($ 如图 $)$ ，折叠纸面：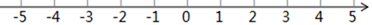

(1)、若1表示的点与-1表示的点重合，则 $- 2$ 表示的点与数表示的点重合；

(2)、若-1表示的点与5表示的点重合，回答以下问题：
①6表示的点与数表示的点重合；

②若数轴上A、B两点之间的距离为 $11 (A$ 在B的左侧 $)$ ，且A、B两点经折叠后重合，求A、B两点表示的数是多少？

查看试题解析
27. 如图，一只甲虫在5×5的方格 $($ 每小格边长为 $1)$ 上沿着网格线运动．它从A处出发去看望B、C、D处的其他甲虫．规定：向上、向右走为正，向下、向左走为负．如从A到B记为： $A \to B$ （+1，+4），从B到A记为： $A \to B$ （-1，-4），括号内第一个数表示左右方向，第二个数表示上下方向，那么图中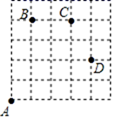

(1)、 $A \to C$ ( ， )， $B \to C$ （，）， $C \to$ $(+ 1 ， - 2)$ ，

(2)、若这只甲虫的行走路线为 $A \to B \to C \to D$ ，请计算该甲虫走过的）路程；

(3)、若这只甲虫从A处去甲虫P处的行走路线一次为 $(+ 2 ， + 2)$ ， $(+ 2 ， - 1)$ ， $(- 2 ， + 3)$ ， $(- 1 ， - 2)$ ，请在图中标出P的位置．

查看试题解析
28. 如图在数轴上 $A$ 点表示数 $a$ ， $B$ 点表示数 $b$ 、 $a$ 、 $b$ 满足 $| a + 2 | + | b - 4 | = 0$ ；

(1)、点 $A$ 表示的数为；点 $B$ 表示的数为；

(2)、若在原点 $O$ 处放一挡板．一小球甲从点 $A$ 处以1个单位/秒的速度向左运动：同时另小球乙从点 $B$ 处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为 $t$ （秒）．
①当 $t = 1$ 时，甲小球到原点的距离＝；乙小球到原点的距离＝．

当 $t = 3$ 时，甲小球到原点的距离=；乙小球到原点的距离= ．

②试探究：甲、乙两小球到原点的距离可能相等吗？若不能，请说明理由，若能，请直接写出甲，乙两小球到原点的距离相等时经历的时间．

查看试题解析

星期	一	二	三	四	五
增减	+8	+2	-4	+6	-2