江苏省江阴市青阳片2020-2021学年七年级上学期数学10月月考试卷

试卷更新日期：2020-11-26 类型：月考试卷

进入出卷网下载

一、单选题

1. -2的相反数等于（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、-2 D、2

查看试题解析
2. 在下列各数－（＋5）、－1、+（－ $\frac{1}{3}$ ）、－（－1）、－|－3|中，负数有（）

A、2个 B、3个 C、4 个 D、5个

查看试题解析
3. 下面各组数中，相等的一组是（）

A、－2²与（－2）² B、 $\frac{2^{3}}{3}$ 与 ${(\frac{2}{3})}^{3}$ C、 $- | - 2 |$ 与－（－2） D、（－3）³与－3³

查看试题解析
4. 冬季某天我国三个城市的最高气温分别是－13℃，1℃，－3℃，它们任意两城市中最大的温差是（）

A、12℃ B、16℃ C、10℃ D、14℃

查看试题解析
5. 写成省略加号和的形式后为－6－8－2＋4的式子是（）

A、（－6）－（＋8）－（－2）＋（＋4） B、－（＋6）－（－8）－（＋2）－（＋4） C、（－6）＋（－8）＋（＋2）－（－4） D、－6－（＋8）＋（－2）－（－4）

查看试题解析
6. 马虎同学做了以下4道计算题：①0﹣（﹣1）=1；② $\frac{1}{2}$ ÷（﹣ $\frac{1}{2}$ ）=﹣1；③﹣ $\frac{5}{7}$ + $\frac{2}{7}$ =﹣（ $\frac{5}{7}$ + $\frac{2}{7}$ ）=﹣1；④﹣7﹣2×5=﹣9×5=﹣45.请你帮他检查一下，他一共做对了（）

A、1题 B、2题 C、3题 D、4题

查看试题解析
7. 下列说法中，正确的是（）

A、在数轴上表示 $- a$ 的点一定在原点的左边 B、有理数a的倒数是 $\frac{1}{a}$ C、一个数的相反数一定小于或等于这个数 D、如果一个数的绝对值等于这个数的相反数,那么这个数是负数或零

查看试题解析
8. 下列各组数中互为相反数的一组是（）

A、3与 $\frac{1}{3}$ B、2与 $| - 2 |$ C、 $- | - 1 |$ 与-1 D、－4与 ${(-2)}^{2}$

查看试题解析
9. 如图所示是计算机某计算程序，若开始输入x＝－2，则最后输出的结果是（）

A、－4 B、－10 C、－6 D、－12

查看试题解析
10. 如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下一次沿顺时针方向跳两个点；若停在偶数点上，则下一次沿逆时针方向跳一个点.若青蛙从数1这点开始跳，第1次跳到数3那个点，如此，则经2015次跳后它停的点所对应的数为（）

A、5 B、3 C、2 D、1

查看试题解析

二、填空题

11. 如果向西走5m，记作＋5m，那么－10m表示。

查看试题解析
12. 地球的表面积约是510 000 000km² ，可用科学记数法表示为km².

查看试题解析
13. 比较大小：（填“﹥”、“﹤”或“=”）

(1)、－|－2| $- (- 2)$ ；

(2)、 $- \frac{4}{5}$ $- \frac{3}{4}$

查看试题解析
14. 绝对值不大于3的所有整数有

查看试题解析
15. 已知|a|＝1，|b|＝5，且a＞b，则a－b的值＝.

查看试题解析
16. 若 $| x - 2 | + {(y + 3)}^{2} = 0$ ，则 $\sqrt{{(x + y)}^{2014}}$ ＝.

查看试题解析
17. 用形状和大小相同的黑色棋子按下图所示的方式排列，按照这样的规律，第101个图形需要棋子枚.

查看试题解析
18. 已知整数a₁ ， a₂ ， a₃ ， a₄ ， …满足下列条件：a₁=0，a₂= -|a₁+1|，a₃= -|a₂+2|，a₄= -|a₃+3|，…依次类推，则a₂₀₁₃的值为.

查看试题解析

三、解答题

19. 把下列各数填入表示它所在的数集的括号内：
－ $\frac{22}{7}$ ，π，－0.1010010001……，0，－（－2.28），－|－4|，－3²

正数集合｛                       …｝

分数集合｛                       …｝

整数集合｛                       …｝

无理数集合｛                     …｝

查看试题解析
20. 画出数轴，在数轴上标出表示下列各数的点，并按从大到小的顺序用“＞”号把这些数连接起来：－|－2.5|，0，－(－ $\frac{1}{2}$ )，＋(－1)²⁰¹⁵ ， $- 2^{2}$

查看试题解析
21. 计算

(1)、-20+（-5）-（-18）

(2)、 $(- 1 \frac{1}{2}) + 1.25 + (- 8.5) - (- 10 \frac{3}{4})$

(3)、 $- 81 \div \frac{9}{4} \times \frac{4}{9} \div (- 16)$

(4)、（－ $\frac{1}{3} - \frac{1}{6} + \frac{1}{8}$ ）×（-24）

查看试题解析
22. 规定☆是一种运算，并满足：a☆b＝a×b－a÷b，例如：5☆2＝5×2－5÷2，试计算：

(1)、8☆（－2）的值

(2)、比较大小8☆（－2）（－2） ☆8（填“﹥”、“﹤”或“=”）

查看试题解析

23. 某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入。下表是某周的生产情况（超产记为正、减产记为负）:

星期	一	二	三	四	五	六	日
增减	+5	－2	－4	＋12	－10	＋16	－9

(1)、根据记录的数据可知该厂星期六生产自行车辆；

(2)、根据记录的数据可知该厂本周实际生产自行车辆；

(3)、产量最多的一天比产量最少的一天多生产自行车辆；

(4)、该厂实行每周计件工资制，每生产一辆车可得50元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？

查看试题解析

24. 数学实验室：
点A、B在数轴上分别表示有理数a、b， A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a﹣b|.

利用数形结合思想回答下列问题：

(1)、数轴上表示2和5的两点之间的距离是，数轴上表示1和－3的两点之间的距离是；

(2)、数轴上若点A表示的数是x，点B表示的数是－2，则点A和B之间的距离是，若AB＝2，那么x为；

(3)、当x是时，代数式 $| x + 2 | + | x - 1 | = 5$ ；

(4)、若点A表示的数－1，点B与点A的距离是10，且点B在点A的右侧，动点P、Q同时从A、B出发沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒1个单位长度，则运动秒后，PQ=1？

查看试题解析
25. 阅读理解：
若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是（A，B）的好点.

例如，如图1，点A表示的数为－1，点B表示的数为2.表示1的点C到点A的距离是2，到点B的距离是1，那么点C是（A，B）的好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是（A，B）的好点，但点D是（B，A）的好点.

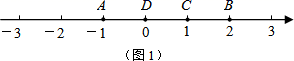
知识运用：

(1)、如图2，M、N为数轴上两点，点M所表示的数为－2，点N所表示的数为4.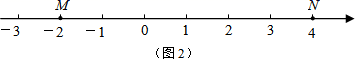

在点M和点N中间，数所表示的点是（M，N）的好点；

(2)、在数轴上，数和数所表示的点都是（N，M）的好点；

(3)、如图3，A、B为数轴上两点，点A所表示的数为－20，点B所表示的数为40.现有一只电子蚂蚁P从点B出发，以2个单位每秒的速度向左运动，到达点A停止.当t为何值时，P、A和B中恰有一个点为其余两点的好点？

查看试题解析