江苏省无锡市羊尖中2020-2021学年八年级上学期数学9月月考试卷

试卷更新日期：2020-11-26 类型：月考试卷

进入 出卷网 下载

一、单选题

  • 1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 一个等腰三角形的两边长分别是3和7，则它的周长为（  ）
    A、17 B、15 C、13 D、13或17

    查看试题解析

  • 3. 下列能判定△ABC为等腰三角形的是（   ）
    A、∠A=50°，∠B=40° B、∠A=70°，∠B=40° C、AB=AC=4，BC=8 D、AB=3，BC=8，周长为16

    查看试题解析

  • 4. 如图，已知AB=AC，AD=AE，若要得到△ABD≌△ACE，必须添加一个条件，则下列所添条件不恰当的是 （ ）．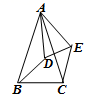

    A、BD=CE B、∠ABD=∠ACE C、∠BAD=∠CAE D、∠BAC=∠DAE

    查看试题解析

  • 5. 下列说法中正确的是（   ）
    A、10的平方根是100 B、－2不是4的平方根 C、49 的平方根是 23 D、0.01的算术平方根是0.1

    查看试题解析

  • 6. 如果y= x−4 + 4−x +1，则2x+y的平方根是（   ）
    A、9 B、±9 C、3 D、±3

    查看试题解析

  • 7. 如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为（   ）

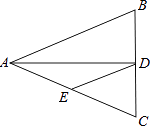    A、20 B、12 C、14 D、13

    查看试题解析

  • 8. 如图，正方形网格中，网格线的交点称为格点，已知A，B是两格点，如果C也是图中的格点，且使得 △ABC 为等腰三角形，则点C的个数有 (    )

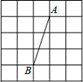    A、4个 B、6个 C、8个 D、10个

    查看试题解析

  • 9. 到三角形三个顶点距离相等的点是（   ）
    A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点

    查看试题解析

  • 10. 如图的2×4的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形，在网格中与△ABC成轴对称的格点三角形一共有（   ）

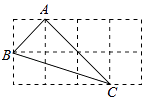    A、2个 B、3个 C、4个 D、5个

    查看试题解析

二、填空题

  • 11. 若x2＝3，则x＝；若 x ＝3，则x＝；若 x+(y−1)2 ＝0，则x－y＝.

    查看试题解析

  • 12. 小明从镜子中看到对面电子钟如图所示，这时的时刻应是.

    查看试题解析

  • 13. 若等腰三角形的一个角为75°，则顶角为.

    查看试题解析

  • 14.

    如图，在△ABC中，AB=AD=DC，∠BAD=20°，则∠C= ．

     

    查看试题解析

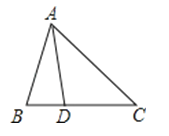  • 15. 如图，△ABC中，∠A=40°，AB的垂直平分线MN交AC于点D，∠DBC=30°，若AB=m，BC=n，则△DBC的周长为 ．

    查看试题解析

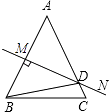  • 16. 如图，在△ABC中，角平分线BO与CO的相交点O，OE∥AB，OF∥AC，BC＝10，则△OEF的周长为.

    查看试题解析

  • 17. 如图，∠AOB是一角度为15°的钢架，要使钢架更加牢固，需在其内部添加一些钢管：EF、FG、GH…，且OE=EF=FG=GH…，在OA、OB足够长的情况下，最多能添加这样的钢管的根数为.

    查看试题解析

  • 18. 如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN＋∠ANM的度数是.

    查看试题解析

三、解答题

  • 19. 如图，在正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）.

    (1)、在图中作出△ABC关于直线MN对称的△A′B′C′；
    (2)、在（1）的结果下，连接AA′、CC′，则四边形AA′C′C的面积为.

    查看试题解析

  • 20. 如图，点B、F、C、E在一条直线上，FB=CE，AC=DF，请从下列三个条件：①AB=DE；②∠A=∠D；③∠ACB=∠DFE中选择一个合适的条件，使AB∥ED成立，并给出证明.

     

    (1)、选择的条件是（填序号）
    (2)、证明：

    查看试题解析

  • 21. 尺规作图：某学校正在进行校园环境的改造工程设计，准备在校内一块四边形花坛内栽上一棵桂花树.如图，要求桂花树的位置点P，到花坛的两边AB，BC的距离相等，并且点P到点A，D的距离也相等.请用尺规作图作出栽种桂花树的位置点P（不写作法，保留作图痕迹）.

    查看试题解析

  • 22. 如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF，

    (1)、求证：AD平分∠BAC；
    (2)、已知AC=20， BE=4，求AB的长.

    查看试题解析

  • 23. 如图，在△ABC中，边AB、AC的垂直平分线分别交BC于E、F．

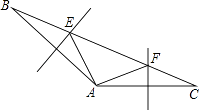    (1)、若BC=10，求△AEF周长．
    (2)、若∠BAC=128°，求∠FAE的度数．

    查看试题解析

  • 24. 如图1所示，等边△ABC中，AD是BC边上的中线，根据等腰三角形的“三线合一”特性，AD平分∠BAC，且AD⊥BC，则有∠BAD=30°，BD=CD= 12 AB.于是可得出结论“直角三角形中，30°角所对的直角边等于斜边的一半”.

    请根据从上面材料中所得到的信息解答下列问题：

    (1)、△ABC中，若∠A：∠B：∠C=1：2：3，AB= ，则BC=；
    (2)、如图2所示，在△ABC中，∠ACB=90°，BC的垂直平分线交AB于点D，垂足为E，当BD=5cm，∠B=30°时，△ACD的周长=.
    (3)、如图3所示，在△ABC中，AB=AC，∠A=120°，D是BC的中点，DE⊥AB，垂足为E，那么BE：EA=.
    (4)、如图4所示，在等边△ABC中，D、E分别是BC、AC上的点，且∠CAD=∠ABE，AD、BE交于点P，作BQ⊥AD于Q，猜想PB与PQ的数量关系，并说明理由.

    查看试题解析

  • 25. 如图， △ABC 中， AB=BC=AC=12cm ，现有两点 M 、 N 分别从点A、点B同时出发，沿三角形的边运动，已知点M的速度为1cm/s ， 点N的速度为2 cm/s.当点N第一次到达B点时， M 、 N 同时停止运动.

    (1)、点 M 、 N 运动几秒时， M 、 N 两点重合？
    (2)、点 M 、 N 运动几秒时，可得到等边三角形 △AMN ？
    (3)、当点 M 、 N 在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时 M 、 N 运动的时间.

    查看试题解析