陕西省咸阳市高新一中2020-2021学年高一上学期数学期中考试试卷

试卷更新日期：2020-11-25 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合U={1，2，3，4，5，6，7}，A={2，4，5，7}，B={3，4，5}，则(∁_UA)∪(∁_UB)等于（）

A、{1，6} B、{4，5} C、{2，3，4，5，7} D、{1，2，3，6，7}

查看试题解析
2. 设A={x|0≤x≤2}，B={y|1≤y≤2}，在下列各图中能表示从A到B的映射的是（）

A、 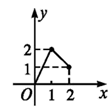B、 C、 D、

查看试题解析
3. 已知函数 $f (x) = \frac{1}{\sqrt{1 - x}}$ 的定义域 $M$ ， $g (x) = \ln (1 + x)$ 的定义域为 $N$ ，则 $M \cap N =$ （）

A、 ${x | x > - 1}$ B、 ${x | x < 1}$ C、 ${x | - 1 < x < 1}$ D、 $\emptyset$

查看试题解析
4. 若幂函数的图象过点（2， $\frac{1}{4}$ ），则它的单调递增区间是（）

A、(0，＋∞) B、[0，＋∞) C、(－∞，＋∞) D、(－∞，0)

查看试题解析
5. 函数 $y = \frac{x a^{x}}{| x |} (a > 1)$ 的图形大致形状是（）

A、 B、 C、 D、

查看试题解析
6. 某工厂去年总产值为a，计划今后5年内每年比上一年增长10%，则这5年的最后一年该厂的总产值是（）

A、1.1⁴a B、1.1⁵a C、1.1⁶a D、(1+1.1⁵)a

查看试题解析
7. 已知f(x)为R上的减函数，则满足f $(\frac{1}{x})$ >f(1)的实数x的取值范围是（）

A、(-∞，1) B、(1，+∞) C、(-∞，0)∪(0，1) D、(-∞，0)∪(1，+∞)

查看试题解析
8. 已知奇函数 $f (x)$ 在 $R$ 上是增函数，若 $a = - f (\log_{2} \frac{1}{5})$ ， $b = f (\log_{2} 4.1)$ ， $c = f (2^{0.8})$ ，则 $a ， b ， c$ 的大小关系为（）

A、 $a < b < c$ B、 $b < a < c$ C、 $c < b < a$ D、 $c < a < b$

查看试题解析
9. 函数f(x)=-x²+4x在[m，n]上的值域是[-5，4]，则m+n的取值所成的集合为（）

A、[0，6] B、[-1，1] C、[1，5] D、[1，7]

查看试题解析
10. 若函数f（x）=x³+x²-2x-2的一个正数零点附近的函数值用二分法逐次计算，参考数据如下表：
那么方程x³+x²-2x-2=0的一个近似根（精确到0.1）为（）

f（1）=-2

f（1.5）=0.625

f（1.25）=-0.984

f（1.375）=-0.260

f（1.438）=0.165

f（1.4065）=-0.052

A、1.2 B、1.3 C、1.4 D、1.5

查看试题解析
11. 已知函数 $f (x) = {\begin{array}{l} x^{2} + a x - b (x > 0) \\ 0 (x = 0) \\ g (x) (x < 0) \end{array}$ ，在区间 $(a + \frac{4}{a}, - b^{2} + 4 b)$ 上满足 $f (- x) + f (x) = 0$ ，则 $g (- \sqrt{2})$ 的值为（）

A、 $- 2 \sqrt{2}$ B、2 $\sqrt{2}$ C、 $- \sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
12. 在同一平面直角坐标系中，函数 $y = g (x)$ 的图象与 $y = e^{x}$ 的图象关于直线 $y = x$ 对称．而函数 $y = f (x)$ 的图象与 $y = g (x)$ 的图象关于 $y$ 轴对称，若 $f (m) = - 1$ ，则 $m$ 的值是（）

A、-e B、 $- \frac{1}{e}$ C、e D、 $\frac{1}{e}$

查看试题解析

二、填空题

13. 若函数 $y = f (x)$ 的定义域为[0，2]，则函数 $g (x) = \frac{f (2 x)}{x - 1}$ 的定义域是．

查看试题解析
14. 已知定义域为R的奇函数f(x)在(0,+∞)上是增函数,且f $(- \frac{1}{2})$ =0,则不等式f(log₄x)>0的解集是.

查看试题解析
15. 幂函数y=x^α ，当α取不同的正数时，在区间[0，1]上它们的图像是一族美丽的曲线(如图).设点A(1，0)，B(0，1)，连接AB，线段AB恰好被其中的两个幂函数y=x^α ， y=x^β的图像三等分，即有BM=MN=NA，那么，αβ等于.

查看试题解析
16. 下列结论中：
①定义在R上的函数f(x)在区间(-∞，0]上是增函数，在区间[0，+∞)上也是增函数，则函数f(x)在R上是增函数；②若f(2)=f(-2)，则函数f(x)不是奇函数；③函数y=x^-0.5是(0，1)上的减函数；④对应法则和值域相同的函数的定义域也相同；⑤若x₀是二次函数y=f(x)的零点，且m<x₀<n，那么f(m)f(n)<0一定成立.

写出上述所有正确结论的序号：.

查看试题解析

三、解答题

17. 设U= R,A={x | $2^{x - 3}$ ≤1},B= {x |2<x<5},C= {x|a≤x≤a+ 1}(a为实数).

(1)、求A∩B;

(2)、若B∪C=B,求a的取值范围.

查看试题解析
18. 已知 $f (x)$ = ${\begin{array}{l} f (x + 1), - 2 < x < 0 \\ 2 x + 1, 0 \leq x < 2 \\ x^{2} - 1, x \geq 2 \end{array}$ .

(1)、若 $f (a)$ =4，且a>0，求实数a的值；

(2)、求 $f (- \frac{3}{2})$ 的值.

查看试题解析
19. 已知二次函数f(x)的二次项系数为a(a<0).1,3是函数y=f(x)+2x的两个零点.若方程f(x)+6a=0有两个相等的根,求f(x)的解析式.

查看试题解析
20. 已知函数 $f (x) = \lg (\frac{m x}{x + 1} + n) (m, n \in R, m > 0)$ 的图象关于原点对称.
（Ⅰ）求 $m$ ， $n$ 的值；

（Ⅱ）若函数 $h (x) = f (2^{x}) - \lg (\frac{b}{2^{x} + 1} - 2^{x})$ 在 $(0, 1)$ 内存在零点，求实数 $b$ 的取值范围.

查看试题解析
21. 经过市场调查,某种商品在销售中有如下关系:第x(1≤x≤30,x∈N₊)天的销售价格(单位:元/件)为f(x)= ${\begin{array}{l} 40 + x, 1 \leq x \leq 10, \\ 60 - x, 10 < x \leq 30, \end{array}$ 第x天的销售量(单位:件)为g(x)=a-x(a为常数),且在第20天该商品的销售收入为1 200元(销售收入=销售价格×销售量).

(1)、求a的值,并求第15天该商品的销售收入;

(2)、求在这30天中,该商品日销售收入y的最大值.

查看试题解析
22. 已知函数f(x)=3^x,f(a+2)=27,函数g(x)=λ·2^ax-4^x的定义域为[0,2].

(1)、求a的值;

(2)、若函数g(x)在[0,2]上单调递减,求λ的取值范围;

(3)、若函数g(x)的最大值是 $\frac{1}{3}$ ,求λ的值.

查看试题解析

f（1）=-2	f（1.5）=0.625
f（1.25）=-0.984	f（1.375）=-0.260
f（1.438）=0.165	f（1.4065）=-0.052