天津市和平区2020-2021学年高三上学期数学期中考试试卷
试卷更新日期:2020-11-25 类型:期中考试
一、单选题
-
1. 设全集为 .集合A={1,3,6 },集合B={2,3,4,5}.则集合 ( ).A、{3} B、 C、 D、2. 设x∈R.则“ ”是“ ”的( ).A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分又不必要条件3. 函数 (其中 为自然对数的底数)的图象大致为( )A、
 B、
B、 C、
C、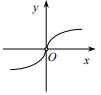 D、
D、 4. 设 .则a.b.c的大小关系是( ).A、a>c>b B、b>c>a C、c>a>b D、c>b>a5. 已知函数 的部分图象如图所示.则 的解析式为( ).
4. 设 .则a.b.c的大小关系是( ).A、a>c>b B、b>c>a C、c>a>b D、c>b>a5. 已知函数 的部分图象如图所示.则 的解析式为( ).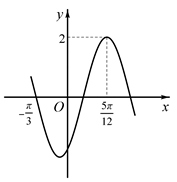 A、 B、 C、 D、6. 设数列 的前 项和 . 则 的值为( ).A、65 B、16 C、15 D、147. 已知函数 是定义在R上的奇函数,且当 时, ,则 ( )A、2 B、4 C、-2 D、-48. 若将函数 的图象向左平移 个单位长度后.得到的函数图象关于 对称.则函数 在 上的最小值是( ).A、-1 B、 C、 D、09. 已知函数 在 上单调递增.且关于 的方程 恰有两个不相等的实数解.则实数 的取值范围是( ).A、 B、 C、 D、
A、 B、 C、 D、6. 设数列 的前 项和 . 则 的值为( ).A、65 B、16 C、15 D、147. 已知函数 是定义在R上的奇函数,且当 时, ,则 ( )A、2 B、4 C、-2 D、-48. 若将函数 的图象向左平移 个单位长度后.得到的函数图象关于 对称.则函数 在 上的最小值是( ).A、-1 B、 C、 D、09. 已知函数 在 上单调递增.且关于 的方程 恰有两个不相等的实数解.则实数 的取值范围是( ).A、 B、 C、 D、二、填空题
-
10. 设i是虚数单位.复数 .11. 都成立.则 的取值范围是 .12. 在 中. .则 的面积等于 .13. 已知 为等差数列, 为其前 项和. .若 .则 的值为 .14. 已知 均为正实数. .则 的最小值为 .15. 若函数 在 上为减函数.则实数 的取值范围是 .
三、解答题
-
16. 已知函数 为二次函数. 的图象过点 .对称轴为 .函数 在 上的最小值为 .
(Ⅰ)求 的解析式;
(Ⅱ)当 时.求函数 的最小值(用 表示).
17. 在 中,内角 所对的边分别为 已知 .(Ⅰ)求角 的大小;
(Ⅱ)设 , . 求 和 的值.