江西省宜春市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )A、0.25×10-5 B、2.5×10-5 C、2.5×10-6 D、2.5×10-72. 下列运算中,正确的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、代数式 是分式 B、分式 中 , 都扩大3倍,分式的值不变 C、分式 有意义 D、分式 是最简分式4. 若 是完全平方式,则m的值等于( ).A、3 B、-5 C、7 D、7或-15. 如图点 在 内,且到三边的距离相等.若 ,则 等于( )
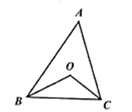 A、 B、 C、 D、6. 如图1、2、3中,点 、 分别是正 、正方形 、正五边形 中以 点为顶点的相邻两边上的点,且 , 交 于 点, 的度数分别为 , , ,若其余条件不变,在正九边形 中, 的度数是( )
A、 B、 C、 D、6. 如图1、2、3中,点 、 分别是正 、正方形 、正五边形 中以 点为顶点的相邻两边上的点,且 , 交 于 点, 的度数分别为 , , ,若其余条件不变,在正九边形 中, 的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 分解因式:8. 计算: .9. 如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件能用SAS说明△ABC≌△DEF.
 10. 如图,在 中, , , 垂直平分 ,点 为直线 上的任一点,则 周长的最小值是
10. 如图,在 中, , , 垂直平分 ,点 为直线 上的任一点,则 周长的最小值是 11. 如图,在 中, , ,点 的坐标为 ,点 的坐标为 ,点 的坐标是.
11. 如图,在 中, , ,点 的坐标为 ,点 的坐标为 ,点 的坐标是. 12. 如图, 是等边三角形,点 是 边的中点,点 在直线 上,若 是轴对称图形,则 的度数为
12. 如图, 是等边三角形,点 是 边的中点,点 在直线 上,若 是轴对称图形,则 的度数为
三、解答题
-
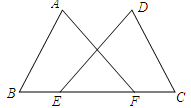
13.(1)、计算:(2)、解方程:14. 先化简,再求值: ,其中15. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
 16. 如图,在 中, 是 的角平分线, ,交 于点 , , ,求 的度数
16. 如图,在 中, 是 的角平分线, ,交 于点 , , ,求 的度数 17. 如图,在正五边形ABCDE中,请仅用无刻度的直尺 , 分别按下列要求作图。
17. 如图,在正五边形ABCDE中,请仅用无刻度的直尺 , 分别按下列要求作图。
 (1)、在图1中,画出过点A的正五边形的对称轴;(2)、在图2中,画出一个以点C为顶点的720的角.18. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图,点 , , 在同一条直线上,连结DC
(1)、在图1中,画出过点A的正五边形的对称轴;(2)、在图2中,画出一个以点C为顶点的720的角.18. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图,点 , , 在同一条直线上,连结DC (1)、请判断 与 的位置关系,并证明(2)、若 , ,求 的面积19. 某高速公路有 的路段需要维修,拟安排甲、乙两个工程队合作完成,规定工期不得超过一个月(30天) ,已知甲队每天维修公路的长度是乙队每天维修公路长度的2倍,并且在各自独立完成长度为 公路的维修时,甲队比乙队少用6天(1)、求甲乙两工程队每天能完成维修公路的长度分别是多少(2)、若甲队的工程费用为每天2万元,乙队每天的工程费用为1.2万元,15 天后乙队另有任务,余下工程由甲队完成,请你判断能否在规定的工期完成且总费用不超过80万元20. 如图在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)、请判断 与 的位置关系,并证明(2)、若 , ,求 的面积19. 某高速公路有 的路段需要维修,拟安排甲、乙两个工程队合作完成,规定工期不得超过一个月(30天) ,已知甲队每天维修公路的长度是乙队每天维修公路长度的2倍,并且在各自独立完成长度为 公路的维修时,甲队比乙队少用6天(1)、求甲乙两工程队每天能完成维修公路的长度分别是多少(2)、若甲队的工程费用为每天2万元,乙队每天的工程费用为1.2万元,15 天后乙队另有任务,余下工程由甲队完成,请你判断能否在规定的工期完成且总费用不超过80万元20. 如图在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.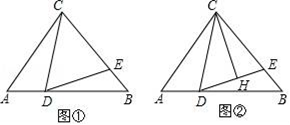 (1)、如图①,若BC=BD,求证:CD=DE;(2)、如图②,过点C作CH⊥DE,垂足为H,若CD=BD,EH=1,求DE﹣BE的值.21. 如图, 是边长为9的等边三角形, 是 边上一动点,由 向 运动(与 、 不重合), 是 延长线上一动点,与点 同时以相同的速度由 向 延长线方向运动( 不与 重合),过 作 于 ,连接 交 于
(1)、如图①,若BC=BD,求证:CD=DE;(2)、如图②,过点C作CH⊥DE,垂足为H,若CD=BD,EH=1,求DE﹣BE的值.21. 如图, 是边长为9的等边三角形, 是 边上一动点,由 向 运动(与 、 不重合), 是 延长线上一动点,与点 同时以相同的速度由 向 延长线方向运动( 不与 重合),过 作 于 ,连接 交 于 (1)、若 时,求 的长(2)、当点 , 运动时,线段 与线段 是否相等?请说明理由(3)、在运动过程中线段 的长是否发生变化?如果不变,求出线段 的长;如果发生变化,请说明理由
(1)、若 时,求 的长(2)、当点 , 运动时,线段 与线段 是否相等?请说明理由(3)、在运动过程中线段 的长是否发生变化?如果不变,求出线段 的长;如果发生变化,请说明理由