江西省萍乡市2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-24 类型：期末考试

进入出卷网下载

一、单选题

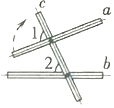
1. 下列根式中，最简二次根式是（）

A、 $\sqrt{8}$ B、 $\sqrt{10}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{12}$

查看试题解析
2. $Δ A B C$ 中， $∠ A ， ∠ B ， ∠ C$ 的对边分别是 $a ， b ， c$ ，且 $a^{2} - b^{2} = c^{2}$ ，则下列说法正确的是（）

A、 $∠ C$ 是直角 B、 $∠ B$ 是直角 C、 $∠ A$ 是直角 D、 $∠ A$ 是锐角

查看试题解析
3. 下列关系式中， $y$ 不是 $x$ 的函数的是（）

A、 $y = 3 x + 1$ B、 $y = \frac{2}{x}$ C、 $y = - \frac{1}{2} x$ D、 $| y | = x$

查看试题解析
4. 下列运算中，正确的是（）

A、 $\sqrt{4 \frac{1}{9}} = 2 \frac{1}{3}$ B、 $- \sqrt{{(- \frac{1}{2})}^{2}} = - \frac{1}{2}$ C、 $\sqrt{6^{2} + 8^{2}} = \pm 10$ D、 $\sqrt[3]{64} = 8$

查看试题解析
5. 若点 $A (a - 2, 3)$ 和点 $B (- 1, b + 5)$ 关于 $x$ 轴对称，则点 $C (a, b)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是（）

A、10° B、20° C、50° D、70°

查看试题解析
7. 下列数据的方差最大的是（）

A、3，3，6，9，9 B、4，5，6，7，8 C、5，6，6，6，7 D、6，6，6，6，6

查看试题解析
8. 小颖和小亮在做一道关于整数减法的作业题，小亮将被减数后面多加了一个0，得到的差为750；小颖将减数后面多加了一个0，得到的差为-420，则这道减法题的正确结果为（）

A、-30 B、-20 C、20 D、30

查看试题解析
9. 圆柱形容器高为18 $c m$ ，底面周长为24 $c m$ ，在杯内壁离杯底4 $c m$ 的 $B$ 处有一滴蜂蜜，此时，一只蚂蚁正好在杯外壁，离杯上沿2 $c m$ 与蜂蜜相对的 $A$ 处，则蚂蚁从外壁 $A$ 处到内壁 $B$ 处的最短距离为（）

A、19 $c m$ B、20 $c m$ C、21 $c m$ D、22 $c m$

查看试题解析
10. 一辆客车从甲地开住乙地，一辆出租车从乙地开往甲地，两车同时出发，两车距甲地的距离y（千米）与行驶时间式（小时）之间的函数图象如图所示，则下列说法中错误的是（）

A、客车比出租车晚4小时到达目的地 B、客车速度为60千米时，出租车速度为100千米/时 C、两车出发后3.75小时相遇 D、两车相遇时客车距乙地还有225千米

查看试题解析

二、填空题

11. 若 $2 a - 1$ 的平方根是±3，则 $a =$ ．

查看试题解析
12. 如图，四边形ABCD是正方形，AE⊥BE于点E ，且AE＝3，BE＝4，则阴影部分的面积是．

查看试题解析
13. 若点 $P (5 + m ， m - 3)$ 在第二、四象限角平分线上，则点 $P$ 的坐标为．

查看试题解析
14. 有5个从小到大排列的正整数，中位数是3，唯一的众数是8，则这5个数的平均数为．

查看试题解析
15. 若关于 $x ， y$ 的二元一次方程组 ${\begin{array}{l} x + 2 y = k \\ 2 x + 3 y = 1 \end{array}$ 的解是一对相反数，则实数 $k =$ ．

查看试题解析
16. $Δ A B C$ 中， $A B = A C$ ， $∠ A = 30^{\circ}$ ，点 $E$ 为 $B C$ 延长线上一点， $∠ A B C$ 与 $∠ A C E$ 的平分线相交于点 $D$ ，则 $∠ D$ 的度数为．

查看试题解析
17. 若 $a = \sqrt{1003} + \sqrt{997}$ ， $b = \sqrt{1001} + \sqrt{999}$ ， $c = 2 \sqrt{1001}$ ，则 $a ， b ， c$ 的大小关系用“＜”号排列为．

查看试题解析
18. 已知A、B、C、D是平面坐标系中坐标轴上的点，且△AOB≌△COD ．设直线AB的表达式为y₁=k₁x+b₁ ，直线CD的表达式为y₂=k₂x+b₂ ，则k₁k₂= ．

查看试题解析

三、解答题

19.

(1)、计算： ${(\sqrt{2} + 1)}^{2} - \sqrt{3} \times (\sqrt{6} - \sqrt{3}) + 2 \sqrt{0.5}$

(2)、若 $| 3 x - 2 y - 1 | + \sqrt{x + y - 2} = 0$ ，求 $x ， y$ 的值．

查看试题解析
20. 如图，已知∠1+∠2＝180°，∠3＝∠B，试判断∠AED与∠ACB的大小关系，并说明理由．

查看试题解析
21. 如图，在△ABC中，∠ABC=90°，AB=6cm，AD=24cm，BC与CD的长度之和为34cm，其中C是直线l上的一个动点，请你探究当C离点B有多远时，△ACD是以DC为斜边的直角三角形.

查看试题解析
22. 水龙头关闭不紧会造成滴水，小明用可以显示水量的容器做图①所示的试验，并根据试验数据绘制出图②所示的容器内盛水量W（L）与滴水时间t（h）的函数关系图象，请结合图象解答下列问题：

图 ① 图②

(1)、容器内原有水多少？

(2)、求W与t之间的函数关系式，并计算在这种滴水状态下一天的滴水量是多少升？

查看试题解析
23. 如图，在 $Δ A B C$ 中， $∠ 1 = 100^{\circ}$ ， $∠ C = 80^{\circ}$ ， $∠ 2 = \frac{1}{2} ∠ 3$ ， $B E$ 平分 $∠ A B C$ 交 $A D$ 于 $E$ ，求 $∠ 4$ 的度数．

查看试题解析
24. 某班将举行“数学知识竞赛”活动，班长安排小明购买奖品，下面两图是小明买回奖品时与班长的对话情境：

请根据上面的信息，解决问题：

(1)、试计算两种笔记本各买了多少本？

(2)、请你解释：小明为什么不可能找回68元？

查看试题解析

25. 某中学举行“中国梦·校园好声音”歌手大赛，高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩（满分100）如下图所示：

根据图示信息，整理分析数据如下表：

	平均数（分）	中位数（分）	众数（分）
初中部	$a$	85	$c$
高中部	85	$b$	100

（说明：图中虚线部分的间隔距离均相等）

(1)、求出表格中

a ， b ， c

的值；

(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

(3)、计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．

查看试题解析

26. 如图，把长方形纸片 $O A B C$ 放入平面直角坐标系中，使 $O A ， O C$ 分别落在 $x ， y$ 轴的的正半轴上，连接 $A C$ ，且 $A C = 4 \sqrt{5}$ ， $A O = 2 C O$ ．

(1)、求点 $A ， C$ 的坐标；

(2)、将纸片 $O A B C$ 折叠，使点 $A$ 与点 $C$ 重合（折痕为 $E F$ ），求折叠后纸片重叠部分 $Δ C E F$ 的面积；

(3)、求 $E F$ 所在直线的函数表达式，并求出对角线 $A C$ 与折痕 $E F$ 交点 $D$ 的坐标．

查看试题解析