江西省南昌市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 若分式 有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列四个腾讯软件图标中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 若 , 是等腰三角形 的两边长,且满足关系式 ,则 的周长是( )A、10 B、11 C、10或11 D、11或125. 在平面直角坐标系中,点 关于直线 的对称点坐标是( )A、 B、 C、 D、6. 如图, , ,当添加一个条件时,仍不能判定 ≌ ,则这个添加的条件是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 若 , 是等腰三角形 的两边长,且满足关系式 ,则 的周长是( )A、10 B、11 C、10或11 D、11或125. 在平面直角坐标系中,点 关于直线 的对称点坐标是( )A、 B、 C、 D、6. 如图, , ,当添加一个条件时,仍不能判定 ≌ ,则这个添加的条件是( ) A、 B、 C、 D、7. 化简 的结果是( )A、 B、 C、 D、8. 如图,在 中, , 、 、 分别是 、 、 上的点,且 , ,若 ,则 的度数是( )
A、 B、 C、 D、7. 化简 的结果是( )A、 B、 C、 D、8. 如图,在 中, , 、 、 分别是 、 、 上的点,且 , ,若 ,则 的度数是( )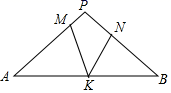 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
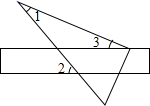
9. 若多项式 能用完全平方公式因式分解,则 的值是 .10. 将三角尺的直角顶点放在直尺的一边上,若 , ,则 的度数是 .
 11. 若 , ,则 的值是 .12. 如图,钝角 的面积为12,最长边 , 平分 ,点 、 分别是 、 上的动点,则 的最小值是 .
11. 若 , ,则 的值是 .12. 如图,钝角 的面积为12,最长边 , 平分 ,点 、 分别是 、 上的动点,则 的最小值是 .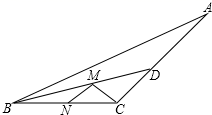 13. 若 ,则 的值是 .14. 有一个三角形纸片 , ,点 是 边上一点,沿 方向剪开三角形纸片后,发现所得的两纸片均为等腰三角形,则 的度数可以是 .
13. 若 ,则 的值是 .14. 有一个三角形纸片 , ,点 是 边上一点,沿 方向剪开三角形纸片后,发现所得的两纸片均为等腰三角形,则 的度数可以是 .
三、解答题
-
15.(1)、计算:(2)、分解因式:16.(1)、求值: ,其中(2)、解方程:17. 已知 , ,(1)、求证: ;(2)、求 的值.18. 如图,已知 ≌ ,且 、 、 、 四点在同一直线上.
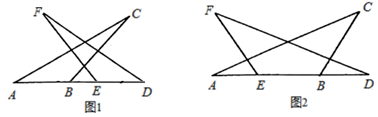 (1)、在图1中,请你用无刻度的直尺作出线段 的垂直平分线;(2)、在图2中,请你用无刻度的直尺作出线段 的垂直平分线.19. 如图1的两个长方形可以按不同的形式拼成图2和图3两个图形.
(1)、在图1中,请你用无刻度的直尺作出线段 的垂直平分线;(2)、在图2中,请你用无刻度的直尺作出线段 的垂直平分线.19. 如图1的两个长方形可以按不同的形式拼成图2和图3两个图形.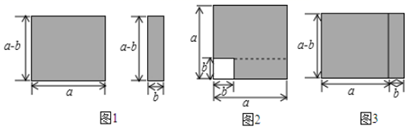 (1)、在图2中的阴影部分面积 可表示为 , 在图3中的阴影部分的面积 可表示为 , 由这两个阴影部分的面积得到的一个等式是
(1)、在图2中的阴影部分面积 可表示为 , 在图3中的阴影部分的面积 可表示为 , 由这两个阴影部分的面积得到的一个等式是A.
B.
C.
(2)、根据你得到的等式解决下面的问题:①计算: ;
②解方程:
20. 为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾.若租用甲、乙两车运送,两车各运6趟可完成,需支付运费1800元.已知甲、乙两车单独运完此堆垃圾,乙车所运的趟数是甲车的1.5倍,且乙车每趟运费比甲车少100元.(1)、求甲、乙两车单独运完此堆垃圾各需多少趟?(2)、若单独租用一台车,租用哪台车更合算,请你通过计算说明.21. 如图1,在 和 中, , , ,连接 、 .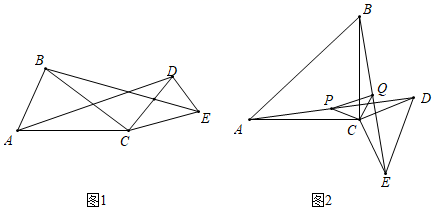 (1)、求证: ≌ ;(2)、如图2,当 时,取 、 的中点 、 ,连接 、 、 ,判断 的形状,并加以证明.22. 如图,在等边 中, ,现有两点 、 分别从点 、 同时出发,沿三角形的边运动,已知点 的速度为 ,点 的速度为 .当点 第一次回到点 时,点 、 同时停止运动,设运动时间为 .
(1)、求证: ≌ ;(2)、如图2,当 时,取 、 的中点 、 ,连接 、 、 ,判断 的形状,并加以证明.22. 如图,在等边 中, ,现有两点 、 分别从点 、 同时出发,沿三角形的边运动,已知点 的速度为 ,点 的速度为 .当点 第一次回到点 时,点 、 同时停止运动,设运动时间为 .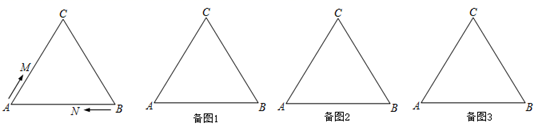 (1)、当 为何值时, 、 两点重合;(2)、当点 、 分别在 、 边上运动, 的形状会不断发生变化.
(1)、当 为何值时, 、 两点重合;(2)、当点 、 分别在 、 边上运动, 的形状会不断发生变化.①当 为何值时, 是等边三角形;
②当 为何值时, 是直角三角形;
(3)、若点 、 都在 边上运动,当存在以 为底边的等腰 时,求 的值.