江西省吉安市吉州区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 点P(﹣3,﹣4)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 如图,将一张含有 角的三角形纸片的两个顶点放在直尺的两条对边上,若 ,则 的度数是( )
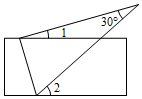 A、 B、 C、 D、3. 在实数 , , , , ,0中,无理数的个数为( )A、1个 B、2个 C、3个 D、4个4. 如图,在 中,其中 , 的平分线 交 于点 , 是 的垂直平分线,点 是垂足.已知 ,则图中长度为 的线段有( )
A、 B、 C、 D、3. 在实数 , , , , ,0中,无理数的个数为( )A、1个 B、2个 C、3个 D、4个4. 如图,在 中,其中 , 的平分线 交 于点 , 是 的垂直平分线,点 是垂足.已知 ,则图中长度为 的线段有( ) A、1条 B、2条 C、3条 D、4条5. 甲、乙两名同学的5次射击训练成绩(单位:环)如下表:
A、1条 B、2条 C、3条 D、4条5. 甲、乙两名同学的5次射击训练成绩(单位:环)如下表:甲
7
8
9
8
8
乙
6
10
9
7
8
比较甲、乙这5次射击成绩的方差,结果为:甲的方差( )乙的方差.
A、大于 B、小于 C、等于 D、无法确定6. 已知,如图点A(1,1),B(2,﹣3),点P为x轴上一点,当|PA﹣PB|最大时,点P的坐标为( ) A、(﹣1,0) B、( ,0) C、( ,0) D、(1,0)
A、(﹣1,0) B、( ,0) C、( ,0) D、(1,0)二、填空题
-
7. 4的算术平方根是 , 9的平方根是 , ﹣27的立方根是 .8. 若点M(a,﹣1)与点N(2,b)关于y轴对称,则a+b的值是9. 如果 ,那么 值是 .10. 如图,长方体的长为 ,宽为 ,高为 ,点 离点 的距离为 ,一只蚂蚁如果要沿着长方体的表面从点 爬到点 ,需要爬行的最短距离是。
 11. 某活动小组购买了4个篮球和5个足球,一共花费了435元,其中篮球的单价比足球的单价多3元,求篮球的单价和足球的单价.设篮球的单价为x元,足球的单价为y元,依题意,可列方程组为 .12. 如图,直线y=﹣ x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为 .
11. 某活动小组购买了4个篮球和5个足球,一共花费了435元,其中篮球的单价比足球的单价多3元,求篮球的单价和足球的单价.设篮球的单价为x元,足球的单价为y元,依题意,可列方程组为 .12. 如图,直线y=﹣ x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为 .
三、解答题
-
13.(1)、(2)、解方程组:14. 如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.

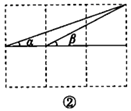 (1)、如图①, , , 是三个格点(即小正方形的顶点),判断 与 的位置关系,并说明理由;(2)、如图②,连接三格和两格的对角线,求 的度数(要求:画出示意图,并写出证明过程).15. 如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
(1)、如图①, , , 是三个格点(即小正方形的顶点),判断 与 的位置关系,并说明理由;(2)、如图②,连接三格和两格的对角线,求 的度数(要求:画出示意图,并写出证明过程).15. 如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.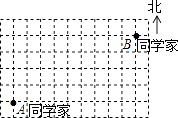 (1)、以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系:(2)、B同学家的坐标是;(3)、在你所建的直角坐标系中,如果C同学家的坐标为(﹣150,100),请你在图中描出表示C同学家的点.16. 为了比较 +1与 的大小,小伍和小陆两名同学对这个问题分别进行了研究.
(1)、以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系:(2)、B同学家的坐标是;(3)、在你所建的直角坐标系中,如果C同学家的坐标为(﹣150,100),请你在图中描出表示C同学家的点.16. 为了比较 +1与 的大小,小伍和小陆两名同学对这个问题分别进行了研究.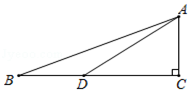 (1)、小伍同学利用计算器得到了 , ,所以确定 +1 (填“>”或“<”或“=”)(2)、小陆同学受到前面学习在数轴上用点表示无理数的启发,构造出所示的图形,其中∠C=90°,BC=3,D在BC上且BD=AC=1.请你利用此图进行计算与推理,帮小陆同学对 +1和 的大小做出准确的判断.17. 如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度 (单位: )与下行时间 (单位: )之间具有函数关系 ,乙离一楼地面的高度 (单位: )与下行时间 (单位: )的函数关系如图2所示.
(1)、小伍同学利用计算器得到了 , ,所以确定 +1 (填“>”或“<”或“=”)(2)、小陆同学受到前面学习在数轴上用点表示无理数的启发,构造出所示的图形,其中∠C=90°,BC=3,D在BC上且BD=AC=1.请你利用此图进行计算与推理,帮小陆同学对 +1和 的大小做出准确的判断.17. 如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度 (单位: )与下行时间 (单位: )之间具有函数关系 ,乙离一楼地面的高度 (单位: )与下行时间 (单位: )的函数关系如图2所示.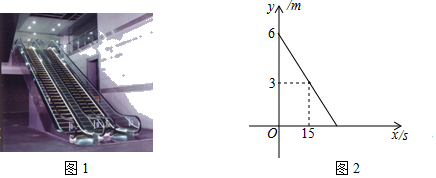 (1)、求 关于 的函数解析式;(2)、请通过计算说明甲、乙两人谁先到达一楼地面.18. 为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
(1)、求 关于 的函数解析式;(2)、请通过计算说明甲、乙两人谁先到达一楼地面.18. 为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
七年级
0
1
0
a
7
1
八年级
1
0
0
7
b
2
分析数据:
平均数
众数
中位数
七年级
78
75
八年级
78
80.5
应用数据:
(1)、由上表填空:a= , b= , c= , d=.(2)、估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?(3)、你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.19. 亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.(1)、计划调配36座新能源客车多少辆?该大学共有多少名志愿者?(2)、若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?20. 如图,已知 与 都是等腰直角三角形,其中 , 为 边上一点. (1)、试判断 与 的大小关系,并说明理由;(2)、求证: .21. 探究与发现:如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,
(1)、试判断 与 的大小关系,并说明理由;(2)、求证: .21. 探究与发现:如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”, (1)、观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;(2)、请你直接利用以上结论,解决以下三个问题:
(1)、观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;(2)、请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX等于多少度;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9 , 若∠BDC=133°,∠BG1C=70°,求∠A的度数.
22. 阅读材料:善于思考的小军在解方程组 时,采用了一种“整体代换”的解法:解:将方程②变形: ,即 ③
把方程①代入③得: ,∴ ,
所 代入①得 ,∴方程组的解为 ,
请你解决以下问题:
(1)、模仿小军的“整体代换”法解方程组 ,(2)、已知 满足方程组 ,求 的值 和的值.23. 直线 与 轴相交于点 ,与 轴相交于点 . (1)、求直线 与坐标轴围成的面积;(2)、在 轴上一动点 ,使 是等腰三角形;请直接写出所有 点的坐标,并求出如图所示 时点 的坐标;(3)、直线 与直线 相交于点 ,与 轴相交于点 ;点 是直线 上一点,若 的面积是 的面积的两倍,求点 的坐标.
(1)、求直线 与坐标轴围成的面积;(2)、在 轴上一动点 ,使 是等腰三角形;请直接写出所有 点的坐标,并求出如图所示 时点 的坐标;(3)、直线 与直线 相交于点 ,与 轴相交于点 ;点 是直线 上一点,若 的面积是 的面积的两倍,求点 的坐标.