江西省赣州市兴国县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 如图,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形具有稳定性的是( )A、三角形 B、四边形 C、五边形 D、六边形3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,在△ABC中,∠C=90°,AD平分∠BAC , AE=AC , 下列结论中错误的是( )
2. 下列图形具有稳定性的是( )A、三角形 B、四边形 C、五边形 D、六边形3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,在△ABC中,∠C=90°,AD平分∠BAC , AE=AC , 下列结论中错误的是( ) A、DC=DE B、∠AED=90° C、∠ADE=∠ADC D、DB=DC5. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
A、DC=DE B、∠AED=90° C、∠ADE=∠ADC D、DB=DC5. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )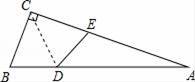 A、44° B、60° C、67° D、77°6. 某电子元件厂准备生产4600个电子元件,甲车间独立生产了一半后,由于要尽快投入市场,乙车间也加入该电子元件的生产,若乙车间每天生产的电子元件是甲车间的1.3倍,结果用33天完成任务,问甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可得方程为( )A、 B、 C、 D、
A、44° B、60° C、67° D、77°6. 某电子元件厂准备生产4600个电子元件,甲车间独立生产了一半后,由于要尽快投入市场,乙车间也加入该电子元件的生产,若乙车间每天生产的电子元件是甲车间的1.3倍,结果用33天完成任务,问甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可得方程为( )A、 B、 C、 D、二、填空题
-
7. 若分式 有意义,则 的取值范围是 .8. 若x2+ax+4是完全平方式,则a= .9. 点P(4,5)关于x轴对称的点的坐标是 .10. 如图,在△ABC中,∠B=30°,ED垂直平分BC , ED=3.则CE的长为 .
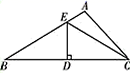 11. 已知:实数m,n满足:m+n=3,mn=2.则(1+m)(1+n)的值等于 .12.
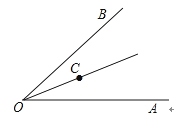
11. 已知:实数m,n满足:m+n=3,mn=2.则(1+m)(1+n)的值等于 .12.如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为
 13. 如果实数x满足 ,那么代数式 的值为.14. 已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF//BC交 AB于点E,交AC于点F.求证:BE+CF=EF.
13. 如果实数x满足 ,那么代数式 的值为.14. 已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF//BC交 AB于点E,交AC于点F.求证:BE+CF=EF.
三、解答题
-
15. 计算:(1)、(2)、16. 解方程:17. 如图,在ΔABC与ΔDCB 中, AC与BD 交于点E , 且,∠A=∠D , AB=DC.求证:ΔABE≌ΔDCE
 18. 如图所示,△ABC的顶点在正方形格点上.
18. 如图所示,△ABC的顶点在正方形格点上. (1)、写出顶点C的坐标;(2)、作△ABC关于y轴对称的△A1B1C1 .19. 如图,∠ACB=90°,AC=BC , AD⊥CE , BE⊥CE , 垂足分别为D , E .
(1)、写出顶点C的坐标;(2)、作△ABC关于y轴对称的△A1B1C1 .19. 如图,∠ACB=90°,AC=BC , AD⊥CE , BE⊥CE , 垂足分别为D , E . (1)、证明:△BCE≌△CAD;(2)、若AD=15cm , BE=8cm , 求DE的长.20. 某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.(1)、这两次各购进这种衬衫多少件?(2)、若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?21. 如图,AC平分∠BCD , AB=AD , AE⊥BC于E , AF⊥CD于F.
(1)、证明:△BCE≌△CAD;(2)、若AD=15cm , BE=8cm , 求DE的长.20. 某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.(1)、这两次各购进这种衬衫多少件?(2)、若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?21. 如图,AC平分∠BCD , AB=AD , AE⊥BC于E , AF⊥CD于F. (1)、若∠ABE=60°,求∠CDA的度数;(2)、若AE=2,BE=1,CD=4.求四边形AECD的面积.22. 在日历上,我们可以发现其中某些数满足一定的规律,如图是2020年1月份的日历.(1)、如图所选择的两组四个数,分别将每组数中相对的两数相乘,再相减,例如:9×11﹣3×17= , 12×14﹣6×20= , 不难发现,结果都是 .
(1)、若∠ABE=60°,求∠CDA的度数;(2)、若AE=2,BE=1,CD=4.求四边形AECD的面积.22. 在日历上,我们可以发现其中某些数满足一定的规律,如图是2020年1月份的日历.(1)、如图所选择的两组四个数,分别将每组数中相对的两数相乘,再相减,例如:9×11﹣3×17= , 12×14﹣6×20= , 不难发现,结果都是 .
请将上面三个空补充完整;
(2)、请你利用整式的运算对以上规律进行证明.23. 如图,已知A(3,0),B(0,﹣1),连接AB,过B点作AB的垂线段BC,使BA=BC,连接AC.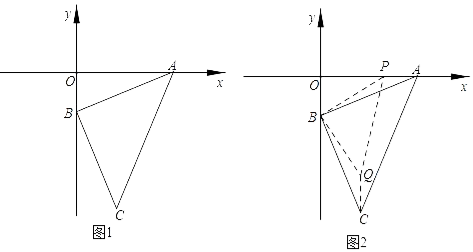 (1)、如图1,求C点坐标;(2)、如图2,若P点从A点出发沿x轴向左平移,连接BP,作等腰直角△BPQ,连接CQ,当点P在线段OA上,求证:PA=CQ;(3)、在(2)的条件下若C、P,Q三点共线,求此时∠APB的度数及P点坐标.
(1)、如图1,求C点坐标;(2)、如图2,若P点从A点出发沿x轴向左平移,连接BP,作等腰直角△BPQ,连接CQ,当点P在线段OA上,求证:PA=CQ;(3)、在(2)的条件下若C、P,Q三点共线,求此时∠APB的度数及P点坐标.