江西省赣州市宁都县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的各种线段，可以组成三角形的是（）

A、1、2、3 B、1、5、5 C、3、3、6 D、4、5、10

查看试题解析
2. 习近平书记提出的“中国梦”，这3个字中是轴对称图形的有（）

A、3个 B、2个 C、1个 D、0个

查看试题解析
3.
如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形（a>0），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为（）

A、（2a²+5a）cm² B、（3a+15）cm² C、（6a+9）cm² D、（6a+15）cm²

查看试题解析
4. 如图，∠ACB=90⁰ ， AC=BC，BE⊥CE，AD⊥CE于D，AD=2.5cm，DE=1.7cm，则BE=（）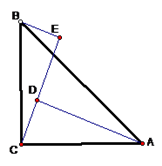

A、1cm B、0.8cm C、4.2cm D、1.5cm

查看试题解析
5. 已知关于 $x$ 的分式方程 $\frac{2 x - m}{x - 3} = 1$ 的解是非正数，则 $m$ 的取值范围是（）

A、 $m \leq 3$ B、 $m < 3$ C、 $m > - 3$ D、 $m \geq - 3$

查看试题解析
6. 用大小相同的小三角形摆成如图所示的图案，按照这样的规律摆放，则第12个图案中共有小三角形的个数是（）

A、34 B、40 C、37 D、35

查看试题解析

二、填空题

7. 计算：（﹣3）⁰÷（﹣2）²= ．

查看试题解析
8. 点A(2，－3)关于x轴对称的点的坐标是．

查看试题解析
9. 如图是某中学某班的班徽设计图案，其形状可以近似看作正五边形，则每一个内角为度；

查看试题解析
10. 因式分解：x﹣x²= ．

查看试题解析
11. 定义：形如a+bi的数称为复数（其中a和b为实数，i为虚数单位，规定i²＝﹣1），a称为复数的实部，b称为复数的虚部．复数可以进行四则运算，运算的结果还是一个复数.如（1+3i）²＝1²+2×1×3i+（3i）²＝1+6i+9i²＝1+6i﹣9＝﹣8+6i，因此（1+3i）²的实部是﹣8，虚部是6．已知复数（3﹣mi）²的虚部是12，则实部是．

查看试题解析
12. 如图，△ADB、△BCD都是等边三角形，点E，F分别是AB，AD上两个动点，满足AE=DF．连接BF与DE相交于点G，CH⊥BF，垂足为H，连接CG．若DG= ，BG= ，且、满足下列关系： $a^{2} + b^{2} = 5$ ， $a b = 2$ ，则GH= ．

查看试题解析

三、解答题

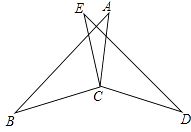
13. 计算：(2a＋b)(2a－b)＋b(2a＋b)－8a²b÷2b

查看试题解析
14. 如图，已知：EC=AC，∠BCE=∠DCA，∠A=∠E．求证：∠B=∠D．

查看试题解析
15. 数学课上老师出了一道题：计算296²的值，喜欢数学的小亮举手做出这道题，他的解题过程如下：
296²=(300－4)²=300²－2×300×(－4)+4²

=90000+2400+16=92416

老师表扬小亮积极发言的同时，也指出了解题中的不符合题意，你认为小亮的解题过程错在哪儿，并给出正确的答案.

查看试题解析
16. 先化简，再求值： $(\frac{3 x + 4}{x^{2} - 1} - \frac{2}{x - 1}) \div \frac{x + 2}{x^{2} - 2 x + 1}$ ，其中 $x = - 3$ ．

查看试题解析
17. 如图，已知：在平面直角坐标系中，每个小正方形的边长为1，△ABC的顶点都在格点上，点A的坐标为（－3，2）.请按要求分别完成下列各小题：

(1)、把△ABC向下平移7个单位，再向右平移7个单位，得到△A₁B₁C₁ ，画出△A₁B₁C₁；

(2)、画出△A₁B₁C₁关于x轴对称的△A₂B₂C₂；
画出△A₁B₁C₁关于y轴对称的△A₃B₃C₃；

(3)、求△ABC的面积.

查看试题解析
18. 如图所示，△ABC中，AB=BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F．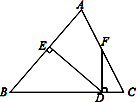

(1)、若∠AFD=155°，求∠EDF的度数；

(2)、若点F是AC的中点，求证：∠CFD= $\frac{1}{2}$ ∠B．

查看试题解析
19. 某文具店老板第一次用1000元购进一批文具，很快销售完毕；第二次购进时发现每件文具进价比第一次上涨了2 5元．老板用2500元购进了第二批文具，所购进文具的数量是第一次购进数量的2倍，同样很快销售完毕，两批文具的售价均为每件15元．

(1)、问第二次购进了多少件文具？

(2)、文具店老板第一次购进的文具有3% 的损耗，第二次购进的文具有5% 的损耗，问文具店老板在这两笔生意中是盈利还是亏本？请说明理由．

查看试题解析
20. 阅读下列材料：小明为了计算1+2+2²+……+2²⁰¹⁸+2²⁰¹⁹的值，采用以下方法：
设S=1+2+2²+……+2²⁰¹⁸+2²⁰¹⁹①

则2S=2+2²+……+2²⁰¹⁹+2²⁰²⁰②

②-①得，2S-S=S=2²⁰²⁰-1

请仿照小明的方法解决以下问题：

(1)、1+2+2²+……+2⁹=；

(2)、3+3²+……+3¹⁰=；

(3)、求1+a+a²+……+aⁿ的和(a＞0，n是正整数，请写出计算过程).

查看试题解析
21. 如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CF，垂足为F.

(1)、若AC＝10，求四边形ABCD的面积；

(2)、求证：AC平分∠ECF；

(3)、求证：CE＝2AF.

查看试题解析
22.

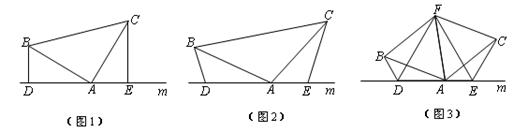(1)、如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E.证明：DE=BD+CE.

(2)、如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC= $α$ ，其中 $α$ 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立，请你给出证明；若不成立，请说明理由.

(3)、拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

查看试题解析