江西省赣州市大余县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 下列图标是节水、节能、低碳和绿色食品的标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 人体一根头发的直径约为 米,这个数字用科学记数法表示正确的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 将一副常规的三角尺按如图方式放置,则图中∠1的度数为( )
2. 人体一根头发的直径约为 米,这个数字用科学记数法表示正确的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 将一副常规的三角尺按如图方式放置,则图中∠1的度数为( )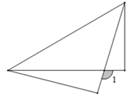 A、95° B、100° C、105° D、115°5. 如图,在△ABC中,∠ACB=90°,∠A=26°,BC=BD , 则∠ACD的度数是( )
A、95° B、100° C、105° D、115°5. 如图,在△ABC中,∠ACB=90°,∠A=26°,BC=BD , 则∠ACD的度数是( )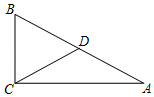 A、64° B、42° C、32° D、26°6. 如图, 于 , 于 ,若 , 平分 ,则下列结论:① ;② ;③ ;④ ,正确的有( )个
A、64° B、42° C、32° D、26°6. 如图, 于 , 于 ,若 , 平分 ,则下列结论:① ;② ;③ ;④ ,正确的有( )个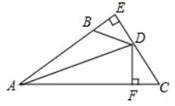 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 要使分式 有意义, 的取值应满足 .8. 因式分解: .9. 如图,已知CA=BD判定△ABD≌△DCA时,还需添加的条件是 .
 10. 若点A(a,1)与点B(﹣3,b)关于x轴对称,则ab=.11. 已知 , , ,比较 , , 的大小关系,用“ ”号连接为 .12. 等腰三角形的一条高与一腰的夹角为40°,则等腰三角形的一个底角为 .
10. 若点A(a,1)与点B(﹣3,b)关于x轴对称,则ab=.11. 已知 , , ,比较 , , 的大小关系,用“ ”号连接为 .12. 等腰三角形的一条高与一腰的夹角为40°,则等腰三角形的一个底角为 .三、解答题
-
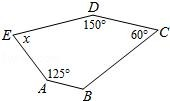
13. 因式分解:(1)、(2)、 .14. 解方程:15. 如图,在五边形ABCDE中满足 AB∥CD,求图形中的x的值.
 16. 如图,有两个长度相等的滑梯BC与EF , 滑梯BC的高AC与滑梯EF水平方向,DF的长度相等,问两个滑梯的倾斜角 与 的大小有什么关系?请说明理由.
16. 如图,有两个长度相等的滑梯BC与EF , 滑梯BC的高AC与滑梯EF水平方向,DF的长度相等,问两个滑梯的倾斜角 与 的大小有什么关系?请说明理由.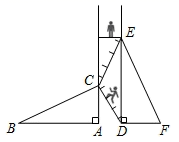 17. 在5×7的方格纸上,任意选出5个小方块涂上颜色,使整个图形(包括着色的“对称”)有:
17. 在5×7的方格纸上,任意选出5个小方块涂上颜色,使整个图形(包括着色的“对称”)有: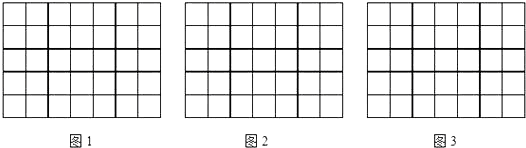
①1条对称轴;
②2条对称轴;
③4条对称轴.
18. 如图在平面直角坐标系中, 的顶点坐标分别为 , , (1)、请在图中画出 关于 轴的对称图形 ,点 、 、 的对称点分别为 、 、 ,其中 的坐标为; 的坐标为; 的坐标为 .(2)、请求出 的面积.19. 观察下列等式:
(1)、请在图中画出 关于 轴的对称图形 ,点 、 、 的对称点分别为 、 、 ,其中 的坐标为; 的坐标为; 的坐标为 .(2)、请求出 的面积.19. 观察下列等式:①32﹣31=2×31;②33﹣32=2×32;③34﹣33=2×33;④35﹣34=2×34…根据等式所反映的规律,解答下列问题:
(1)、直接写出:第⑤个等式为;(2)、猜想:第n个等式为(用含n的代数式表示),并证明.20. 如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D , BC=CE . (1)、求证:AC=CD;(2)、若AC=AE , 求∠DEC的度数.21. 某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?22. 阅读与思考:
(1)、求证:AC=CD;(2)、若AC=AE , 求∠DEC的度数.21. 某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?22. 阅读与思考:因式分解----“分组分解法”:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如,四项的多项式一般按照“两两”分组或“三一”分组进行分组分解.分析多项式的特点,恰当的分组是分组分解法的关键.
例1:“两两”分组:
我们把 和 两项分为一组, 和 两项分为一组,分别提公因式,立即解除了困难.同样.这道题也可以这样做:
例2:“三一”分组:
我们把 , , 三项分为一组,运用完全平方公式得到 ,再与-1用平方差公式分解,问题迎刃而解.
归纳总结:用分组分解法分解因式的方法是先恰当分组,然后用提公因式法或运用公式法继续分解.
请同学们在阅读材料的启发下,解答下列问题:
(1)、分解因式:① ;
②
(2)、若多项式 利用分组分解法可分解为 ,请写出 , 的值.23. 小敏与同桌小颖在课下学习中遇到这样一道数学题:“如图(1),在等边三角形 中,点 在 上,点 在 的延长线上,且 ,试确定线段 与 的大小关系,并说明理由”.小敏与小颖讨论后,进行了如下解答: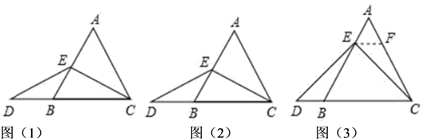 (1)、取特殊情况,探索讨论:当点 为 的中点时,如图(2),确定线段 与 的大小关系,请你写出结论: (填“ ”,“ ”或“ ”),并说明理由.(2)、特例启发,解答题目:
(1)、取特殊情况,探索讨论:当点 为 的中点时,如图(2),确定线段 与 的大小关系,请你写出结论: (填“ ”,“ ”或“ ”),并说明理由.(2)、特例启发,解答题目:解:题目中, 与 的大小关系是: (填“ ”,“ ”或“ ”).理由如下:
(3)、①如图(3),过点 作EF∥BC , 交 于点 .(请你将剩余的解答过程完成)②拓展结论,设计新题:在等边三角形 中,点 在直线 上,点 在直线 上,且 ,若△ 的边长为 , ,求 的长(请你画出图形,并直接写出结果).