福建省三明市大田县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 2的平方根为（　　）

A、4 B、±4 C、 $\sqrt{2}$ D、± $\sqrt{2}$

查看试题解析
2. 下列各数中是无理数的是（）

A、 $3.14$ B、 $\sqrt[3]{8}$ C、 $\sqrt{15}$ D、 $\sqrt{16}$

查看试题解析
3. 以下列各组数为边长，不能构成直角三角形的是（）

A、3，4，5 B、1，1， $\sqrt{2}$ C、8，12，13 D、 $\sqrt{2}$ , $\sqrt{3}$ , $\sqrt{5}$

查看试题解析
4. 将一副直角三角尺如图放置，已知AE∥BC，则∠AFD的度数是（）

A、45° B、50° C、60° D、75°

查看试题解析
5. 在共有l5人参加的演讲加比赛中，参赛选手的成绩各不相同，因此选手要想知道自己是否进入前八名，只需了解自己的成绩以及全部成绩的（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
6. 如图，围棋棋盘放在某平面直角坐标系内，已知黑棋(甲)的坐标为(﹣2，2)黑棋(乙)的坐标为(﹣1，﹣2)，则白棋(甲)的坐标是（）

A、(2，2) B、(0，1) C、(2，﹣1) D、(2，1)

查看试题解析
7. 下列四个命题中，是真命题的是（）

A、两条直线被第三条直线所截，内错角相等 B、如果∠1和∠2是对顶角，那么∠1=∠2． C、三角形的一个外角大于任何一个内角 D、无限小数都是无理数．

查看试题解析
8.
如图所示：数轴上点A所表示的数为a，则a的值是（　　）

A、 $\sqrt{5}$ +1 B、 $\sqrt{5}$ -1 C、- $\sqrt{5}$ +1 D、- $\sqrt{5}$ -1

查看试题解析
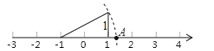9. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）

A、 ${\begin{matrix} x + y = 35 \\ 2 x + 2 y = 94 \end{matrix}$ B、 ${\begin{matrix} x + y = 35 \\ 4 x + 2 y = 94 \end{matrix}$ C、 ${\begin{matrix} x + y = 35 \\ 4 x + 4 y = 94 \end{matrix}$ D、 ${\begin{matrix} x + y = 35 \\ 2 x + 4 y = 94 \end{matrix}$

查看试题解析
10. 如图所示，已知点A(﹣1，2)是一次函数y＝kx+b（k≠0）的图象上的一点，则下列判断中正确的是（）

A、y随x的增大而减小 B、k＞0，b＜0 C、当x＜0时，y＜0 D、方程kx+b＝2的解是x＝﹣1

查看试题解析

二、填空题

11. 比较大小： $3 \sqrt{2}$ $2 \sqrt{3}$ （填“＞”或“＜”＝）.

查看试题解析
12. 若 $P (- 3 ， 2)$ ，则点P到y轴的距离为.

查看试题解析
13. 已知 ${\begin{cases} x = - 1 \\ y = 2 \end{cases}$ 是关于 $x 、 y$ 的二元一次方程 $m x - y = 3$ 的一个解，则 $m$ = ．

查看试题解析
14. 已知一组数据为：5，3，3，6，3，则这组数据的方差是．

查看试题解析
15. 如图，在一次测绘活动中，某同学站在点A处观测停放于B、C两处的小船，测得船B在点A北偏东75°方向160米处，船C在点A南偏东15°方向120米处，则船B与船C之间的距离为米．

查看试题解析
16. 如图，有一种动画程序，屏幕上正方形 $A B C D$ 是黑色区域（含正方形边界），其中四个顶点的坐标分别为 $A (1 ， 1)$ 、 $B (2 ， 1)$ 、 $C (2 ， 2)$ 、 $D (1 ， 2)$ ，用信号枪沿直线 $y = 2 x + b$ 发射信号，当信号遇到黑色区域时，区域便由黑变白，则能使黑色区域变白的b的取值范围为．

查看试题解析
17. 计算： $6 \sqrt{\frac{1}{2}} - \sqrt[3]{- 64} - (\sqrt{6} - 1) \times \sqrt{3}$

查看试题解析

三、解答题

18. 解方程组 ${\begin{array}{l} 2 x + 3 y = 7 \\ 3 x + 2 y = 8 \end{array}$

查看试题解析
19. 已知 $x = \sqrt{3} + 1, y = \sqrt{3} - 1$ ，求代数式 $x^{2} - 3 x y + y^{2}$ 的值．

查看试题解析
20. 如图，已知A(0，4)，B(－4，1)，C(3，0)．

(1)、写出△ABC关于x轴对称的△A₁B₁C₁的点A₁ ， B₁ ， C₁的坐标；

(2)、求△A₁B₁C₁的面积．

查看试题解析
21. 某校260名学生参加植树活动，要求每人植树4~7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2），经确认扇形图是正确的，而条形图尚有一处不符合题意．

回答下列问题：

(1)、写出条形图中存在的不符合题意，并说明理由；

(2)、写出这20名学生每人植树量的众数和中位数；

(3)、求这20名学生每人植树量的平均数，并估计这260名学生共植树多少棵？

查看试题解析
22. 如图，有三个论断：①∠1=∠2；②∠B=∠C；③∠A=∠D，请你从中任选两个作为条件，另一个作为结论构成一个命题，并证明该命题的正确性．

查看试题解析
23. 某校为奖励该校在南山区第二届学生技能大赛中表现突出的20名同学，派李老师为这些同学购买奖品，要求每人一件，李老师到文具店看了商品后，决定奖品在钢笔和笔记本中选择．如果买4个笔记本和2支钢笔，则需86元；如果买3个笔记本和1支钢笔，则需57元．

(1)、求笔记本和钢笔的单价分别为多少元？

(2)、售货员提示，购买笔记本没有优惠：买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受8折优惠，若买x（x＞10）支钢笔，所需费用为y元，请你求出y与x之间的函数关系式；

(3)、在（2）的条件下，如果买同一种奖品，请你帮忙计算说明，买哪种奖品费用更低．

查看试题解析
24. 小张骑自行车匀速从甲地到乙地，在途中因故停留了一段时间后，仍按原速骑行，小李骑摩托车比小张晚出发一段时间，以800米/分的速度匀速从乙地到甲地，两人距离乙地的路程y（米）与小张出发后的时间x（分）之间的函数图象如图所示.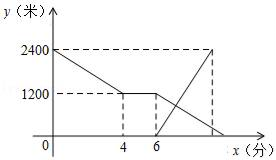

(1)、求小张骑自行车的速度；

(2)、求小张停留后再出发时y与x之间的函数表达式；

(3)、求小张与小李相遇时x的值.

查看试题解析
25. 建立模型：如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．
实践操作：过点A作AD⊥l于点D，过点B作BE⊥l于点E，求证：△CAD≌△BCE．

(1)、模型应用：如图2，在直角坐标系中，直线l₁：y= $\frac{4}{3}$ x+4与y轴交于点A，与x轴交于点B，将直线l₁绕着点A顺时针旋转45°得到l₂ ．求l₂的函数表达式．

(2)、如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．

查看试题解析