福建省泉州市惠安县2019-2020学年八年级上学期数学期末试卷
试卷更新日期：2020-11-24 类型：期末考试
一、单选题
-
1. 立方根是－3的数是（ ）．A、9 B、－27 C、－9 D、272. 下列运算正确的是（ ）．A、(－a)2 ． (－a)3=a6 B、(a2)3 a6= a12 C、a10÷a2=a5 D、a2+a3= a53. 下列六个数：0、 、 、 、－ 、 中，无理数出现的频数是（ ）.A、3 B、4 C、5 D、64. 如图，已知△ABC≌△DAE，BC=2，DE=5，则CE的长为（ ）
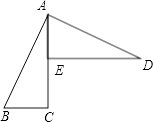A、2 B、2.5 C、3 D、3.55. 若等腰△ABC的周长为20，AB=8，则该等腰三角形的腰长为（ ）．A、8 B、6 C、4 D、8或66. 直线l上有三个正方形A、B、C放置如图所示，若正方形A、C的面积分别为1和12，则正方形B的面积为（ ）．
A、11 B、12 C、13 D、7. 用反证法证明命题：“在△ABC中，∠A、∠B对边分别是a、b ， 若∠A>∠B ， 则a>b”时第一步应假设（ ）．A、a < b B、a = b C、a ≥ b D、a ≤ b8. 已知实数a、b满足等式x=a2+b2+20，y=a(2b－a)，则x、y的大小关系是（ ）．A、x ≤ y B、x ≥ y C、x < y D、x > y9. 如图，等腰直角△ABC中，AC=BC ， BE平分∠ABC ， AD⊥BE的延长线于点D ， 若AD=2，则△ABE的面积为（ ）．
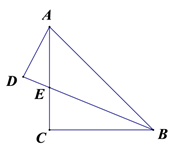A、4 B、6 C、2 D、210. 如图，透明的圆柱形玻璃容器(容器厚度忽略不计)的高为12cm ， 在容器内壁离容器底部4 cm 的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，且离容器上沿4 cm的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为15 cm ， 则该圆柱底面周长为（ ）cm ．
A、9 B、10 C、18 D、20二、填空题
-
11. 因式分解： .12. 计算(2x)3÷2x的结果为 ．13. 计算（x－a）（x+3）的结果中不含x的一次项，则a的值是.14. 我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ， 若k=2，则该等腰三角形的底角为 ．15. 某住宅小区有一块草坪如图所示，已知AB=6米，BC=8米，CD=24米，DA=26米，且AB⊥BC ， 则这块草坪的面积是平方米．
16. 如图， 在 的同侧， ，点 为 的中点，若 ，则 的最大值是 ．
三、解答题
-
17. 已知a是2的相反数，计算|a一2|的值．18. 先化简，再求值：2a·3a－(2a+3)(2a－3)，其中a=－2．19. 如图，已知AB=AC ， 点D、E在BC上，且∠ADE=∠AED ，
求证：BD=CE ．
20. 如图，△ABC中，AB=AC ． 按要求解答下面问题：
(1)、尺规作图：(保留作图痕迹，并把作图痕迹用黑色签字笔描黑)①作∠BAC的平分线AD交BC于点D；
②作边AB的垂直平分线EF ， EF与AD相交于点P；
③连结PB、PC ．
(2)、根据（1）中作出的符合题意图形，写出三条线段PA、PB、PC之间的数量关系．21. 如图，已知长方形纸片ABCD中，AB=10，AD=8，点E在AD边上，将△ABE沿BE折叠后，点A正好落在CD边上的点F处．
(1)、求DF的长；(2)、求△BEF的面积．22. 如果一个三角形的所有顶点都在网格的格点上，那么这个三角形叫做格点三角形，请在下列给定网格中按要求解答下面问题：
(1)、直接写出图1方格图(每个小方格边长均为1)中格点△ABC的面积；(2)、已知△A1B1C1三边长分别为 、 、 ，在图2方格图(每个小方格边长均为1)中画出格点△A1B1C1；(3)、已知△A2B2C2三边长分别为 、 、 (m>0，n>0，且m≠n)在图3所示4n×3m网格中画出格点△A2B2C2 ， 并求其面积．23. 参加学校运动会，八年级1班第一天购买了水果，面包，饮料，药品等四种食品，四种食品购买金额的统计图表如图1、图2所示，若将水果、面包、药品三种食品统称为非饮料食品，并规定t=饮料金额：非饮料金额．
(1)、①求t的值；②求扇形统计图中钝角∠AOB的度数
(2)、根据实际需要，该班第二天购买这四种食品时，增加购买饮料金额，同时减少购买面包金额假设增加购买饮料金额的25%等于减少购买面包的金额，且购买面包的金额不少于100元，求t的取值范围24. 如图，△ABC和△ADE中，AB=AD ， BC=DE ， ∠B=∠D ， 边AD与边BC交于点P(不与点B、C重合)，点B、E在AD异侧，I为△APC的内心(三条角平线的交点) ．
(1)、求证：∠BAD=∠CAE；(2)、当∠BAC=90°时，①若AB=16，BC=20时，求线段PD的最大值；
②若∠B=36°，∠AIC的取值范围为m°<∠AIC<n°，求m、n的值．
25. 如图，正方形ABCD的边长为a ， 射线AM是∠A外角的平分线，点E在边AB上运动(不与点A、B重合)，点F在射线AM上，且AF=√2BE ， CF与AD相交于点G ， 连结EC、EF、EG ．
(1)、求证：CE=EF；(2)、求△AEG的周长(用含a的代数式表示)(3)、试探索：点E在边AB上运动至什么位置时，△EAF的面积最大?