福建省南平市浦城县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 的值是( )A、0 B、1 C、 D、以上都不是2. 下列四个图案中,不是轴对称图案的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、a2•a3=a6 B、5a﹣2a=3a2 C、(a3)4=a12 D、(x+y)2=x2+y24. 若a、b、c为△ABC的三边长,且满足|a﹣4|+ =0,则c的值可以为( )A、5 B、6 C、7 D、85. 将分式 中的x,y的值同时扩大为原来的3倍,则分式的值( )A、扩大6倍 B、扩大9倍 C、不变 D、扩大3倍6. 石墨烯是现在世界上最薄的纳米材料,其理论厚度仅是0.00000000034m,这个数用科学记数法表示正确的是( )A、3.4×10-9m B、0.34×10-9m C、3.4×10-10m D、3.4×10-11m7. 在直角坐标系中,点P(3,1)关于x轴对称点的坐标是( )A、(3,1) B、(﹣3,1) C、(3,﹣1) D、(﹣3,﹣1)8. 如图,△ABC与△A'B'C'关于直线L对称,∠A=50°,∠C'=30°,则∠B的度数为( )
3. 下列运算正确的是( )A、a2•a3=a6 B、5a﹣2a=3a2 C、(a3)4=a12 D、(x+y)2=x2+y24. 若a、b、c为△ABC的三边长,且满足|a﹣4|+ =0,则c的值可以为( )A、5 B、6 C、7 D、85. 将分式 中的x,y的值同时扩大为原来的3倍,则分式的值( )A、扩大6倍 B、扩大9倍 C、不变 D、扩大3倍6. 石墨烯是现在世界上最薄的纳米材料,其理论厚度仅是0.00000000034m,这个数用科学记数法表示正确的是( )A、3.4×10-9m B、0.34×10-9m C、3.4×10-10m D、3.4×10-11m7. 在直角坐标系中,点P(3,1)关于x轴对称点的坐标是( )A、(3,1) B、(﹣3,1) C、(3,﹣1) D、(﹣3,﹣1)8. 如图,△ABC与△A'B'C'关于直线L对称,∠A=50°,∠C'=30°,则∠B的度数为( ) A、30° B、50° C、90° D、100°9. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )A、
A、30° B、50° C、90° D、100°9. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )A、 B、
B、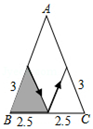 C、
C、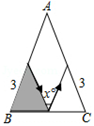 D、
D、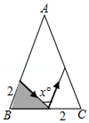 10. 现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
10. 现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )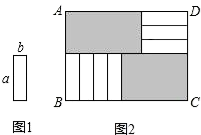 A、a=2b B、a=3b C、a=3.5b D、a=4b
A、a=2b B、a=3b C、a=3.5b D、a=4b二、填空题
-
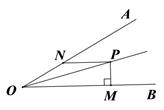
11. 当x 时,分式 无意义.12. 一个多边形的内角比四边形内角和多 ,并且这个多边形的各内角都相等,这个多边形的每个内角的度数是 .13. 分解因式:x2y﹣y= .14. 如图,∠AOB=30°,P是∠AOB的角平分线上的一点,PM⊥OB于点M,PN∥OB交OA于点N,若PM=1,则PN= .
 15. 工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.则过角尺顶点C的射线OC便是∠AOB的平分线。这样做的依据是.
15. 工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.则过角尺顶点C的射线OC便是∠AOB的平分线。这样做的依据是. 16. 等腰三角形ABC在平面直角坐标系中的位置如图所示,点A(﹣6,0),B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②,…,依此规律,第23次翻转后点C的横坐标是 .
16. 等腰三角形ABC在平面直角坐标系中的位置如图所示,点A(﹣6,0),B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②,…,依此规律,第23次翻转后点C的横坐标是 .
三、解答题
-
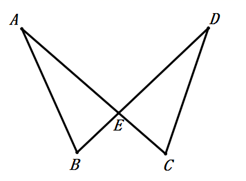
17. 如图,已知AB=DC,AC=BD,求证:∠B=∠C.
 18. 计算:[(x2+y2)﹣(x﹣y)2+2y(x﹣y)]÷4y.19. 解方程20. 如图所示,在 中, ,
18. 计算:[(x2+y2)﹣(x﹣y)2+2y(x﹣y)]÷4y.19. 解方程20. 如图所示,在 中, , (1)、用尺规在边BC上求作一点P,使 ;(不写作法,保留作图痕迹)(2)、连接AP当 为多少度时,AP平分 .21. 先化简,再求值:(1﹣ )÷ ,其中a=﹣3.22. 如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)、用尺规在边BC上求作一点P,使 ;(不写作法,保留作图痕迹)(2)、连接AP当 为多少度时,AP平分 .21. 先化简,再求值:(1﹣ )÷ ,其中a=﹣3.22. 如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB. (1)、若∠ABC=70°,则∠NMA的度数是度.(2)、若AB=8cm,△MBC的周长是14cm.
(1)、若∠ABC=70°,则∠NMA的度数是度.(2)、若AB=8cm,△MBC的周长是14cm.①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.
23. 为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
24. 在△ABC中,AB=AC.(1)、如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=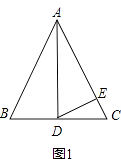 (2)、如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=
(2)、如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC= (3)、思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:(4)、如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
(3)、思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:(4)、如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由. 25. 在平面直角坐标系中,B(2,2 ),以OB为一边作等边△OAB(点A在x轴正半轴上).
25. 在平面直角坐标系中,B(2,2 ),以OB为一边作等边△OAB(点A在x轴正半轴上). (1)、若点C是y轴上任意一点,连接AC,在直线AC上方以AC为一边作等边△ACD.
(1)、若点C是y轴上任意一点,连接AC,在直线AC上方以AC为一边作等边△ACD.①如图1,当点D落在第二象限时,连接BD,求证:AB⊥BD;
②若△ABD是等腰三角形,求点C的坐标;
(2)、如图2,若FB是OA边上的中线,点M是FB一动点,点N是OB一动点,且OM+NM的值最小,请在图2中画出点M、N的位置,并求出OM+NM的最小值.