江西省宜春市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 在下列图形中,是中心对称图形而不是轴对称图形的是( )A、圆 B、等边三角形 C、梯形 D、平行四边形2. 下列事件中,必然事件是( )A、打开电视,正在播放宜春二套 B、抛一枚硬币,正面朝上 C、明天会下雨 D、地球绕着太阳转3. 若点 关于原点对称点 的坐标是 ,则 的值为( )A、 B、 C、 D、4. 关于 的一元二次方程 有实数根,则 满足( )A、 B、 且 C、 且 D、5. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、
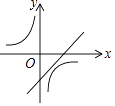 B、
B、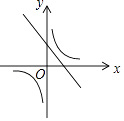 C、
C、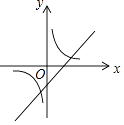 D、
D、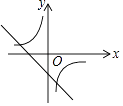 6. 已知二次函数 的图象如图所示,对于下列结论:① ;② ;③ ;④ ;⑤方程 的根是 , ,其中正确结论的个数是( )
6. 已知二次函数 的图象如图所示,对于下列结论:① ;② ;③ ;④ ;⑤方程 的根是 , ,其中正确结论的个数是( )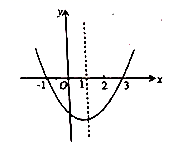 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
7. 将二次函数 化成 的形式,则y= .8. 已知函数 是反比例函数,则 的值为 .9. 若2是方程x2﹣2kx+3=0的一个根,则方程的另一根为 .10. 如图,四边形 是 的内接四边形,若 ,则 的大小为 .
 11. 在如图所示的网格中,每个小正方形的边长都为2,若以小正形的顶点为圆心,4为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为.
11. 在如图所示的网格中,每个小正方形的边长都为2,若以小正形的顶点为圆心,4为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为. 12. 如图,将函数 的图象沿 轴向下平移3个单位后交 轴于点 ,若点 是平移后函数图象上一点,且 的面积是3,已知点 ,则点 的坐标.
12. 如图,将函数 的图象沿 轴向下平移3个单位后交 轴于点 ,若点 是平移后函数图象上一点,且 的面积是3,已知点 ,则点 的坐标.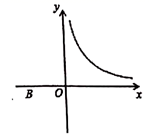
三、解答题
-
13.(1)、解方程:(2)、如图, 是等腰直角三角形, 是斜边,将 绕点 逆时针旋转后,能与 重合,如果 ,那么 的长等于多少?
 14. 已知抛物线(1)、抛物线经过原点时,求 的值;(2)、顶点在 轴上时,求 的值.15. 在一元二次方程x2-2ax+b=0中,若a2-b>0,则称a是该方程的中点值.(1)、方程x2-8x+3=0的中点值是;(2)、已知x2-mx+n=0的中点值是3,其中一个根是2,求mn的值.16. 如图,在矩形ABCD中,M是BC中点,请你仅用无刻度直尺按要求作图.
14. 已知抛物线(1)、抛物线经过原点时,求 的值;(2)、顶点在 轴上时,求 的值.15. 在一元二次方程x2-2ax+b=0中,若a2-b>0,则称a是该方程的中点值.(1)、方程x2-8x+3=0的中点值是;(2)、已知x2-mx+n=0的中点值是3,其中一个根是2,求mn的值.16. 如图,在矩形ABCD中,M是BC中点,请你仅用无刻度直尺按要求作图. (1)、在图1中,作AD的中点P;(2)、在图2中,作AB的中点Q.17. 元旦游园活动中,小文,小美,小红三位同学正在搬各自的椅子准备进行“抢凳子”游戏,看见李老师来了,小文立即邀请李老师参加,游戏规则如下:将三位同学的椅子背靠背放在教室中央,四人围着椅子绕圈行走,在行走过程中裁判员随机喊停,听到“停”后四人迅速抢坐在一张椅子上,没有抢坐到椅子的人淘汰,不能进入下一轮游戏.(1)、下列事件是必然事件的是( ) .A、李老师被淘汰 B、小文抢坐到自己带来的椅子 C、小红抢坐到小亮带来的椅子 D、有两位同学可以进入下一轮游戏(2)、如果李老师没有抢坐到任何一张椅子,三位同学都抢坐到了椅子但都没有抢坐到自己带来的椅子(记为事件 ),求出事件 的概率,请用树状图法或列表法加以说明.18. 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)、在图1中,作AD的中点P;(2)、在图2中,作AB的中点Q.17. 元旦游园活动中,小文,小美,小红三位同学正在搬各自的椅子准备进行“抢凳子”游戏,看见李老师来了,小文立即邀请李老师参加,游戏规则如下:将三位同学的椅子背靠背放在教室中央,四人围着椅子绕圈行走,在行走过程中裁判员随机喊停,听到“停”后四人迅速抢坐在一张椅子上,没有抢坐到椅子的人淘汰,不能进入下一轮游戏.(1)、下列事件是必然事件的是( ) .A、李老师被淘汰 B、小文抢坐到自己带来的椅子 C、小红抢坐到小亮带来的椅子 D、有两位同学可以进入下一轮游戏(2)、如果李老师没有抢坐到任何一张椅子,三位同学都抢坐到了椅子但都没有抢坐到自己带来的椅子(记为事件 ),求出事件 的概率,请用树状图法或列表法加以说明.18. 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.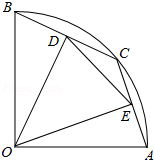 (1)、当BC=6时,求线段OD的长;(2)、在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.19. 某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
(1)、当BC=6时,求线段OD的长;(2)、在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.19. 某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:销售单价 (元/件)
…
30
40
50
60
…
每天销售量 (件)
…
500
400
300
200
…
(1)、研究发现,每天销售量 与单价 满足一次函数关系,求出 与 的关系式;(2)、当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?20. 如图,一次函数 ( 为常数,且 )的图像与反比例函数 的图像交于 , 两点. (1)、求一次函数的表达式;(2)、若将直线 向下平移 个单位长度后与反比例函数的图象有且只有一个公共点,求 的值.21. 如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)、求一次函数的表达式;(2)、若将直线 向下平移 个单位长度后与反比例函数的图象有且只有一个公共点,求 的值.21. 如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点. (1)、求该抛物线的解析式;(2)、求该抛物线的对称轴以及顶点坐标;(3)、设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.22. 如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)、求该抛物线的解析式;(2)、求该抛物线的对称轴以及顶点坐标;(3)、设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.22. 如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E (1)、判断直线PD是否为⊙O的切线,并说明理由;(2)、如果∠BED=60°,PD= ,求PA的长;(3)、将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.23. 如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)、判断直线PD是否为⊙O的切线,并说明理由;(2)、如果∠BED=60°,PD= ,求PA的长;(3)、将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.23. 如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形. (1)、试找出图1中的一个损矩形;(2)、试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;(3)、随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;(4)、在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.
(1)、试找出图1中的一个损矩形;(2)、试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;(3)、随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;(4)、在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.