江西省新余市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 在奔驰、宝马、丰田、三菱等汽车标志图形中,为中心对称图形的是( )
A、 B、
B、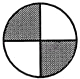 C、
C、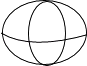 D、
D、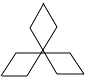 2. 已知关于x的一元二次方程3x2+4x﹣5=0,下列说法正确的是( )A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、没有实数根 D、无法确定3. 下列事件中,属于必然事件的是( )A、明天太阳从北边升起 B、实心铅球投入水中会下沉 C、篮球队员在罚球线投篮一次,投中 D、抛出一枚硬币,落地后正面向上4. 半径为10的⊙O和直线l上一点A,且OA=10,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相离 D、相切或相交5. 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
2. 已知关于x的一元二次方程3x2+4x﹣5=0,下列说法正确的是( )A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、没有实数根 D、无法确定3. 下列事件中,属于必然事件的是( )A、明天太阳从北边升起 B、实心铅球投入水中会下沉 C、篮球队员在罚球线投篮一次,投中 D、抛出一枚硬币,落地后正面向上4. 半径为10的⊙O和直线l上一点A,且OA=10,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相离 D、相切或相交5. 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( ) A、(-2,2 ) B、(-2,4) C、(-2,2 ) D、(2,2 )6. 如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y= (x>0)的图象上,则△OAB的面积等于( )
A、(-2,2 ) B、(-2,4) C、(-2,2 ) D、(2,2 )6. 如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y= (x>0)的图象上,则△OAB的面积等于( )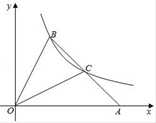 A、2 B、3 C、4 D、6
A、2 B、3 C、4 D、6二、填空题
-
7. 若反比例函数 的图象经过点 ,则 的值为.8. 在 中,给出以下4个条件:
⑴ ; ⑵ ;
⑶ ; ⑷ ;
从中任取一个条件,可以判定出 是直角三角形的概率是.
9. 如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是 cm,那么围成的圆锥的高度是cm. 10. 我们定义:关于x的函数y=ax2+bx与y=bx2+ax(其中a≠b)叫做互为交换函数.如y=3x2+4x与y=4x2+3x是互为交换函数.如果函数y=2x2+bx与它的交换函数图象顶点关于x轴对称,那么b= .11. 如图,在△ABC中,∠C=90°,AC=BC= ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B= .
10. 我们定义:关于x的函数y=ax2+bx与y=bx2+ax(其中a≠b)叫做互为交换函数.如y=3x2+4x与y=4x2+3x是互为交换函数.如果函数y=2x2+bx与它的交换函数图象顶点关于x轴对称,那么b= .11. 如图,在△ABC中,∠C=90°,AC=BC= ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B= . 12. 如图, 中, , , , 为 的中点,若动点 以 的速度从点 出发,沿着 的方向运动,设点 的运动时间为 秒 ,连接 ,当 是直角三角形时, 的值为秒.
12. 如图, 中, , , , 为 的中点,若动点 以 的速度从点 出发,沿着 的方向运动,设点 的运动时间为 秒 ,连接 ,当 是直角三角形时, 的值为秒.
三、解答题
-
13. 解方程(1)、 ;(2)、 .14. 如图,△ABC是⊙O的内接三角形,∠ABC=45°,请用无刻度的直尺按要求作图.
 (1)、如图1,请在图1中画出弦CD,使得CD=AC.(2)、如图2,AB是⊙O的直径,AN是⊙O的切线,点B,C,N在同一条直线上请在图中画出△ABN的边AN上的中线BD.15. 在一个不透明的袋子中装有三个完全相同的小球,分别标有数字2,3,4.从袋子中随机取出一个小球,用小球上的数字作为十位数字,然后放回,再取出一个小球,用小球上的数字作为个位数字,这样组成一个两位数,请用列表法或画树状图的方法完成下列问题.(1)、按这种方法组成两位数45是事件,填(“不可能”、“随机”、“必然”)(2)、组成的两位数能被3整除的概率是多少?16. 如图,在菱形 中, ,点 在对角线 上,将线段 绕点 顺时针旋转 ,得到 ,连接
(1)、如图1,请在图1中画出弦CD,使得CD=AC.(2)、如图2,AB是⊙O的直径,AN是⊙O的切线,点B,C,N在同一条直线上请在图中画出△ABN的边AN上的中线BD.15. 在一个不透明的袋子中装有三个完全相同的小球,分别标有数字2,3,4.从袋子中随机取出一个小球,用小球上的数字作为十位数字,然后放回,再取出一个小球,用小球上的数字作为个位数字,这样组成一个两位数,请用列表法或画树状图的方法完成下列问题.(1)、按这种方法组成两位数45是事件,填(“不可能”、“随机”、“必然”)(2)、组成的两位数能被3整除的概率是多少?16. 如图,在菱形 中, ,点 在对角线 上,将线段 绕点 顺时针旋转 ,得到 ,连接 (1)、求证: ;(2)、若 ,求四边形 的面积.17. 如图,平面直角坐标系中,以点A(2, )为圆心,以2为半径的圆与x轴交于B,C两点.若二次函数y=x2+bx+c的图象经过点B,C,试求此二次函数的顶点坐标.
(1)、求证: ;(2)、若 ,求四边形 的面积.17. 如图,平面直角坐标系中,以点A(2, )为圆心,以2为半径的圆与x轴交于B,C两点.若二次函数y=x2+bx+c的图象经过点B,C,试求此二次函数的顶点坐标. 18. 如图,已知反比例函数y= (x>0)的图象与一次函数y=﹣ x+4的图象交于A和B(6,n)两点.
18. 如图,已知反比例函数y= (x>0)的图象与一次函数y=﹣ x+4的图象交于A和B(6,n)两点.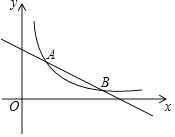 (1)、求k和n的值;
(1)、求k和n的值;
(2)、若点C(x,y)也在反比例函数y= (x>0)的图象上,求当2≤x≤6时,函数值y的取值范围.19. 已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,G是 上一点,AG与DC的延长线交于点F.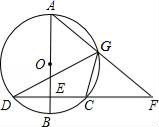 (1)、如CD=8,BE=2,求⊙O的半径长;(2)、求证:∠FGC=∠AGD.20. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量 (袋 与销售单价 (元 之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5.另外每天还需支付其他各项费用80元.
(1)、如CD=8,BE=2,求⊙O的半径长;(2)、求证:∠FGC=∠AGD.20. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量 (袋 与销售单价 (元 之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5.另外每天还需支付其他各项费用80元.销售单价 (元
3.5
5.5
销售量 (袋
280
120
(1)、请求出 与 之间的函数关系式;(2)、设每天的利润为 元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?21. 如图,在 中, ,点 在 上运动,点 在 上, 始终保持与 相等, 的垂直平分线交 于点 ,交 于 , (1)、判断 与 的位置关系,并说明理由;(2)、若 , , ,求线段 的长.22. 如果关于 的一元二次方程 ( )有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”,例如,方程 的两个根是2和4,则方程 就是“倍根方程”.(1)、若一元二次方程 是“倍根方程”,则 ;(2)、若 ( )是“倍根方程”,求代数式 的值;(3)、若方程 ( )是倍根方程,且相异两点 , ,都在抛物线 上,求一元二次方程 ( )的根.23. 如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)、判断 与 的位置关系,并说明理由;(2)、若 , , ,求线段 的长.22. 如果关于 的一元二次方程 ( )有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”,例如,方程 的两个根是2和4,则方程 就是“倍根方程”.(1)、若一元二次方程 是“倍根方程”,则 ;(2)、若 ( )是“倍根方程”,求代数式 的值;(3)、若方程 ( )是倍根方程,且相异两点 , ,都在抛物线 上,求一元二次方程 ( )的根.23. 如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).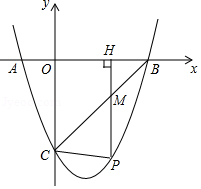 (1)、求这个二次函数的表达式;
(1)、求这个二次函数的表达式;
(2)、若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.