江西省萍乡市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 一元二次方程 的根是( )A、 B、 C、 D、2. 矩形、菱形、正方形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线互相平分且相等3. 已知 ,则下列各式不成立的是( )A、 B、 C、 D、4. 下列四个物体的俯视图与右边给出视图一致的是( )
 A、
A、 B、
B、 C、
C、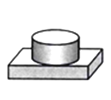 D、
D、 5. 已知点 、B(-1,y2)、C(3,y3)都在反比例函数 的图象上,则y1、y2、y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y36. 抛掷一枚质地均匀的硬币,连续掷三次,出现“一次正面,两次反面”的概率为( )A、 B、 C、 D、7. 如图所示,在矩形 中, ,点 在 边上, 平分 , ,垂足为 ,则 等于( )
5. 已知点 、B(-1,y2)、C(3,y3)都在反比例函数 的图象上,则y1、y2、y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y36. 抛掷一枚质地均匀的硬币,连续掷三次,出现“一次正面,两次反面”的概率为( )A、 B、 C、 D、7. 如图所示,在矩形 中, ,点 在 边上, 平分 , ,垂足为 ,则 等于( ) A、 B、1 C、 D、28. 如图,反比例函数 在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3.直线AB与x轴交于点C,则△AOC的面积为( )
A、 B、1 C、 D、28. 如图,反比例函数 在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3.直线AB与x轴交于点C,则△AOC的面积为( ) A、8 B、10 C、12 D、249. 某树主干长出若干数目的枝干,每个枝干又长出同样数目小分支,主干、枝干和小分支总数共57根,则主干长出枝干的根数为 ( )A、7 B、8 C、9 D、1010. 如图,在平行四边形 中, 为 的中点, 为 上一点, 交 于点 , ,则 的长为( )
A、8 B、10 C、12 D、249. 某树主干长出若干数目的枝干,每个枝干又长出同样数目小分支,主干、枝干和小分支总数共57根,则主干长出枝干的根数为 ( )A、7 B、8 C、9 D、1010. 如图,在平行四边形 中, 为 的中点, 为 上一点, 交 于点 , ,则 的长为( )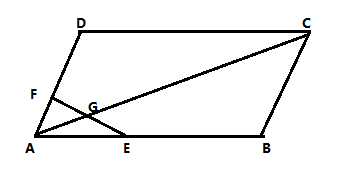 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一元二次方程x2﹣4x+4=0的解是 .
12. 在 中, , 为 的中点,则 的长为 .13. 四边形ABCD与四边形 位似,点O为位似中心.若 ,则 .14. 小英同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x,乙立方体朝上一面上的数字为y,这样就确定点P的一个坐标(x,y),那么点P落在双曲线y= 上的概率为 .15. 如图,身高为1.7m的小明AB站在小河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A、E、C′在一条线上.如果小河BD的宽度为12m,BE=3m,那么这棵树CD的高为m. 16. 如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数(k≠0,x>0)的图象过点B,E.若AB=2,则k的值为 .
16. 如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数(k≠0,x>0)的图象过点B,E.若AB=2,则k的值为 . 17. 关于 的一元二次方程 的二根为 ,且 ,则 .18. 如图,直角三角形 中, , , ,在线段 上取一点 ,作 交 于点 ,现将 沿 折叠,使点 落在线段 上,对应点记为 ; 的中点 的对应点记为 .若 ,则 .
17. 关于 的一元二次方程 的二根为 ,且 ,则 .18. 如图,直角三角形 中, , , ,在线段 上取一点 ,作 交 于点 ,现将 沿 折叠,使点 落在线段 上,对应点记为 ; 的中点 的对应点记为 .若 ,则 .
三、解答题
-
19.(1)、已知 ,求 的值;(2)、已知直线 分别截直线 于点 ,截直线 于点 ,且 , ,求 的长.
 20. 关于 的一元二次方程 .(1)、求证:此方程必有两个不相等的实数根;(2)、若方程有一根为1,求方程的另一根及 的值.21. 如图,是规格为8×8的正方形网格,请在所给的网格中按下列要求操作.
20. 关于 的一元二次方程 .(1)、求证:此方程必有两个不相等的实数根;(2)、若方程有一根为1,求方程的另一根及 的值.21. 如图,是规格为8×8的正方形网格,请在所给的网格中按下列要求操作. (1)、在网格中建立平面直角坐标系,使点 的坐标为 ,点 的坐标为 .(2)、在第二象限内的格点上画一点 ,使点 与线段 组成一个以 为底的等腰三角形,且腰长是无理数.求点 的坐标及 的周长(结果保留根号).(3)、将 绕点 顺时针旋转90°后得到 ,以点 为位似中心将 放大,使放大前后的位似比为1:2,画出放大后的 的图形.22. 如图,已知 ,直线 垂直平分 交 于 ,与边 交于 ,连接 ,过点 作 平行于 交 于点 ,连 .
(1)、在网格中建立平面直角坐标系,使点 的坐标为 ,点 的坐标为 .(2)、在第二象限内的格点上画一点 ,使点 与线段 组成一个以 为底的等腰三角形,且腰长是无理数.求点 的坐标及 的周长(结果保留根号).(3)、将 绕点 顺时针旋转90°后得到 ,以点 为位似中心将 放大,使放大前后的位似比为1:2,画出放大后的 的图形.22. 如图,已知 ,直线 垂直平分 交 于 ,与边 交于 ,连接 ,过点 作 平行于 交 于点 ,连 . (1)、求证: ;(2)、求证:四边形 是菱形;(3)、若 ,求菱形 的面积.23. 如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作一次函数表达式中的k,将B转盘指针指向的数字记作一次函数表达式中的b.
(1)、求证: ;(2)、求证:四边形 是菱形;(3)、若 ,求菱形 的面积.23. 如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作一次函数表达式中的k,将B转盘指针指向的数字记作一次函数表达式中的b. (1)、请用列表或画树状图的方法写出所有的可能;(2)、求一次函数y=kx+b的图象经过一、二、四象限的概率.24. 某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润为10元.调查表明:生产提高一个档次的蛋糕产品,该产品每件利润增加2元.
(1)、请用列表或画树状图的方法写出所有的可能;(2)、求一次函数y=kx+b的图象经过一、二、四象限的概率.24. 某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润为10元.调查表明:生产提高一个档次的蛋糕产品,该产品每件利润增加2元.
(1)、若生产的某批次蛋糕每件利润为14元,此批次蛋糕属于第几档次产品?
(2)、由于生产工序不同,蛋糕产品每提高一个档次,一天产量会减少4件.若生产的某档次产品一天的总利润为1080元,该烘焙店生产的是第几档次的产品?25. 如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB= , 反比例函数y=的图象的一支经过AO的中点C,且与AB交于点D. (1)、求反比例函数解析式(2)、若函数y=3x与y=的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比26. 如图①,矩形 中, , ,将 绕点 从 处开始按顺时针方向旋转, 交边 (或 )于点 , 交边 (或 )于点 .当 旋转至 处时, 的旋转随即停止.
(1)、求反比例函数解析式(2)、若函数y=3x与y=的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比26. 如图①,矩形 中, , ,将 绕点 从 处开始按顺时针方向旋转, 交边 (或 )于点 , 交边 (或 )于点 .当 旋转至 处时, 的旋转随即停止. (1)、特殊情形:如图②,发现当 过点 时, 也恰好过点 ,此时 是否与 相似?并说明理由;(2)、类比探究:如图③,在旋转过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由;(3)、拓展延伸:设 时, 的面积为 ,试用含 的代数式表示 ;
(1)、特殊情形:如图②,发现当 过点 时, 也恰好过点 ,此时 是否与 相似?并说明理由;(2)、类比探究:如图③,在旋转过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由;(3)、拓展延伸:设 时, 的面积为 ,试用含 的代数式表示 ;①在旋转过程中,若 时,求对应的 的面积;
②在旋转过程中,当 的面积为4.2时,求对应的 的值.