江西省南昌市2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各坐标表示的点在反比例函数 $y = \frac{4}{x}$ 图象上的是（）

A、 $(- 1, 4)$ B、 $(1, 4)$ C、 $(1, - 4)$ D、 $(2, - 2)$

查看试题解析
2. 下列各组图形中，一定相似的是（）

A、任意两个圆 B、任意两个等腰三角形 C、任意两个菱形 D、任意两个矩形

查看试题解析
3. 如图，在平面直角坐标系中，将 $Δ O A B$ 绕着旋转中心顺时针旋转 $90^{°}$ ，得到 $Δ C D E$ ，则旋转中心的坐标为（）

A、 $(1 ， 4)$ B、 $(1 ， 2)$ C、 $(1 ， 1)$ D、 $(- 1 ， 1)$

查看试题解析
4. 《九章算术》总共收集了246个数学问题，这些算法要比欧洲同类算法早1500多年，对中国及世界数学发展产生过重要影响. 在《九章算术》中有很多名题，下面就是其中的一道. 原文：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”翻译：如图， $C D$ 为 $⊙ O$ 的直径，弦 $A B ⊥ C D$ 于点 $E$ . $C E = 1$ 寸， $A B = 10$ 寸，则可得直径 $C D$ 的长为（）

A、13寸 B、26寸 C、18寸 D、24寸

查看试题解析
5. 已知 $x_{1}, x_{2}$ 是关于 $x$ 的一元二次方程 $x^{2} + k x - 1 = 0$ 的两个根，且满足 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = - 2$ ，则 $k$ 的值为（）

A、2 B、 $- 2$ C、1 D、 $- 1$

查看试题解析
6. 如图，在平面直角坐标系中，直线 $y = x + m (m > 0)$ 分别交 $x$ 轴， $y$ 轴于 $A ， B$ 两点，已知点 $C$ 的坐标为 $(- 2 ， 0)$ ，若 $D$ 为线段 $O B$ 的中点，连接 $A D ， D C$ ，且 $∠ A D C = ∠ O A B$ ，则 $m$ 的值是（）

A、12 B、6 C、8 D、4

查看试题解析

二、填空题

7. 反比例函数y＝ $\frac{m - 1}{x}$ 的图象在第一、三象限，则m的取值范围是．

查看试题解析
8. 如图，在 $□ A B C D$ 中，点 $E$ 在边 $C D$ 上，连接 $A E$ 并延长交 $B C$ 的延长线于点 $F$ ，若 $D E = 2 E C$ ，则 $B C ： C F =$ .

查看试题解析
9. 有三张除颜色外，大小、形状完全相同的卡片，第一张卡片两面都是红色，第二张卡片两面都是白色，第三张卡片一面是红色，一面是白色，用三只杯子分别把它们遮盖住，若任意移开其中的一只杯子，则看到的这张卡片两面都是红色的概率是.

查看试题解析
10. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ， $P$ 为 $\overset{⌢}{A B}$ 上一点，连接 $P A ， P E$ ，则 $∠ A P E$ 的度数为.

查看试题解析
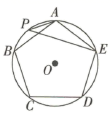11. 某市某楼盘的价格是每平方米6500元，由于市场萎靡，开发商为了加快资金周转，决定进行降价促销，经过连续两次下调后，该楼盘的价格为每平方米5265元. 设平均每次下调的百分率为 $x$ ，则可列方程为.

查看试题解析
12. 如图，抛物线 $y = \frac{1}{2} x^{2} + \frac{1}{2} x - 3$ 与 $x$ 轴的负半轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，连接 $A B$ ，点 $D ， E$ 分别是直线 $x = - 1$ 与抛物线上的点，若点 $A ， B ， D ， E$ 围成的四边形是平行四边形，则点 $E$ 的坐标为.

查看试题解析

三、解答题

13.

(1)、解方程： $x^{2} - 2 x - 24 = 0$ .

(2)、如图， $A ， B ， C ， D$ 四点都在 $⊙ O$ 上， $B D$ 为直径，四边形 $O A B C$ 是平行四边形，求 $∠ D$ 的度数.

查看试题解析
14. 如图，在 $Δ A B C$ 中， $D$ 是边 $A B$ 上的一点，若 $∠ A C D = ∠ B$ ，求证： $A C^{2} = A D \cdot A B$ .

查看试题解析
15. 如图，点 $A ， B ， C$ 都在 $⊙ O$ 上，请仅用无刻度的直尺分别按下列要求画图.（不写作法，保留作图痕迹）

(1)、在图1中，若 $∠ A B C = 45^{°}$ ，画一个 $⊙ O$ 的内接等腰直角三角形.

(2)、在图2中，若点 $D$ 在弦 $A C$ 上，且 $∠ A B D = 45^{°}$ ，画一个 $⊙ O$ 的内接等腰直角三角形.

查看试题解析
16. 已知布袋中有红、黄、蓝色小球各一个，用画树状图或列表的方法求下列事件的概率.

(1)、如果摸出第一个球后，不放回，再摸出第二球，求摸出的球颜色是“一黄一蓝”的概率.

(2)、随机从中摸出一个小球，记录下球的颜色后，把球放回，然后再摸出一个球，记录下球的颜色，求得到的球颜色是“一黄一蓝”的概率.

查看试题解析
17. 如图，反比例函数 $y = \frac{k}{x}$ 与一次函数 $y = a x + b$ 交于 $A (3 ， 1)$ 和 $B (- 1 ， m)$ 两点.

(1)、根据题中所给的条件，求出一次函数和反比例函数的解析式.

(2)、结合函数图象，指出当 $\frac{k}{x} > a x + b$ 时， $x$ 的取值范围.

查看试题解析
18. 如图， $O$ 为正方形 $A B C D$ 对角线上一点，以 $O$ 为圆心， $O A$ 长为半径的 $⊙ O$ 与 $B C$ 相切于点 $M$ .

(1)、求证： $C D$ 与 $⊙ O$ 相切.

(2)、若正方形 $A B C D$ 的边长为1，求半径 $O A$ 的长.

查看试题解析
19. 如图， $F$ 是 $Δ A B C$ 中 $A B$ 边上的中点， $F M / / A C$ 交 $B C$ 于点 $M$ ， $C$ 是 $Δ B D F$ 中 $B D$ 边上的中点，且 $A C$ 与 $D F$ 交于点 $E$ .

(1)、求 $\frac{E C}{A C}$ 的值.

(2)、若 $A B = m ， B F = C E$ ，求 $A C$ 的长.（用含 $m$ 的代数式表示）

查看试题解析
20. 如图， $Δ A O B$ 在平面直角坐标 $x O y$ 中，反比例函数 $y_{1} = \frac{k_{1}}{x}$ 的图象经过点 $A$ ，反比例函数 $y_{2} = \frac{k_{2}}{x}$ 的图象经过点 $B$ ，作直线 $x = 1$ 分别交 $y_{1} ， y_{2}$ 于 $C ， D$ 两点，已知 $A (2 ， 3) ， B (3 ， 1)$ .

(1)、求反比例函数 $y_{1} ， y_{2}$ 的解析式；

(2)、求 $Δ C O D$ 的面积.

查看试题解析
21. 如图，在 $Δ A B C$ 中， $∠ A C B = 90^{°} ， A B = 10 ， A C = 6$ ，正方形 $D E F G$ 的顶点 $D 、 G$ 分别在边 $A C$ 、 $B C$ 上， $E F$ 在边 $A B$ 上.

(1)、点 $C$ 到 $A B$ 的距离为.

(2)、求 $D E$ 的长.

查看试题解析
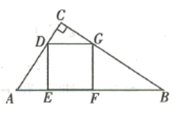22. 如图1，在矩形 $A B C D$ 中， $A D = 4 ， C D = 2$ ，点 $M$ 从点 $A$ 出发向点 $D$ 移动，速度为每秒1个单位长度，点 $N$ 从点 $C$ 出发向点 $D$ 移动，速度为每秒2个单位长度.两点同时出发，且其中的任何一点到达终点后，另一点的移动同时停止.

(1)、若两点的运动时间为 $t$ ，当 $t$ 为何值时， $Δ A M B \sim Δ D N A$ ？

(2)、在（1）的情况下，猜想 $A N$ 与 $B M$ 的位置关系并证明你的结论.

(3)、①如图2，当 $A B = C D = 2$ 时，其他条件不变，若（2）中的结论仍成立，则 $t =$ .
②当 $\frac{A D}{A B} = n (n > 1)$ ， $A B = 2$ 时，其他条件不变，若（2）中的结论仍成立，则 $t =$ （用含 $n$ 的代数式表示）.

查看试题解析
23. 定义：无论函数解析式中自变量的字母系数取何值，函数的图象都会过某一个点，这个点称为定点.例如，在函数 $y = k x$ 中，当 $x = 0$ 时，无论 $k$ 取何值，函数值 $y = 0$ ，所以这个函数的图象过定点 $(0 ， 0)$ .

(1)、求解体验
①关于 $x$ 的一次函数 $y = k x + 3 k (k \neq 0)$ 的图象过定点.

②关于 $x$ 的二次函数 $y = k x^{2} - k x + 2020 (k \neq 0)$ 的图象过定点和.

(2)、知识应用
若过原点的两条直线 $O A$ 、 $O B$ 分别与二次函数 $y = \frac{1}{2} x^{2}$ 交于点 $A (m ， \frac{1}{2} m^{2})$ 和点 $B (n ， \frac{1}{2} n^{2}) (m n < 0)$ 且 $O A ⊥ O B$ ，试求直线 $A B$ 所过的定点.

(3)、若直线 $C D ： y = k x + 2 k + 5$ 与拋物线 $y = x^{2}$ 交于 $C (c ， c^{2})$ 、 $D (d ， d^{2}) (c d < 0)$ 两点，试在拋物线 $y = x^{2}$ 上找一定点 $E$ ，使 $∠ C E D = 90 °$ ，求点 $E$ 的坐标.

查看试题解析