江西省吉安市吉州区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 下列方程中,关于x的一元二次方程是( )A、x2﹣x(x+3)=0 B、ax2+bx+c=0 C、x2﹣2x﹣3=0 D、x2﹣2y﹣1=02.
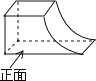
如图所示的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列说法正确的是( )A、一组对边相等且有一个角是直角的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线相等且互相垂直的四边形是正方形 D、对角线平分一组对角的平行四边形是菱形4. 如图, 在同一坐标系中(水平方向是x轴),函数 和 的图象大致是( )
3. 下列说法正确的是( )A、一组对边相等且有一个角是直角的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线相等且互相垂直的四边形是正方形 D、对角线平分一组对角的平行四边形是菱形4. 如图, 在同一坐标系中(水平方向是x轴),函数 和 的图象大致是( )
A、 B、
B、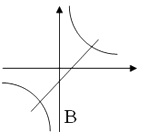 C、
C、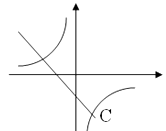 D、
D、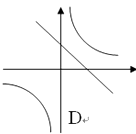 5. 若 = ,则 的值为( )A、5 B、 C、3 D、6. 如图,菱形ABCD的边长为6,∠ABC=120°,M是BC边的一个三等分点,P是对角线AC上的动点,当PB+PM的值最小时,PM的长是( )
5. 若 = ,则 的值为( )A、5 B、 C、3 D、6. 如图,菱形ABCD的边长为6,∠ABC=120°,M是BC边的一个三等分点,P是对角线AC上的动点,当PB+PM的值最小时,PM的长是( )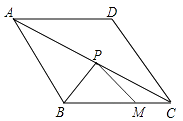 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 方程 的根是.8. 关于 的方程 有两个不相等的实数根,那么 的取值范围是 .9. 一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中约有红球个.
10. 设α,β是一元二次方程x2+3x﹣7=0的两个根,则α2+4α+β= .
11. 我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为步.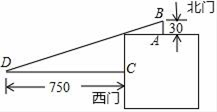 12. 如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 .
12. 如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 .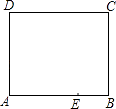
三、解答题
-
13. 解方程(1)、(2)、14. 为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.(1)、直接写出甲投放的垃圾恰好是A类的概率;(2)、求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.15.
一个直四棱柱的三视图如图所示,俯视图是一个菱形,求这个直四棱柱的表面积.
 16. 如图,在平行四边形 中,
16. 如图,在平行四边形 中, (1)、求 与 的周长之比;(2)、若 求 .17. 如图,是由两个等边三角形和一个正方形拼在-起的图形,请仅用无刻度的直尺按要求画图,
(1)、求 与 的周长之比;(2)、若 求 .17. 如图,是由两个等边三角形和一个正方形拼在-起的图形,请仅用无刻度的直尺按要求画图,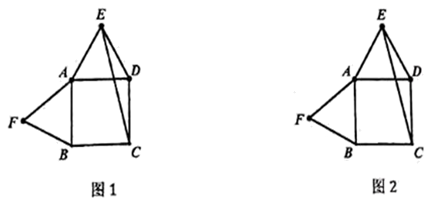 (1)、在图①中画一个 的角,使点 或点 是这个角的顶点,且以 为这个角的一边:(2)、在图②画一条直线 ,使得 .18. 某单位准备组织员工到武夷山风景区旅游,旅行社给出了如下收费标准(如图所示):
(1)、在图①中画一个 的角,使点 或点 是这个角的顶点,且以 为这个角的一边:(2)、在图②画一条直线 ,使得 .18. 某单位准备组织员工到武夷山风景区旅游,旅行社给出了如下收费标准(如图所示):
设参加旅游的员工人数为x人.
(1)、当25<x<40时,人均费用元,当x≥40时,人均费用为元;(2)、该单位共支付给旅行社旅游费用27000元,请问这次参加旅游的员工人数共有多少人?19. 如图,将▱ABCD的边AB延长至点E,使BE=AB,连接DE、EC、BD、DE交BC于点O. (1)、求证:△ABD≌△BEC;(2)、若∠BOD=2∠A,求证:四边形BECD是矩形.20. 如图1是一种折叠台灯,将其放置在水平桌面上,图2是其简化示意图,测得其灯臂 长为 灯翠 长为 ,底座 厚度为 根据使用习惯,灯臂 的倾斜角 固定为 ,
(1)、求证:△ABD≌△BEC;(2)、若∠BOD=2∠A,求证:四边形BECD是矩形.20. 如图1是一种折叠台灯,将其放置在水平桌面上,图2是其简化示意图,测得其灯臂 长为 灯翠 长为 ,底座 厚度为 根据使用习惯,灯臂 的倾斜角 固定为 , (1)、当 转动到与桌面平行时,求点 到桌面的距离;(2)、在使用过程中发现,当 转到至 时,光线效果最好,求此时灯罩顶端 到桌面的高度(参考数据: ,结果精确到个位).21. 如图,直线y=2x+6与反比例函数y= (k>0)的图像交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)、当 转动到与桌面平行时,求点 到桌面的距离;(2)、在使用过程中发现,当 转到至 时,光线效果最好,求此时灯罩顶端 到桌面的高度(参考数据: ,结果精确到个位).21. 如图,直线y=2x+6与反比例函数y= (k>0)的图像交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.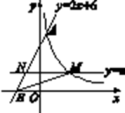 (1)、求m的值和反比例函数的表达式;(2)、直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?22. (问题情境)
(1)、求m的值和反比例函数的表达式;(2)、直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?22. (问题情境)如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
 (1)、(探究展示)
(1)、(探究展示)证明:AM=AD+MC;
(2)、AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.(3)、(拓展延伸)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
23. 定义:有一组邻边相等的凸四边形叫做“准菱形”,利用该定义完成以下各题: (1)、理解:如图1,在四边形ABCD中,若(填一种情况),则四边形ABCD是“准菱形”;(2)、应用:证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)(3)、拓展:如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.
(1)、理解:如图1,在四边形ABCD中,若(填一种情况),则四边形ABCD是“准菱形”;(2)、应用:证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)(3)、拓展:如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.