江西省吉安市吉安县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 如果某物体的三视图是如图所示的三个图形，

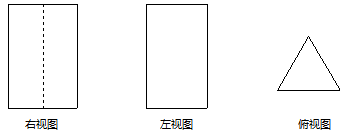
那么该物体的形状是（）

A、正方体 B、长方体 C、三棱柱 D、圆锥

查看试题解析
2. 下面四组线段中不能成比例线段的是（）

A、3、6、2、4 B、4、6、5、10 C、1、 $\sqrt{2}$ 、 $\sqrt{3}$ 、 $\sqrt{6}$ D、2 $\sqrt{5}$ 、 $\sqrt{15}$ 、4、2 $\sqrt{3}$

查看试题解析
3. 已知x²-2x=8，则3x²-6x-18的值为（）

A、54 B、6 C、-10 D、-18

查看试题解析
4. 顺次连接四边形ABCD各边的中点，所得四边形是（）

A、平行四边形 B、对角线互相垂直的四边形 C、矩形 D、菱形

查看试题解析
5. 在一个不透明的盒子中装有 $8$ 个白球,若于个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为 $\frac{2}{3}$ ,则黄球的个数为（）

A、 $2$ B、 $4$ C、 $12$ D、 $16$

查看试题解析
6. 两个相似多边形的面积比是9∶16，其中小多边形的周长为36 cm，则较大多边形的周长为（）

A、48 cm B、54 cm C、56 cm D、64 cm

查看试题解析
7. 如图，已知双曲线 $y = \frac{4}{x}$ 上有一点 $A$ ，过 $A$ 作 $A B$ 垂直 $x$ 轴于点 $B$ ，连接 $O A$ ，则 $Δ A O B$ 的面积为（）

A、 $1$ B、 $2$ C、 $4$ D、 $8$

查看试题解析
8. 如图，菱形ABCD与等边△AEF的边长相等，且E、F分别在BC、CD，则∠BAD的度数是（）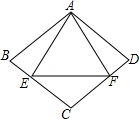

A、80° B、90° C、100° D、120°

查看试题解析

二、填空题

9. 写出一个以－1为一个根的一元二次方程．

查看试题解析
10. 反比例函数 $y = \frac{k + 2}{3 x}$ 的图象在一、三象限,则k应满足.

查看试题解析
11. 菱形有一个内角为60°，较短的对角线长为6，则它的面积为．

查看试题解析
12. 某养鱼专业户为了估计鱼塘中鱼的总条数，他先从鱼塘中捞出100条，将每条鱼作了记号后放回水中，当它们完全混合于鱼群后，再从鱼塘中捞出100条鱼，发现其中带记号的鱼有10条，估计该鱼塘里约有条鱼.

查看试题解析
13. 小华在距离路灯6米的地方，发现自己在地面上的影长是2米，若小华的身高为1.6米，那么路灯离地面的高度是米．

查看试题解析
14. 已知一元二次方程 $(a - 1) x^{2} + 7 a x + a^{2} + 3 a - 4 = 0$ 有一个根为0，则a的值为.

查看试题解析
15. 等腰三角形的底角为15°，腰长为20cm，则此三角形的面积为。

查看试题解析
16. 如图，矩形 $O A B C$ 的面积为 $\frac{100}{3}$ ，它的对角线 $O B$ 与双曲线 $y = \frac{k}{x}$ 相交于点 $D$ ，且 $O B ： O D = 5 ： 3$ ，则 $k =$ ．

查看试题解析

三、解答题

17. 解方程: ${(x + 1)}^{2} = 5 x + 5$ .

查看试题解析
18. 如图所示，折叠长方形一边AD，点D落在BC边的点F处，已知BC=10厘米，AB=8厘米，求FC的长．

查看试题解析
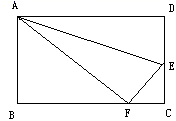19. 九年级1班将竞选出正、副班长各1名，现有甲、乙两位男生和丙、丁两位女生参加竞选．

(1)、男生当选班长的概率是；

(2)、请用列表或画树状图的方法求出两位女生同时当选正、副班长的概率．

查看试题解析
20. 已知一纸箱中放有大小均匀的x只白球和y只黄球，从箱中随机地取出一只白球的概率是 $\frac{2}{5}$ ．

(1)、写出y与x的函数关系式；

(2)、当x=10时，再往箱中放进20只白球，求随机地取出一只黄球的概率P．

查看试题解析
21. 如图，在正方形ABCD中，等边△AEF的顶点E、F分别在BC和CD上．

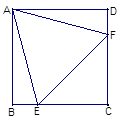(1)、求证：△ABE≌△ADF；

(2)、若等边△AEF的周长为6，求正方形ABCD的边长．

查看试题解析
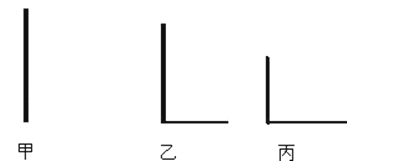
22.
三根垂直地面的木杆甲、乙、丙，在路灯下乙、丙的影子如图所示．试确定路灯灯泡的位置，再作出甲的影子．（不写作法，保留作图痕迹）

查看试题解析
23. 某商场销售一批名牌衬衫，平均每天可售出10件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出1件，若商场平均每天要盈利600元，每件衬衫应降价多少元？

查看试题解析
24. 如图，Rt△ABO的顶点A是双曲线 $y = \frac{k}{x}$ 与直线y=−x−(k+1)在第二象限的交点，AB⊥x轴于B且S_△ABO= $\frac{3}{2}$ 。

(1)、求这两个函数的解析式。

(2)、求直线与双曲线的两个交点A，C的坐标和△AOC的面积。

查看试题解析
25. 如图，在平面直角坐标系中，点 $B (12 ， 10)$ ，过点 $B$ 作 $x$ 轴的垂线，垂足为 $A$ .作 $y$ 轴的垂线，垂足为 $C$ 点 $D$ 从 $O$ 出发，沿 $y$ 轴正方向以每秒 $1$ 个单位长度运动；点 $E$ 从 $O$ 出发，沿 $x$ 轴正方向以每秒 $3$ 个单位长度运动；点 $F$ 从 $B$ 出发，沿 $B A$ 方向以每秒 $2$ 个单位长度运动.当 $E$ 点运动到点 $A$ 时，三点随之停止运动.设运动时间为 $t$ .

(1)、用含 $t$ 的代数式分别表示点 $E$ ，点 $F$ 的坐标.

(2)、若 $Δ O D E$ 与以点 $A$ ， $E$ ， $F$ 为顶点的三角形相似，求 $t$ 的值.

查看试题解析