江西省赣州市寻乌县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列哪个方程是一元二次方程（）

A、2x+y=1 B、x²+1=2xy C、x²+ $\frac{1}{x}$ =3 D、x²=2x﹣3

查看试题解析
2.
下列汽车标志中，是中心对称图形的有（）个．

A、1 B、2 C、3 D、4

查看试题解析
3. 如图，已知：在⊙O中，OA⊥BC，∠AOB=70°，则∠ADC的度数为（）

A、70° B、45° C、35° D、30°

查看试题解析
4. 如图，任意转动正六边形转盘一次，当转盘停止转动时，指针指向大于3的数的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
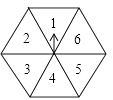5. 为了让江西的山更绿、水更清，2008年省委、省政府提出了确保到2010年实现全省森林覆盖率达到63%的目标，已知2008年我省森林覆盖率为60.05%，设从2008年起我省森林覆盖率的年平均增长率为 $x$ ，则可列方程（）

A、 $60.5 (1 + 2 x) = 63 %$ B、 $60.5 (1 + 2 x) = 63$ C、 $60.5 {(1 + x)}^{2} = 63 %$ D、 $60.5 {(1 + x)}^{2} = 63$

查看试题解析
6. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象如图，下列结论正确的是（）

A、 $a b c > 0$ B、若 $a x_{1}^{2} + b x_{1} = a x_{2}^{2} + b x_{2}$ 且 $x_{1} \neq x_{2}$ ，则 $x_{1} + x_{2} = 1$ C、 $a - b + c > 0$ D、当 $m \neq 1$ 时， $a + b > a m^{2} + b m$

查看试题解析

二、填空题

7. 若抛物线 $y = a x^{2} + b x + c$ 的开口向下，写出一个 $a$ 的可能值.

查看试题解析
8. 某十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是绿灯的概率为．

查看试题解析
9. 一元二次方程 $x^{2} - 4 x + 2 = 0$ 的两根为 $x_{1}$ , $x_{2}$ ,则 $x_{1}^{2} - 4 x_{1} + 2 x_{1} x_{2}$ 的值为 .

查看试题解析
10. 如图，在△ABC中，∠BAC＝33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB′C′，则∠B′AC的度数为．

查看试题解析
11. 如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为（4，2），点A的坐标为（2，0），则点B的坐标为．

查看试题解析
12. 平面内有四个点A、O、B、C，其中∠AOB=120⁰ ， ∠ACB=60⁰ ， AO=BO=2，则满足题意的OC长度为整数的值可以是．

查看试题解析

三、解答题

13.

(1)、解方程： $x (x - 2) + x - 2 = 0$

(2)、如图，四边形 $A B C D$ 是 $⊙ O$ 的内接四边形，若 $∠ B O D = 88 °$ ，求 $∠ B C D$ 的度数．

查看试题解析
14. 已知关于x的一元二次方程： $x^{2} - （ t-1 ） x + t - 2 = 0$ .

(1)、求证：对于任意实数t，方程都有实数根；

(2)、当t为何值时，方程的两个根互为相反数？请说明理由.

查看试题解析
15. 如图，△ABC的顶点都在方格线的交点（格点）上．

(1)、将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′，请在图中画出△A′B′C′；

(2)、将△ABC向上平移1个单位，再向右平移5个单位得到△A″B″C″，请在图中画出△A″B″C″；

(3)、若将△ABC绕原点O旋转180°，A的对应点A₁的坐标是．

查看试题解析
16. 如图，已知抛物线y=﹣x²+bx+c的图象经过（1，0），（0，3）两点．

(1)、求b，c的值；

(2)、写出当y＞0时，x的取值范围．

查看试题解析
17.
⊙O为△ABC的外接圆，请仅用无刻度的直尺，根据下列条件分别在图1，图2中画出一条弦，使这条弦将△ABC分成面积相等的两部分（保留作图痕迹，不写作法）．

(1)、如图1，AC=BC

(2)、如图2，直线l与⊙O相切于点P，且l∥BC。

查看试题解析
18. 有六张完全相同的卡片，分 $A ， B$ 两组，每组三张，在 $A$ 组的卡片上分别画上“√，×，√”， $B$ 组的卡片上分别画上“√，×，×”，如图①所示．

(1)、若将卡片无标记的一面朝上摆在桌上，再分别从两组卡片中随机各抽取一张，求两张卡片上标记都是“√”的概率（请用“树形图法”或“列表法”求解）．

(2)、若把 $A ， B$ 两组卡片无标记的一面对应粘贴在一起得到三张卡片，其正、反面标记如图②所示，将卡片正面朝上摆在桌上，并用瓶盖盖住标记．
①若随机揭开其中一个盖子，看到的标记是“√”的概率是多少？

②若揭开盖子，看到的卡片正面标记是“√”后，猜想它的反面也是“√”，求猜对的概率．

查看试题解析
19. 如图， $Rt △ A B C$ 中， $∠ A B C = 90 °$ ，以 $A B$ 为直径作半圆 $⊙ O$ 交 $A C$ 与点 $D$ ，点 $E$ 为 $B C$ 的中点，连结 $D E$ .

(1)、求证： $D E$ 是半圆 $⊙ O$ 的切线；

(2)、若 $∠ B A C = 30 °$ ， $D E = 2$ ，求 $A D$ 的长.

查看试题解析
20. 在Rt△ABC中，∠ACB=90°，AC=BC=3 $\sqrt{2}$ ，点D是斜边AB上一动点（点D与点A、B不重合），连接CD，将CD绕点C顺时针旋转90°得到CE，连接AE，DE．

(1)、求△ADE的周长的最小值；

(2)、若CD=4，求AE的长度．

查看试题解析
21. 某乡镇实施产业扶贫，帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节，已知该蜜柚的成本价为8元/千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销售量 $y$ (千克)与销售单价 $x$ (元/千克)之间的函数关系如图所示.

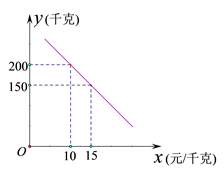(1)、求 $y$ 与 $x$ 的函数关系式，并写出 $x$ 的取值范围；

(2)、当该品种蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？

(3)、某农户今年共采摘蜜柚4800千克，该品种蜜柚的保质期为40天，根据(2)中获得最大利润的方式进行销售，能否销售完这批蜜柚？请说明理由.

查看试题解析
22. 如图，⊙O的半径为1，等腰直角三角形ABC的顶点B的坐标为（ $\sqrt{2}$ ，0），∠CAB=90°，AC=AB，顶点A在⊙O上运动．

(1)、当点A在x轴的正半轴上时，直接写出点C的坐标；

(2)、当点A运动到x轴的负半轴上时，试判断直线BC与⊙O位置关系，并说明理由；

(3)、设点A的横坐标为x，△ABC的面积为S，求S与x之间的函数关系式．

查看试题解析
23. 如图，已知二次函数 $L_{1} ： y = x^{2} - 4 x + 3$ 与 $x$ 轴交于 $A 、 B$ 两点（点 $A$ 在点 $B$ 的左边），与 $y$ 轴交于点 $C$ ．

(1)、写出 $A 、 B$ 两点的坐标；

(2)、二次函数 $L_{2} ： y = k x^{2} - 4 k x + 3 k (k \neq 0)$ ，顶点为 $P$ ．
①直接写出二次函数 $L_{2}$ 与二次函数 $L_{1}$ 有关图象的两条相同的性质；

②是否存在实数 $k$ ，使 $Δ A B P$ 为等边三角形？如存在，请求出 $k$ 的值；如不存在，请说明理由；

③若直线 $y = 8 k$ 与抛物线 $L_{2}$ 交于 $E 、 F$ 两点，问线段 $E F$ 的长度是否发生变化？如果不会，请求出 $E F$ 的长度；如果会，请说明理由．

查看试题解析