江西省赣州市兴国县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、摸出的是3个白球 B、摸出的是3个黑球 C、摸出的是2个白球、1个黑球 D、摸出的是2个黑球、1个白球3. 下列关于抛物线y=2x2﹣3的说法,正确的是( )A、抛物线的开口向下 B、抛物线的对称轴是直线x=1 C、抛物线与x轴有两个交点 D、抛物线y=2x2﹣3向左平移两个单位长度可得抛物线y=2(x﹣2)2﹣34. 反比例函数 在第一象限的图象如图所示,则k的值可能是( )
2. 不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、摸出的是3个白球 B、摸出的是3个黑球 C、摸出的是2个白球、1个黑球 D、摸出的是2个黑球、1个白球3. 下列关于抛物线y=2x2﹣3的说法,正确的是( )A、抛物线的开口向下 B、抛物线的对称轴是直线x=1 C、抛物线与x轴有两个交点 D、抛物线y=2x2﹣3向左平移两个单位长度可得抛物线y=2(x﹣2)2﹣34. 反比例函数 在第一象限的图象如图所示,则k的值可能是( )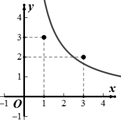 A、3 B、5 C、6 D、85. 如图,⊙O的弦AB⊥OC,且OD=2DC,AB= ,则⊙O的半径为( )
A、3 B、5 C、6 D、85. 如图,⊙O的弦AB⊥OC,且OD=2DC,AB= ,则⊙O的半径为( ) A、1 B、2 C、3 D、96. 国家实施“精准扶贫”政策以来,很多贫困人口走向了致富的道路.某地区2017年底有贫困人口25万人,通过社会各界的努力,2019年底贫困人口减少至9万人.设2017年底至2019年底该地区贫困人口的年平均下降率为x,根据题意可列方程( )A、25(1﹣2x)=9 B、 C、9(1+2x)=25 D、
A、1 B、2 C、3 D、96. 国家实施“精准扶贫”政策以来,很多贫困人口走向了致富的道路.某地区2017年底有贫困人口25万人,通过社会各界的努力,2019年底贫困人口减少至9万人.设2017年底至2019年底该地区贫困人口的年平均下降率为x,根据题意可列方程( )A、25(1﹣2x)=9 B、 C、9(1+2x)=25 D、二、填空题
-
7. 若函数y=(k-2) 是反比例函数,则k=.8. 已知:如图,△ABC的面积为16,点D、E分别是边AB、AC的中点,则△ADE的面积为 .
 9. 如图,已知圆锥的底面半径为3,高为4,则该圆锥的侧面积为 .
9. 如图,已知圆锥的底面半径为3,高为4,则该圆锥的侧面积为 .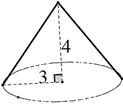 10. 如图,正六边形ABCDEF中的边长为6,点P为对角线BE上一动点,则PC的最小值为 .
10. 如图,正六边形ABCDEF中的边长为6,点P为对角线BE上一动点,则PC的最小值为 . 11.
11.如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为 cm.
 12. 在平面直角坐标系中,直线y=x-2与x轴、y轴分别交于点B、C,半径为1的⊙P的圆心P从点A(4,m )出发以每秒 个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t=秒时,⊙P与坐标轴相切.
12. 在平面直角坐标系中,直线y=x-2与x轴、y轴分别交于点B、C,半径为1的⊙P的圆心P从点A(4,m )出发以每秒 个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t=秒时,⊙P与坐标轴相切.
三、解答题
-
13.(1)、计算:(2)、解方程:14. 如图,AB∥CD,AC与BD交于点E,且AB=6,AE=4,AC=9.
 (1)、求CD的长;(2)、求证:△ABE∽△ACB.15. 已知 和 是关于x的一元二次方程 的两个不同的实数根.(1)、求k的取值范围;(2)、如果 且k为整数,求k的值.16. 如图, 是 内接三角形,点D是BC的中点,请仅用无刻度的直尺 , 分别按下列要求画图.
(1)、求CD的长;(2)、求证:△ABE∽△ACB.15. 已知 和 是关于x的一元二次方程 的两个不同的实数根.(1)、求k的取值范围;(2)、如果 且k为整数,求k的值.16. 如图, 是 内接三角形,点D是BC的中点,请仅用无刻度的直尺 , 分别按下列要求画图. (1)、如图1,画出弦AE,使AE平分∠BAC;(2)、如图2,∠BAF是 的一个外角,画出∠BAF的平分线.17. 2019年6月,习近平总书记对垃圾分类工作作出重要指示.实行垃圾分类,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.兴国县某校为培养学生垃圾分类的好习惯,在校园内摆放了几组垃圾桶,每组4个,分别是“可回收物”、“有害垃圾”、“厨余垃圾”和“其它垃圾”(如下图,分别记为A、B、C、D).小超同学由于上课没有听清楚老师的讲解,课后也没有认真学习教室里张贴的“垃圾分类常识”,对垃圾分类标准不是很清楚,于是先后将一个矿泉水瓶(简记为水瓶)和一张擦了汗的面巾纸(简记为纸巾)随机扔进了两个不同的垃圾桶。说明:矿泉水瓶属于“可回收物”,擦了汗的面巾纸属于“其它垃圾”.
(1)、如图1,画出弦AE,使AE平分∠BAC;(2)、如图2,∠BAF是 的一个外角,画出∠BAF的平分线.17. 2019年6月,习近平总书记对垃圾分类工作作出重要指示.实行垃圾分类,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.兴国县某校为培养学生垃圾分类的好习惯,在校园内摆放了几组垃圾桶,每组4个,分别是“可回收物”、“有害垃圾”、“厨余垃圾”和“其它垃圾”(如下图,分别记为A、B、C、D).小超同学由于上课没有听清楚老师的讲解,课后也没有认真学习教室里张贴的“垃圾分类常识”,对垃圾分类标准不是很清楚,于是先后将一个矿泉水瓶(简记为水瓶)和一张擦了汗的面巾纸(简记为纸巾)随机扔进了两个不同的垃圾桶。说明:矿泉水瓶属于“可回收物”,擦了汗的面巾纸属于“其它垃圾”. (1)、小超将矿泉水瓶随机扔进4个垃圾桶中的某一个桶,恰好分类正确的概率是;(2)、小超先后将一个矿泉水瓶和一张擦了汗的面巾纸随机扔进了两个不同的垃圾桶,请用画树状图或列表的方法,求出两个垃圾都分类错误的概率.18. 如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,﹣1).
(1)、小超将矿泉水瓶随机扔进4个垃圾桶中的某一个桶,恰好分类正确的概率是;(2)、小超先后将一个矿泉水瓶和一张擦了汗的面巾纸随机扔进了两个不同的垃圾桶,请用画树状图或列表的方法,求出两个垃圾都分类错误的概率.18. 如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,﹣1). (1)、以点C为中心,把△ABC逆时针旋转90°,请在图中画出旋转后的图形△A′B′C,点B′的坐标。(2)、在(1)的条件下,求出点A经过的路径 的长(结果保留π).19. 如图,AC是⊙O的直径,PA切⊙O于点A,PB切⊙O于点B,且∠APB=60°.
(1)、以点C为中心,把△ABC逆时针旋转90°,请在图中画出旋转后的图形△A′B′C,点B′的坐标。(2)、在(1)的条件下,求出点A经过的路径 的长(结果保留π).19. 如图,AC是⊙O的直径,PA切⊙O于点A,PB切⊙O于点B,且∠APB=60°. (1)、求∠BAC的度数;(2)、若PA= ,求点O到弦AB的距离.20. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .
(1)、求∠BAC的度数;(2)、若PA= ,求点O到弦AB的距离.20. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .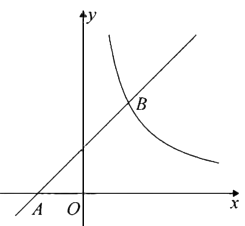 (1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
(1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
21. 一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:售价x(元/千克)
…
50
60
70
80
…
销售量y(千克)
…
100
90
80
70
…
(1)、求y与x的函数关系式;(2)、该批发商若想获得4000元的利润,应将售价定为多少元?(3)、该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?22. 如图,在 中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作 于点H,连接DE交线段OA于点F. (1)、试猜想直线DH与⊙O的位置关系,并说明理由;(2)、若AE=AH,EF=4,求DF的值.23. 如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.
(1)、试猜想直线DH与⊙O的位置关系,并说明理由;(2)、若AE=AH,EF=4,求DF的值.23. 如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m. (1)、求抛物线的解析式;(2)、若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;(3)、如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;(3)、如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.