江西省赣州市宁都县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 用配方法解方程x²﹣2x﹣5=0时，原方程应变形为（）

A、（x+1）²=6 B、（x+2）²=9 C、（x﹣1）²=6 D、（x﹣2）²=9

查看试题解析
2. 等腰三角形底角与顶角之间的函数关系是（）

A、正比例函数 B、一次函数 C、反比例函数 D、二次函数

查看试题解析
3. 如图，△ $A B O$ ∽△ $C D O$ ，若 $B O = 6$ ， $D O = 3$ ， $C D = 2$ ，则 $A B$ 的长是（）

A、2 B、3 C、4 D、5

查看试题解析
4. 下列事件中，必然事件是（）

A、抛掷 $1$ 个均匀的骰子，出现 $6$ 点向上 B、 $366$ 人中至少有 $2$ 人的生日相同 C、两直线被第三条直线所截，同位角相等 D、实数的绝对值是非负数

查看试题解析
5. 如图，⊙O中，弦BC与半径OA相交于点D，连接AB，OC．若∠A=60°，∠ADC=85°，则∠C的度数是（）

A、25° B、27.5° C、30° D、35°

查看试题解析
6. 如图，在平面直角坐标系中，菱形 $O A B C$ 的边 $O A$ 在 $x$ 轴的正半轴上，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过对角线 $O B$ 的中点 $D$ 和顶点 $C$ ．若菱形 $O A B C$ 的面积为12，则 $k$ 的值为（）．

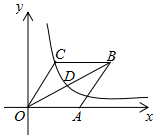A、6 B、5 C、4 D、3

查看试题解析

二、填空题

7. 抛物线 $y = 2 {(x - 3)}^{2} + 1$ 的顶点坐标是.

查看试题解析
8. 钟表分针的运动可看作是一种旋转现象，一只标准时钟的分针匀速旋转，经过15分钟旋转了度．

查看试题解析
9. 有4根细木棒，长度分别为2cm、3cm、4cm、5cm，从中任选3根，恰好能搭成一个三角形的概率是．

查看试题解析
10. 将三角形纸片（ $Δ A B C$ ）按如图所示的方式折叠，使点 $B$ 落在边 $A C$ 上，记为点 $B'$ ，折痕为 $E F$ ，已知 $A B = A C = 3$ ， $B C = 4$ ，若以点 $B'$ ， $F$ ， $C$ 为顶点的三角形与 $Δ A B C$ 相似，则 $B F$ 的长度是.

查看试题解析
11. 如图，已知菱形ABCD中，∠B=60°，点E在边BC上，∠BAE=25°，把线段AE绕点A逆时针方向旋转，使点E落在边CD上，那么旋转角 $α$ 的度数为．

查看试题解析
12. 已知直线y=kx（k≠0）经过点（12，﹣5），将直线向上平移m（m＞0）个单位，若平移后得到的直线与半径为6的⊙O相交（点O为坐标原点），则m的取值范围为．

查看试题解析
13. 进价为 $30$ 元/件的商品，当售价为 $40$ 元/件时，每天可销售 $40$ 件，售价每涨 $1$ 元，每天少销售 $1$ 件，当售价为元时每天销售该商品获得利润最大，最大利润是元．

查看试题解析

三、解答题

14. 解方程:

(1)、 $2 x^{2} + 1 = 3 x$

(2)、 ${(x - 3)}^{2} + 4 x (x - 3) = 0$

查看试题解析
15. 如图，在平行四边形 $A B C D$ 中，点 $E$ 在边 $D C$ 上， $D E ： E C = 3 ： 1$ ，连接 $A E$ 交 $B D$ 于点 $F$ ，则 $△ D E F$ 的面积与 $△ B A F$ 的面积之比为多少？

查看试题解析
16. 已知关于x的一元二次方程： $x^{2} - （ t-1 ） x + t - 2 = 0$ .

(1)、求证：对于任意实数t，方程都有实数根；

(2)、当t为何值时，方程的两个根互为相反数？请说明理由.

查看试题解析
17. 在 $5 \times 3$ 的方格纸中， $△ ABC$ 的三个顶点都在格点上．

(1)、在图1中画出线段BD，使 $BD / / AC$ ，其中D是格点；

(2)、在图2中画出线段BE，使 $BE ⊥ AC$ ，其中E是格点．

查看试题解析
18. 如图，双曲线 $y = \frac{m}{x}$ 经过点P(2，1)，且与直线y＝kx﹣4(k＜0)有两个不同的交点.

(1)、求m的值.

(2)、求k的取值范围.

查看试题解析
19. 八年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”“戏剧”“散文”“其他”四个类型，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．
类别
频数（人数）
频率
小说

0.5
戏剧
4

散文
10
0.25
其他
6

合计

1
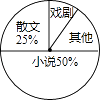
根据图表提供的信息，解答下列问题：

(1)、八年级一班有多少名学生？

(2)、请补全频数分布表，并求出扇形统计图中“其他”类所占的百分比；

(3)、在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组，请用画树状图或列表法的方法，求选取的2人恰好是乙和丙的概率．

查看试题解析
20. 如图， $A B$ 是 $⊙ O$ 的直径， $A C$ 是上半圆的弦，过点 $C$ 作 $⊙ O$ 的切线 $D E$ 交 $A B$ 的延长线于点 $E$ ，过点 $A$ 作切线 $D E$ 的垂线，垂足为 $D$ ，且与 $⊙ O$ 交于点 $F$ ，设 $∠ D A C$ ， $∠ C E A$ 的度数分别是 $a 、 β$ .

(1)、用含 $a$ 的代数式表示 $β$ ，并直接写出 $a$ 的取值范围；

(2)、连接 $O F$ 与 $A C$ 交于点 $O'$ ，当点 $O'$ 是 $A C$ 的中点时，求 $a 、 β$ 的值.

查看试题解析
21. 天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买A型和B型两行环保节能公交车共10辆，若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元，

(1)、求购买A型和B型公交车每辆各需多少万元？

(2)、预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1220万元，且确保这10辆公交车在该线路的年均载客量总和不少于650万人次，则该公司有哪几种购车方案？哪种购车方案总费用最少？最少总费用是多少？

查看试题解析
22. 如图，在等腰直角三角形ABC中， $∠ ACB = 90 ° ， AC = BC = 4$ D是AB的中点，E，F分别是AC，BC.上的点(点E不与端点A，C重合)，且 $AE = CF$ 连接EF并取EF的中点O，连接DO并延长至点G，使 $GO = OD$ ，连接DE，DF，GE，GF

(1)、求证：四边形EDFG是正方形；

(2)、直接写出当点E在什么位置时，四边形EDFG的面积最小?最小值是多少?

查看试题解析
23. 如图，在平面直角坐标系xOy中，抛物线 $y = a x^{2} - 2 a x - 3 a$ （ $a < 0$ ）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l： $y = k x + b$ 与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC.

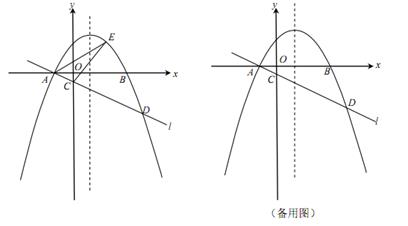(1)、直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；

(2)、点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为 $\frac{5}{4}$ ，求a的值；

(3)、设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由.

查看试题解析

类别	频数（人数）	频率
小说		0.5
戏剧	4
散文	10	0.25
其他	6
合计		1