江西省抚州市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 一元二次方程 的一根是1,则 的值是( )A、3 B、-3 C、2 D、-22. 把图1的正方体切下一个角,按图2放置,则切下的几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 华为手机锁屏密码是6位数,若密码的前4位数字已经知道,则一次解锁该手机密码的概率是( )A、 B、 C、 D、4. 如图,舞台纵深为6米,要想获得最佳音响效果,主持人应站在舞台纵深所在线段的离舞台前沿较近的黄金分割点 处,那么主持人站立的位置离舞台前沿较近的距离约为( )
3. 华为手机锁屏密码是6位数,若密码的前4位数字已经知道,则一次解锁该手机密码的概率是( )A、 B、 C、 D、4. 如图,舞台纵深为6米,要想获得最佳音响效果,主持人应站在舞台纵深所在线段的离舞台前沿较近的黄金分割点 处,那么主持人站立的位置离舞台前沿较近的距离约为( ) A、1.1米 B、1.5米 C、1.9米 D、2.3米5. 如图,矩形 的 边在 轴的正半轴上,点 的坐标为 ,反比例函数 的图象经过矩形对角线的交点 ,则 的值是( )
A、1.1米 B、1.5米 C、1.9米 D、2.3米5. 如图,矩形 的 边在 轴的正半轴上,点 的坐标为 ,反比例函数 的图象经过矩形对角线的交点 ,则 的值是( ) A、8 B、4 C、2 D、16. 如图,是抛物线 的图象,根据图象信息分析下列结论:① ;② ;③ ;④ .其中正确的结论是( )
A、8 B、4 C、2 D、16. 如图,是抛物线 的图象,根据图象信息分析下列结论:① ;② ;③ ;④ .其中正确的结论是( ) A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
7. 二次函数y=x2-2x+2图像的顶点坐标是 .8. 九年级8班第一小组 名同学在庆祝2020年新年之际,互送新年贺卡,表达同学间的真诚祝福,全组共送出贺卡30张,则x的值是 .9. 如图,在直角三角形 中, 是斜边 上的高, ,则 的值为.
 10. 如图,在菱形c中, 分别是边 ,对角线 与边 上的动点,连接 ,若 ,则 的最小值是 .
10. 如图,在菱形c中, 分别是边 ,对角线 与边 上的动点,连接 ,若 ,则 的最小值是 . 11. 如图,矩形 中, ,点 是边 上一点, 交 于点 ,则 长的取值范围是 .
11. 如图,矩形 中, ,点 是边 上一点, 交 于点 ,则 长的取值范围是 . 12. Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .
12. Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .三、解答题
-
13.(1)、 ;(2)、已知一个几何体的三视图如图所示,求该几何体的体积.
 14. 已知关于x的一元二次方程 的两实数根分别为 .(1)、求m的取值范围;(2)、若 ,求方程的两个根.15. 如图,平行四边形 中,点 是 的中点,用无刻度的直尺按下列要求作图.
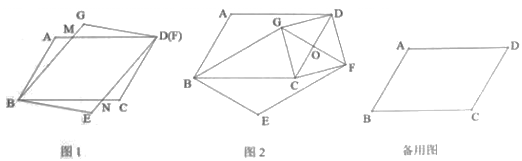
14. 已知关于x的一元二次方程 的两实数根分别为 .(1)、求m的取值范围;(2)、若 ,求方程的两个根.15. 如图,平行四边形 中,点 是 的中点,用无刻度的直尺按下列要求作图. (1)、在图1中,作边 上的中点 ;(2)、在图2中,作边 上的中点 .16. 垃圾分类是必须要落实的国家政策,环卫部门要求垃圾要按 可回收物, 有害垃圾, 餐厨垃圾, 其它垃圾四类分别装袋,投放.甲投放了一袋垃圾,乙投放了两袋垃圾(两袋垃圾不同类).(1)、直接写出甲投放的垃圾恰好是 类垃圾的概率;(2)、用树状图求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.17. 如图,在 中, , ,夹边 的长为6,求 的面积.
(1)、在图1中,作边 上的中点 ;(2)、在图2中,作边 上的中点 .16. 垃圾分类是必须要落实的国家政策,环卫部门要求垃圾要按 可回收物, 有害垃圾, 餐厨垃圾, 其它垃圾四类分别装袋,投放.甲投放了一袋垃圾,乙投放了两袋垃圾(两袋垃圾不同类).(1)、直接写出甲投放的垃圾恰好是 类垃圾的概率;(2)、用树状图求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.17. 如图,在 中, , ,夹边 的长为6,求 的面积. 18. 如图,反比例函数 的图象经过点 ,直线 与双曲线交于另一点 ,作 轴于点 , 轴于点 ,连接 .
18. 如图,反比例函数 的图象经过点 ,直线 与双曲线交于另一点 ,作 轴于点 , 轴于点 ,连接 . (1)、求 的值;(2)、若 ,求直线 的解析式;(3)、若 ,其它条件不变,直接写出 与 的位置关系.19. 2019年10月1日,是新中国70周年的生日,在首都北京天安门广场举行了盛大的建国70周年大阅兵,接受国家主席习近平的检阅,令国人振奋,令世界瞩目.在李克强总理庄严的指令下,56门礼炮,70响轰鸣,述说着56个民族,70载春华秋实的拼搏!图1是礼炮图片,图2是礼炮抽象示意图.已知: 是水平线, , , 的仰角分别是30°和10°, , ,且 .
(1)、求 的值;(2)、若 ,求直线 的解析式;(3)、若 ,其它条件不变,直接写出 与 的位置关系.19. 2019年10月1日,是新中国70周年的生日,在首都北京天安门广场举行了盛大的建国70周年大阅兵,接受国家主席习近平的检阅,令国人振奋,令世界瞩目.在李克强总理庄严的指令下,56门礼炮,70响轰鸣,述说着56个民族,70载春华秋实的拼搏!图1是礼炮图片,图2是礼炮抽象示意图.已知: 是水平线, , , 的仰角分别是30°和10°, , ,且 . (1)、求点 的铅直高度;(2)、求 两点的水平距离.
(1)、求点 的铅直高度;(2)、求 两点的水平距离.(结果精确到 ,参考数据: )
20. 某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于90%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)符合一次函数关系,如图所示: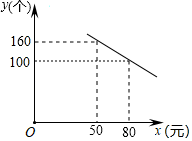 (1)、根据图象,直接写出y与x的函数关系式;(2)、该公司要想每天获得3000元的销售利润,销售单价应定为多少元(3)、销售单价为多少元时,每天获得的利润最大,最大利润是多少元?21. 如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G;
(1)、根据图象,直接写出y与x的函数关系式;(2)、该公司要想每天获得3000元的销售利润,销售单价应定为多少元(3)、销售单价为多少元时,每天获得的利润最大,最大利润是多少元?21. 如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G; (1)、求证:△ABE∽△EGB;(2)、若AB=4,求CG的长.
(1)、求证:△ABE∽△EGB;(2)、若AB=4,求CG的长.