福建省三明市2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-24 类型：期末考试

进入出卷网下载

一、单选题

1.
一个几何体的三视图如图所示，则这个几何体是（　　）

A、球体 B、圆锥 C、棱柱 D、圆柱

查看试题解析
2. 如图，AD∥BE∥CF，AB=3，BC=6，DE=2，则EF的值为（）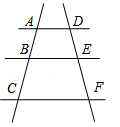

A、2 B、3 C、4 D、5

查看试题解析
3. 已知2x=3y ，则下列比例式成立的是（）

A、 $\frac{x}{2} = \frac{3}{y}$ B、 $\frac{x + y}{y} = \frac{4}{3}$ C、 $\frac{x}{3} = \frac{y}{2}$ D、 $\frac{x + y}{x} = \frac{3}{5}$

查看试题解析
4. 如图，在平面直角坐标系中，正方形OABC的顶点O、B的坐标分别是（0，0），（2，0），则顶点C的坐标是（）

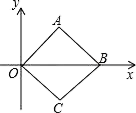A、（1，1） B、（﹣1，﹣1） C、（1，﹣1） D、（﹣1，1）

查看试题解析
5. 三角尺在灯泡O的照射下在墙上形成的影子如图所示，OA＝20cm，OA′＝50cm，则这个三角尺的周长与它在墙上形成的影子的周长的比是（）

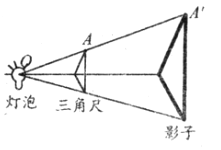A、5：2 B、2：5 C、4：25 D、25：4

查看试题解析
6. 在△ABC中，∠C＝90°．若AB＝3，BC＝1，则cosB的值为（）

A、 $\frac{1}{3}$ B、 $2 \sqrt{2}$ C、 $\frac{2 \sqrt{2}}{3}$ D、3

查看试题解析
7. 已知关于x的方程x²+3x+a=0有一个根为﹣2，则另一个根为（　　）

A、5 B、﹣1 C、2 D、﹣5

查看试题解析
8. 如图，在菱形ABCD中， $AE ⊥ BC$ 于E， $BE = EC$ ， $AC = 2$ ，则菱形ABCD的周长是 $($ $)$

A、5 B、10 C、8 D、12

查看试题解析
9. 如图，在矩形ABCD中，AD=10，AB=6，E为BC上一点，DE平分∠AEC，则CE的长为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图，一次函数y＝﹣x+3的图象与反比例函数y＝﹣ $\frac{4}{x}$ 的图象交于A，B两点，则不等式|﹣x+3|＞﹣ $\frac{4}{x}$ 的解集为（）

A、﹣1＜x＜0或x＞4 B、x＜﹣1或0＜x＜4 C、x＜﹣1或x＞0 D、x＜﹣1或x＞4

查看试题解析

二、填空题

11. 计算：sin30°＋tan45°＝．

查看试题解析
12. 若关于x的一元二次方程x²+2x+m﹣2＝0有实数根，则m的值可以是．（写出一个即可）

查看试题解析
13. 《算学宝鉴》中记载了我国数学家杨辉提出的一个问题：“直田积八百六十四步，之云阔不及长十二步，问长阔共几何?”译文：一个矩形田地的面积等于864平方步，且它的宽比长少12步，问长与宽的和是多少步?如果设矩形田地的长为x步，可列方程为．

查看试题解析
14. 在一个不透明的袋子中装有3个白球和若干个红球，这些球除颜色外都相同.每次从袋子中随机摸出一个球，记下颜色后再放回袋中，通过多次重复试验发现摸出红球的频率稳定在0.7附近，则袋子中红球约有个.

查看试题解析
15. 如图，已知点A，点C在反比例函数y＝ $\frac{k}{x}$ （k＞0，x＞0）的图象上，AB⊥x轴于点B，OC交AB于点D，若CD＝OD，则△AOD与△BCD的面积比为.

查看试题解析
16. 如图，在四边形ABCD中，∠DAB＝120°，∠DCB＝60°，CB＝CD，AC＝8，则四边形ABCD的面积为．

查看试题解析

三、解答题

17. 解方程：x²﹣2x﹣2=0．

查看试题解析
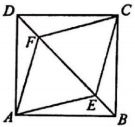
18. 树AB和木杆CD在同一时刻的投影如图所示，木杆CD高2m，影子DE长3m；若树的影子BE长7m，则树AB高多少m？

查看试题解析
19. 已知：如图， $E ， F$ 是正方形 $ABCD$ 的对角线 $BD$ 上的两点，且 $BE = DF$ .
求证：四边形 $AECF$ 是菱形.

查看试题解析
20. 如图所示是某路灯灯架示意图，其中点A表示电灯，AB和BC为灯架，l表示地面，已知AB＝2m，BC＝5.7m，∠ABC＝110°，BC⊥l于点C，求电灯A与地面l的距离．（结果精确到0.1m．参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）

查看试题解析
21. 如图，在矩形ABCD中，AB＝4，BC＝6，点M是BC的中点．

(1)、在AM上求作一点E，使△ADE∽△MAB（尺规作图，不写作法）；

(2)、在（1）的条件下，求AE的长．

查看试题解析
22. 习总书记指出“垃圾分类工作就是新时尚”．某小区为响应垃圾分类处理，改善生态环境，将生活垃圾分成三类：厨余垃圾、可回收垃圾和其他垃圾，分别记为a，b，c，并且设置了相应的垃圾箱：“厨余垃圾”箱、“可回收垃圾”箱和“其他垃圾”箱，分别记为A，B，C．

(1)、若小明将一袋分好类的生活垃圾随机投入一类垃圾箱，画树状图求垃圾投放正确的概率；

(2)、为了了解居民生活垃圾分类投放的情况，现随机抽取了小区某天三类垃圾箱中总共10吨的生活垃圾，数据统计如下（单位：吨）：

A

B

C

a

3

0.8

1.2

b

0.26

2.44

0.3

c

0.32

0.28

1.4

该小区所在的城市每天大约产生500吨生活垃圾，根据以上信息，试估算该城市生活垃圾中的“厨余垃圾”每月（按30天）有多少吨没有按要求投放．

查看试题解析
23. 某水果超市第一次花费2200元购进甲、乙两种水果共350千克．已知甲种水果进价每千克5元，售价每千克10元；乙种水果进价每千克8元，售价每千克12元．

(1)、第一次购进的甲、乙两种水果各多少千克？

(2)、由于第一次购进的水果很快销售完毕，超市决定再次购进甲、乙两种水果，它们的进价不变．若要本次购进的水果销售完毕后获得利润2090元，甲种水果进货量在第一次进货量的基础上增加了2m%，售价比第一次提高了m%；乙种水果的进货量为100千克，售价不变．求m的值．

查看试题解析
24. 如图，平面直角坐标系中，一次函数y＝x﹣1的图象与x轴，y轴分别交于点A，B，与反比例函数y＝ $\frac{k}{x}$ 的图象交于点C，D，CE⊥x轴于点E， $\frac{O A}{A E} = \frac{1}{3}$ ．

(1)、求反比例函数的表达式与点D的坐标；

(2)、以CE为边作▱ECMN，点M在一次函数y＝x﹣1的图象上，设点M的横坐标为a，当边MN与反比例函数y＝ $\frac{k}{x}$ 的图象有公共点时，求a的取值范围．

查看试题解析
25. 已知：在△EFG中，∠EFG＝90°，EF＝FG，且点E，F分别在矩形ABCD的边AB，AD上．

(1)、如图1，当点G在CD上时，求证：△AEF≌△DFG；

(2)、如图2，若F是AD的中点，FG与CD相交于点N，连接EN，求证：EN＝AE+DN；

(3)、如图3，若AE＝AD，EG，FG分别交CD于点M，N，求证：MG²＝MN•MD．

查看试题解析

	A	B	C
a	3	0.8	1.2
b	0.26	2.44	0.3
c	0.32	0.28	1.4