福建省泉州市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 若 有意义,则 的取值范围是( )A、 B、 C、 D、2. 若 ,则 ( )A、 B、 C、 D、3. 下列二次根式中,与 不是同类二次根式的是( )A、 B、 C、 D、4. 某快递公司2017年“双十一”与2019年“双十一”期间完成投递的件数分别为8万件和11万件.设该快递公司这两年投递件数的年平均增长率为 ,则下列方程正确的是( )A、 B、 C、 D、5. 如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的 ,则AO:AD的值为( )
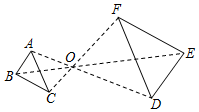 A、2:3 B、2:5 C、4:9 D、4:136. 利用配方法解一元二次方程 时,将方程配方为 ,则 、 的值分别为( )A、 , B、 , C、 , D、 ,7. 如图为某一试验结果的频率随试验次数变化趋势图,则下列试验中不符合该图的是( )
A、2:3 B、2:5 C、4:9 D、4:136. 利用配方法解一元二次方程 时,将方程配方为 ,则 、 的值分别为( )A、 , B、 , C、 , D、 ,7. 如图为某一试验结果的频率随试验次数变化趋势图,则下列试验中不符合该图的是( )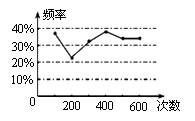 A、掷一枚普通正六面体骰子,出现点数不超过2 B、掷一枚硬币,出现正面朝上 C、从装有2个黑球、1个白球的不透明布袋中随机摸出一球为白球 D、从分别标有数字l,2,3,4,5,6,7,8,9的九张卡片中,随机抽取一张卡片所标记的数字不小于78. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据某地的地理位置设计的圭表,其中,立柱 高为 .已知冬至时某地的正午日光入射角 约为 ,则立柱根部与圭表的冬至线的距离(即 的长)约为( )
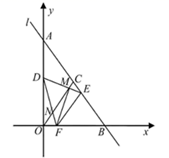
A、掷一枚普通正六面体骰子,出现点数不超过2 B、掷一枚硬币,出现正面朝上 C、从装有2个黑球、1个白球的不透明布袋中随机摸出一球为白球 D、从分别标有数字l,2,3,4,5,6,7,8,9的九张卡片中,随机抽取一张卡片所标记的数字不小于78. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据某地的地理位置设计的圭表,其中,立柱 高为 .已知冬至时某地的正午日光入射角 约为 ,则立柱根部与圭表的冬至线的距离(即 的长)约为( )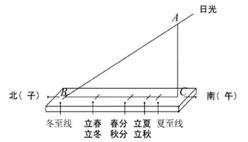 A、 B、 C、 D、9. 如图,在 中,对角线 与 相交于点 ,点 是 的中点, 与 相交于点 ,则 的值为( )
A、 B、 C、 D、9. 如图,在 中,对角线 与 相交于点 ,点 是 的中点, 与 相交于点 ,则 的值为( )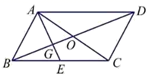 A、 B、 C、 D、10. 已知实数 是一元二次方程 的根,则 的值为( )A、48 B、49 C、50 D、51
A、 B、 C、 D、10. 已知实数 是一元二次方程 的根,则 的值为( )A、48 B、49 C、50 D、51二、填空题
-
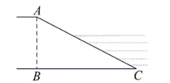
11. 计算: .12. 一元二次方程 的根是 .13. 如图,河堤横断面迎水坡 的坡度 ,若 米,则高度 为米.
 14. 如图,在 中, , , , 、 分别是 与 的中点,则 的长为 .
14. 如图,在 中, , , , 、 分别是 与 的中点,则 的长为 . 15. 如图,在正方形网格中, 的三个顶点都在格点上,则 .
15. 如图,在正方形网格中, 的三个顶点都在格点上,则 . 16. 在正方形 中, ,点 在边 上,作点 关于 的对称点 ,连接 并延长交 于点 ,若点 将 分为 的两部分,则 .
16. 在正方形 中, ,点 在边 上,作点 关于 的对称点 ,连接 并延长交 于点 ,若点 将 分为 的两部分,则 .三、解答题
-
17. 计算: .18. 已知关于 的一元二次方程 的两根分别为 、 ,有如下结论: , .试利用上述结论,解决问题:
已知关于 的一元二次方程 的两根分别为 、 ,求 的值.
19. 某校有一块矩形绿地(数据如图所示,单位: ),现在其中修建一条道路(阴影所示),若所修建道路的面积为 ,求 的值.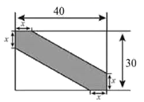 20. 已知关于 的一元二次方程 .(1)、求证:这个方程一定有实根;(2)、若这个方程有一根为-3,试求 的值.21. 如图,在矩形 中, .
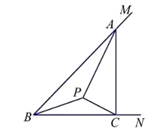
20. 已知关于 的一元二次方程 .(1)、求证:这个方程一定有实根;(2)、若这个方程有一根为-3,试求 的值.21. 如图,在矩形 中, . (1)、尺规作图:在线段 上求作一点 ,使得 ,(保留作图痕迹,不写作法与证明);(2)、连接 ,若点 为边 的中点,求证: .22. 将一副直角三角尺按如图所示方式放置,点 、 、 在同一条直线上, , , , , , ,求 的长.
(1)、尺规作图:在线段 上求作一点 ,使得 ,(保留作图痕迹,不写作法与证明);(2)、连接 ,若点 为边 的中点,求证: .22. 将一副直角三角尺按如图所示方式放置,点 、 、 在同一条直线上, , , , , , ,求 的长.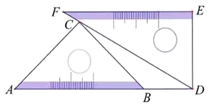 23. 某台机床生产铸件产品,按照生产标准,铸件产品评定等级、整改费用规定如下:
23. 某台机床生产铸件产品,按照生产标准,铸件产品评定等级、整改费用规定如下:重量
(单位: ,精确到0.1)
评定等级
整改费用
(单位:元/件)
特优品
优等品
合格品
不合格品
50
不合格品
30
注:在统计优等品个数时,将特优品计算在内;在统计合格品个数时,将优等品(含特优品)计算在内.
现该机床生产20件产品,测量其重量,得到如下统计表:
重量
(单位: ,精确到0.1)
29.8
29.9
30.0
30.1
30.2
件数
2
3
4
3
1
对照生产标准,发现这批铸件产品的合格率为 .
(1)、求 与 的值;(2)、根据客户要求,这批铸件产品的合格率不得低于 .现决定从不合格产品中随机抽取两件进行整改,求整改费用最低的概率.