福建省宁德市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. sin30°等于( )A、 B、 C、 D、2. 已知一个几何体如图所示,则该几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 在一个不透明的袋子中放有若干个球,其中有6个白球,其余是红球,这些球除颜色外完全相同.每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0.25左右,则红球的个数约是( )A、2 B、12 C、18 D、244. 在Rt△ABC中,∠C=900 , AC=4,AB=5,则sinB的值是( )A、 B、 C、 D、5. 如图,四边形 与四边形 是位似图形,则位似中心是( )
3. 在一个不透明的袋子中放有若干个球,其中有6个白球,其余是红球,这些球除颜色外完全相同.每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0.25左右,则红球的个数约是( )A、2 B、12 C、18 D、244. 在Rt△ABC中,∠C=900 , AC=4,AB=5,则sinB的值是( )A、 B、 C、 D、5. 如图,四边形 与四边形 是位似图形,则位似中心是( ) A、点 B、点 C、点 D、点6. 如图,在四边形 中,对角线 , 相交于点 ,且 , .若要使四边形 为菱形,则可以添加的条件是( )
A、点 B、点 C、点 D、点6. 如图,在四边形 中,对角线 , 相交于点 ,且 , .若要使四边形 为菱形,则可以添加的条件是( ) A、 B、 C、 D、7. 对于反比例函数 ,下列说法正确的是( )A、 的值随 值的增大而增大 B、 的值随 值的增大而减小 C、当 时, 的值随 值的增大而增大 D、当 时, 的值随 值的增大而减小8. 若方程 有两个不相等的实数根,则实数 的值可能是( )A、3 B、4 C、5 D、69. 已知抛物线 经过点 , ,若 , 是关于 的一元二次方程 的两个根,且 , ,则下列结论一定正确的是( )A、 B、 C、 D、10. 如图,一根电线杆 垂直于地面,并用两根拉线 , 固定,量得 , ,则拉线 , 的长度之比 ( )
A、 B、 C、 D、7. 对于反比例函数 ,下列说法正确的是( )A、 的值随 值的增大而增大 B、 的值随 值的增大而减小 C、当 时, 的值随 值的增大而增大 D、当 时, 的值随 值的增大而减小8. 若方程 有两个不相等的实数根,则实数 的值可能是( )A、3 B、4 C、5 D、69. 已知抛物线 经过点 , ,若 , 是关于 的一元二次方程 的两个根,且 , ,则下列结论一定正确的是( )A、 B、 C、 D、10. 如图,一根电线杆 垂直于地面,并用两根拉线 , 固定,量得 , ,则拉线 , 的长度之比 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 ,则 .12. 已知一个几何体的主视图与俯视图如图所示,则该几何体可能是.
 13. 如图,公路 互相垂直,公路 的中点 与点 被湖隔开,若测得 的长为2.4km,则 两点间的距离为km.
13. 如图,公路 互相垂直,公路 的中点 与点 被湖隔开,若测得 的长为2.4km,则 两点间的距离为km. 14. 中国古代数学著作《九章算术》中记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文为:已知长方形门的高比宽多6.8尺,门的对角线长为10尺,那么门的高和宽各是多少尺?设长方形门的宽为 尺,则可列方程为.15. 如图, 分别为矩形 的边 , 的中点,若矩形 与矩形 相似,则相似比等于.
14. 中国古代数学著作《九章算术》中记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文为:已知长方形门的高比宽多6.8尺,门的对角线长为10尺,那么门的高和宽各是多少尺?设长方形门的宽为 尺,则可列方程为.15. 如图, 分别为矩形 的边 , 的中点,若矩形 与矩形 相似,则相似比等于.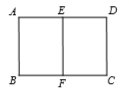 16. 如图,正方形的顶点 分别在 轴和 轴上,边 的中点 在 轴上,若反比例函数 的图象恰好经过 的中点 ,则 的长为 .
16. 如图,正方形的顶点 分别在 轴和 轴上,边 的中点 在 轴上,若反比例函数 的图象恰好经过 的中点 ,则 的长为 .
三、解答题
-
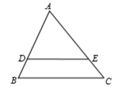
17. 解方程: .18. 如图, 分别是 的边 , 上的点, , , , ,求 的长.
 19. 如图,点 在 轴正半轴上,点 是反比例函数图象上的一点,且 .过点 作 轴交反比例函数图象于点 .
19. 如图,点 在 轴正半轴上,点 是反比例函数图象上的一点,且 .过点 作 轴交反比例函数图象于点 . (1)、求反比例函数的表达式;(2)、求点 的坐标.20. 如图,在菱形 中,点 在对角线 上,延长 交 于点 .
(1)、求反比例函数的表达式;(2)、求点 的坐标.20. 如图,在菱形 中,点 在对角线 上,延长 交 于点 . (1)、求证: ;(2)、已知点 在边 上,请以 为边,用尺规作一个 与 相似,并使得点 在 上.(只须作出一个 ,保留作图痕迹,不写作法)21. 某化肥厂2019年生产氮肥4000吨,现准备通过改进技术提升生产效率,计划到2021年生产氮肥4840吨.现技术攻关小组按要求给出甲、乙两种技术改进方案,其中运用甲方案能使每年产量增长的百分率相同,运用乙方案能使每年增长的产量相同.问运用哪一种方案能使2020年氮肥的产量更高?高多少?22. 某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子 ,点 恰好在水面中心,安装在柱子顶端 处的圆形喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过 的任意平面上,水流喷出的高度 与水平距离 之间的关系如图所示,建立平面直角坐标系,右边抛物线的关系式为 .请完成下列问题:
(1)、求证: ;(2)、已知点 在边 上,请以 为边,用尺规作一个 与 相似,并使得点 在 上.(只须作出一个 ,保留作图痕迹,不写作法)21. 某化肥厂2019年生产氮肥4000吨,现准备通过改进技术提升生产效率,计划到2021年生产氮肥4840吨.现技术攻关小组按要求给出甲、乙两种技术改进方案,其中运用甲方案能使每年产量增长的百分率相同,运用乙方案能使每年增长的产量相同.问运用哪一种方案能使2020年氮肥的产量更高?高多少?22. 某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子 ,点 恰好在水面中心,安装在柱子顶端 处的圆形喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过 的任意平面上,水流喷出的高度 与水平距离 之间的关系如图所示,建立平面直角坐标系,右边抛物线的关系式为 .请完成下列问题:
 (1)、将 化为 的形式,并写出喷出的水流距水平面的最大高度是多少米;(2)、写出左边那条抛物线的表达式;(3)、不计其他因素,若要使喷出的水流落在池内,水池的直径至少要多少米?23. 4月23日,为迎接“世界读书日”,某书城开展购书有奖活动.顾客每购书满100元获得一次摸奖机会,规则为:一个不透明的袋子中装有4个小球,小球上分别标有数字1,2,3,4,它们除所标数字外完全相同,摇匀后同时从中随机摸出两个小球,则两球所标数字之和与奖励的购书券金额的对应关系如下:
(1)、将 化为 的形式,并写出喷出的水流距水平面的最大高度是多少米;(2)、写出左边那条抛物线的表达式;(3)、不计其他因素,若要使喷出的水流落在池内,水池的直径至少要多少米?23. 4月23日,为迎接“世界读书日”,某书城开展购书有奖活动.顾客每购书满100元获得一次摸奖机会,规则为:一个不透明的袋子中装有4个小球,小球上分别标有数字1,2,3,4,它们除所标数字外完全相同,摇匀后同时从中随机摸出两个小球,则两球所标数字之和与奖励的购书券金额的对应关系如下:两球所标数字之和
3
4
5
6
7
奖励的购书券金额(元)
0
0
30
60
90
(1)、通过列表或画树状图的方法计算摸奖一次获得90元购书券的概率;(2)、书城规定:如果顾客不愿意参加摸奖,那么可以直接获得30元的购书券.在“参加摸奖”和“直接获得购书券”两种方式中,你认为哪种方式对顾客更合算?请通过求平均教的方法说明理由.
