福建省南平市2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个手机应用图标中是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 将抛物线y=x²向左平移2个单位，再向下平移1个单位，所得抛物线为（　　）

A、y=（x﹣2）²﹣1 B、y=（x﹣2）²+1 C、y=（x+2）²﹣1 D、y=（x+2）²+1

查看试题解析
3. 下列事件是必然事件的是（）

A、乘坐公共汽车恰好有空座 B、同位角相等 C、打开手机就有未接电话 D、三角形内角和等于180°

查看试题解析
4. 如图，点A，B，C在⊙O上，∠BOC＝60°，则∠BAC的度数是（）

A、15° B、30° C、45° D、20°

查看试题解析
5. 下列命题错误的是（）

A、经过三个点一定可以作圆 B、经过切点且垂直于切线的直线必经过圆心 C、同圆或等圆中，相等的圆心角所对的弧相等 D、三角形的外心到三角形各顶点的距离相等

查看试题解析
6. 已知正六边形的边长为2，则它的内切圆的半径为（）

A、1 B、 $\sqrt{3}$ C、2 $\sqrt{3}$ D、2

查看试题解析
7. 如图，PA、PB切⊙O于点A、B，PA=10，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长是（）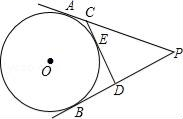

A、10 B、18 C、20 D、22

查看试题解析
8. 如图所示，在一幅矩形风景画的四周镶一条相同宽度的边框，制成一幅长为80cm，宽为50cm的挂图，设边框的宽为xcm，如果风景画的面积是2800cm² ，下列方程正确的是（）

A、（50+x）（80+x）＝2800 B、（50+2x）（80+2 x）＝2800 C、（50﹣x）（80﹣x）＝2800 D、（50﹣2x）（80﹣2x）＝2800

查看试题解析
9. 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，若旋转角为20°，则∠1为（）

A、110° B、120° C、150° D、160°

查看试题解析
10. 已知二次函数y＝（x﹣p）（x﹣q）+2，若m，n是关于x方程（x﹣p）（x﹣q）+2＝0的两个根，则实数m，n，p，q的大小关系可能是（）

A、m＜p＜q＜n B、m＜p＜n＜q C、p＜m＜n＜q D、p＜m＜q＜n

查看试题解析

二、填空题

11. 已知x＝1是方程x²﹣a＝0的根，则a＝．

查看试题解析
12. 从实数﹣1、﹣2、1中随机选取两个数，积为负数的概率是．

查看试题解析
13. 如图，△DEC与△ABC关于点C成中心对称，AB＝3，AC＝1，∠D＝90°，则AE的长是．

查看试题解析
14. 已知一个扇形的圆心角为100°，半径为4，则此扇形的弧长是．

查看试题解析
15. 如图，▱ABCD的对角线AC在y轴上，原点O为AC的中点，点D在第一象限内，AD∥x轴，当双曲线y＝ $\frac{4}{x}$ 经过点D时，则▱ABCD面积为．

查看试题解析
16. 如图，△ABO为等边三角形，OA＝4，动点C在以点O为圆心，OA为半径的⊙O上，点D为BC中点，连接AD，则线段AD长的最小值为．

查看试题解析

三、解答题

17. 解方程：

(1)、x²＝9；

(2)、x²+3x﹣5＝0．

查看试题解析
18. 已知关于x的一元二次方程x²+（2k+1）x+k²+k＝0．求证：无论k为何值，方程总有两个不相等的实数根．

查看试题解析

19. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共5只．某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：

摸球的次数n	100	150	200	500	800	1000
摸到白球的次数m	58	96	116	295	484	601
摸到白球的频率 $\frac{m}{n}$	0.58	0.64	0.58	0.59	0.605	0.601

(1)、请估计：当n很大时，摸到白球的频率将会接近（结果精确到0.1）；

(2)、试估算口袋中黑球有只，白球有只；

(3)、在（2）的结论下，请你用列表或树状图求出随机摸出两个球都是白球的概率．

查看试题解析

20. 如图，在边长为1的正方形网格中，△ABO的顶点均在格点上，点A，B的坐标分别是A（2，2），B（1，3），把△ABO绕点O逆时针旋转90°后得到△A₁B₁O．

(1)、画出△A₁B₁O，直接写出点A₁ ， B₁的坐标；

(2)、求在旋转过程中，△ABO所扫过的面积．

查看试题解析
21. 商场服装柜在销售中发现：某牌童装平均每天可售出20件，每件盈利40元．为了迎接“六一”儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存，经市场调查发现，如果每件童装每降价4元，那么平均每天就可多售出8件，

(1)、若商场要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少元？

(2)、若商场要想平均每天在销售这种童装上盈利最多，那么每件童装应降价多少元？

查看试题解析
22. 如图，在平面直角坐标系xOy中，点A在y轴上，∠OAB＝30°，B（2，0），OC⊥AB于点C，点C在反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象上．

(1)、求该反比例函数解析式；

(2)、若点D为反比例函数y＝ $\frac{k}{x}$ （k≠0）在第一象限的图象上一点，且∠DOC＝30°，求点D的坐标．

查看试题解析
23. 如图，AC，BD为四边形ABCD的对角线，∠ABC＝90°，∠ABD+∠ADB＝∠ACB，∠ADC＝∠BCD．

(1)、求证：AD⊥AC；

(2)、探求∠BAC与∠ACD之间的数量关系，并说明理由．

查看试题解析
24. 抛物线 $C_{1} ： y = - x^{2} + 2 m x - m^{2} + m + 3$ 的顶点为A，抛物线 $C_{2} ： y = - {(x + m + 4)}^{2} - m - 1$ 的顶点为B，其中m≠﹣2，抛物线 $C_{1}$ 与 $C_{2}$ 相交于点P．

(1)、当m＝﹣3时，在所给的平面直角坐标系中画出C₁ ， C₂的图象；

(2)、已知点C（﹣2，1），求证：点A，B，C三点共线；

(3)、设点P的纵坐标为q，求q的取值范围．

查看试题解析