福建省南安市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-24 类型:期末考试
一、单选题
-
1. 下列实数中,介于 与 之间的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 ; B、 ; C、 ; D、 .3. 为了让市民游客欢度“五一”,泉州市各地推出了许多文化旅游活动和景区优惠,旅游人气持续兴旺.从市文旅局获悉,“五一”假日全市累计接待国内外游客171.18万人次,171.18万这个数用科学记数法应表示为( )A、1.7118×10 B、0.17118×10 C、1.7118×10 D、171.18×104. 图①是由五个完全相同的小正方体组成的立体图形.将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
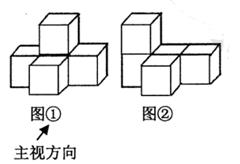 A、主视图 B、俯视图 C、左视图 D、主视图、俯视图和左视图都改变5. 不透明袋子中装有若干个红球和6个蓝球,这些球除了颜色外,没有其他差别,从袋子中随机摸出一个球,摸出蓝球的概率是0.6,则袋子中有红球( )A、4个 B、6个 C、8个 D、10个6. 如图,将直尺与含30°角的三角尺放在一起,若∠1=25°,则∠2的度数是( )
A、主视图 B、俯视图 C、左视图 D、主视图、俯视图和左视图都改变5. 不透明袋子中装有若干个红球和6个蓝球,这些球除了颜色外,没有其他差别,从袋子中随机摸出一个球,摸出蓝球的概率是0.6,则袋子中有红球( )A、4个 B、6个 C、8个 D、10个6. 如图,将直尺与含30°角的三角尺放在一起,若∠1=25°,则∠2的度数是( )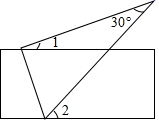 A、30° B、45° C、55° D、60°7. 如果一个正多边形的内角和等于720°,那么这个正多边形的每一个外角等于( )A、45° B、60° C、120° D、135°8. 如图,在平面直角坐标系中,菱形ABCD的边AB在x轴正半轴上,点A与原点重合,点D的坐标是 (3,4),反比例函数y= (k≠0)经过点C,则k的值为( )
A、30° B、45° C、55° D、60°7. 如果一个正多边形的内角和等于720°,那么这个正多边形的每一个外角等于( )A、45° B、60° C、120° D、135°8. 如图,在平面直角坐标系中,菱形ABCD的边AB在x轴正半轴上,点A与原点重合,点D的坐标是 (3,4),反比例函数y= (k≠0)经过点C,则k的值为( )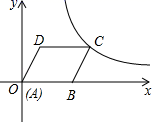 A、12 B、15 C、20 D、329. 完全相同的6个小矩形如图所示放置,形成了一个长、宽分别为n、m的大矩形,则图中阴影部分的周长是( )
A、12 B、15 C、20 D、329. 完全相同的6个小矩形如图所示放置,形成了一个长、宽分别为n、m的大矩形,则图中阴影部分的周长是( )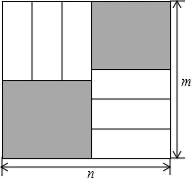 A、6(m﹣n) B、3(m+n) C、4n D、4m10. 如图,矩形ABCD中,E是AB的中点,将△BCE沿CE翻折,点B落在点F处,tan∠BCE= .设AB=x,△ABF的面积为y,则y与x的函数图象大致为
A、6(m﹣n) B、3(m+n) C、4n D、4m10. 如图,矩形ABCD中,E是AB的中点,将△BCE沿CE翻折,点B落在点F处,tan∠BCE= .设AB=x,△ABF的面积为y,则y与x的函数图象大致为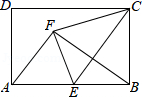 A、
A、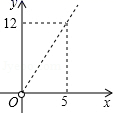 B、
B、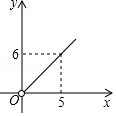 C、
C、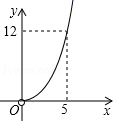 D、
D、
二、填空题
-
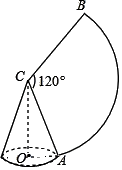
11. 计算:|﹣3|﹣sin30°= .12. 已知一组数据:12,10,8,15,6,8.则这组数据的中位数是 .13. 如图,圆锥侧面展开得到扇形,此扇形半径 CA=6,圆心角∠ACB=120°, 则此圆锥高 OC 的长度是 .
 14. 如图,量角器外沿上有A、B两点,它们的读数分别是75°、45°,则∠1的度数为.
14. 如图,量角器外沿上有A、B两点,它们的读数分别是75°、45°,则∠1的度数为.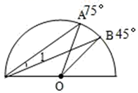 15. 等腰Rt△ABC中,斜边AB=12,则该三角形的重心与外心之间的距离是 .16. 动点A(m+2,3m+4)在直线l上,点B(b,0)在x轴上,如果以B为圆心,半径为1的圆与直线l有交点,则b的取值范围是 .
15. 等腰Rt△ABC中,斜边AB=12,则该三角形的重心与外心之间的距离是 .16. 动点A(m+2,3m+4)在直线l上,点B(b,0)在x轴上,如果以B为圆心,半径为1的圆与直线l有交点,则b的取值范围是 .三、解答题
-
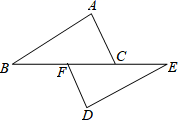
17. 解不等式组,并把解集在数轴上表示出来:18. 如图:△ABC与△DEF中,边BC,EF在同一条直线上,AB∥DE,AC∥DF,且BF=CE,求证:AC=DF.
 19. 先化简,再求值: ,其中x=1﹣ .20. 用列代数式或列方程(组)的方法,解决网络上流行的一个问题:法国新总统比法国第一夫人小24岁,美国新总统比美国第一夫人大24岁,法国新总统比美国新总统小32岁.求:美国第一夫人比法国第一夫人小多少岁?21. 在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
19. 先化简,再求值: ,其中x=1﹣ .20. 用列代数式或列方程(组)的方法,解决网络上流行的一个问题:法国新总统比法国第一夫人小24岁,美国新总统比美国第一夫人大24岁,法国新总统比美国新总统小32岁.求:美国第一夫人比法国第一夫人小多少岁?21. 在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:类别
家庭藏书m本
学生人数
A
0≤m≤25
20
B
26≤m≤50
a
C
51≤m≤75
50
D
m≥76
66
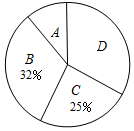
根据以上信息,解答下列问题:
(1)、该调查的样本容量为 , a=;(2)、随机抽取一位学生进行调查,刚好抽到A类学生的概率是;(3)、若该校有2000名学生,请估计全校学生中家庭藏书不少于76本的人数.22. 阅读下列材料,关于x的方程:x+ =c+ 的解是x1=c,x2= ;x﹣ =c﹣ 的解是x1=c,x2=﹣ ;x+ =c+ 的解是x1=c,x2= ;x+ =c+ 的解是x1=c,x2= ;……(1)、请观察上述方程与解的特征,比较关于x的方程x+ =c+ (a≠0)与它们的关系猜想它的解是什么,并利用“方程的解”的概念进行验证.(2)、可以直接利用(1)的结论,解关于x的方程:x+ =a+ .23. 如图,在Rt△ABC中,∠ACB=90°.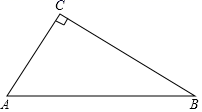 (1)、利用尺规作图,在BC边上求作一点P,使得点P到边AB的距离等于PC的长;(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)(2)、在(1)的条件下,以点P为圆心,PC长为半径的⊙P中,⊙P与边BC相交于点D,若AC=6,PC=3,求BD的长.24. 如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”,这条中线为“匀称中线”.
(1)、利用尺规作图,在BC边上求作一点P,使得点P到边AB的距离等于PC的长;(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)(2)、在(1)的条件下,以点P为圆心,PC长为半径的⊙P中,⊙P与边BC相交于点D,若AC=6,PC=3,求BD的长.24. 如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”,这条中线为“匀称中线”.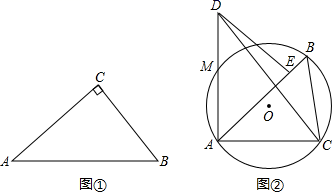 (1)、如图①,在Rt△ABC中,∠C=90°,AC>BC,若Rt△ABC是“匀称三角形”.
(1)、如图①,在Rt△ABC中,∠C=90°,AC>BC,若Rt△ABC是“匀称三角形”.①请判断“匀称中线”是哪条边上的中线,
②求BC:AC:AB的值.
(2)、如图②,△ABC是⊙O的内接三角形,AB>AC,∠BAC=45°,S△ABC=2 ,将△ABC绕点A逆时针旋转45°得到△ADE,点B的对应点为D,AD与⊙O交于点M,若△ACD是“匀称三角形”,求CD的长,并判断CM是否为△ACD的“匀称中线”.25. 已知:抛物线y=2ax2﹣ax﹣3(a+1)与x轴交于点AB(点A在点B的左侧).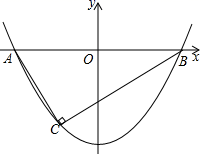 (1)、不论a取何值,抛物线总经过第三象限内的一个定点C,请直接写出点C的坐标;(2)、如图,当AC⊥BC时,求a的值和AB的长;(3)、在(2)的条件下,若点P为抛物线在第四象限内的一个动点,点P的横坐标为h,过点P作PH⊥x轴于点H,交BC于点D,作PE∥AC交BC于点E,设△ADE的面积为S,请求出S与h的函数关系式,并求出S取得最大值时点P的坐标.
(1)、不论a取何值,抛物线总经过第三象限内的一个定点C,请直接写出点C的坐标;(2)、如图,当AC⊥BC时,求a的值和AB的长;(3)、在(2)的条件下,若点P为抛物线在第四象限内的一个动点,点P的横坐标为h,过点P作PH⊥x轴于点H,交BC于点D,作PE∥AC交BC于点E,设△ADE的面积为S,请求出S与h的函数关系式,并求出S取得最大值时点P的坐标.