山西省朔州市右玉县二中2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期:2020-11-24 类型:月考试卷
一、单选题
-
1. 下列长度的三根小木棒能构成三角形的是( )A、2cm,3cm,5cm B、7cm,4cm,2cm C、3cm,4cm,8cm D、3cm,3cm,4cm2. 下列各组图形中,AD是 的高的图形是( )A、
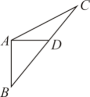
B、
B、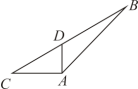
C、
C、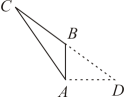
D、
D、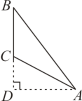
3. 下列说法:
3. 下列说法:①全等三角形的形状相同、大小相等
②全等三角形的对应边相等、对应角相等
③面积相等的两个三角形全等
④全等三角形的周长相等
其中正确的说法为( )
A、①②③④ B、①②③ C、②③④ D、①②④4. 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,若∠BFC=116°,则∠A=( )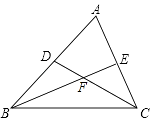 A、51° B、52° C、53° D、58°5. 如图,△ABC中,∠C=80°,若沿图中虚线截去∠C,则∠1+∠2=( )
A、51° B、52° C、53° D、58°5. 如图,△ABC中,∠C=80°,若沿图中虚线截去∠C,则∠1+∠2=( ) A、360° B、260° C、180° D、140°6. 设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是( )A、
A、360° B、260° C、180° D、140°6. 设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是( )A、 B、
B、 C、
C、 D、
D、 7. 已知三角形的三边长分别为4,a , 8,那么下列在数轴上表示该三角形的第三边a的取值范围正确的是( )A、
7. 已知三角形的三边长分别为4,a , 8,那么下列在数轴上表示该三角形的第三边a的取值范围正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图所示,下列结论不能确定的是( )
8. 如图所示,下列结论不能确定的是( )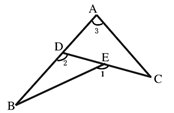 A、∠1>∠2 B、∠2 >∠C C、∠3>∠B D、∠1>∠39. 在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
A、∠1>∠2 B、∠2 >∠C C、∠3>∠B D、∠1>∠39. 在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )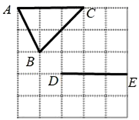 A、2个 B、4个 C、6个 D、8个10. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
A、2个 B、4个 C、6个 D、8个10. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )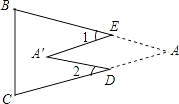 A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)
A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)二、填空题
-
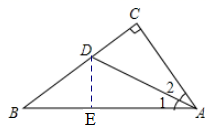
11. 要想使一个六边形活动支架ABCDEF稳固且不变形,至少需要增加根木条才能固定.12. 已知一个等腰三角形的两条边长分别是2cm和7cm,则此三角形的周长为cm.13. 在 中,如果 ,根据三角形按角进行分类,这个三角形是三角形. 度.14. 如图, , ,若 , ,则D到AB的距离为。
 15. 如图, ,若要使 ,应添加的关于边的条件是 , 应添加的关于角的条件是 . (只需填写一个正确条件)
15. 如图, ,若要使 ,应添加的关于边的条件是 , 应添加的关于角的条件是 . (只需填写一个正确条件)
三、解答题
-
16. 如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
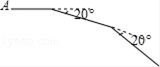 (1)、小明一共走了多少米?(2)、这个多边形的内角和是多少度?17. 如图,△ABC中,AB=AC,且AC上的中线BD把这个三角形的周长分成了12cm和6cm的两部分,求这个三角形的腰长和底边的长.
(1)、小明一共走了多少米?(2)、这个多边形的内角和是多少度?17. 如图,△ABC中,AB=AC,且AC上的中线BD把这个三角形的周长分成了12cm和6cm的两部分,求这个三角形的腰长和底边的长. 18. 如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
18. 如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线. (1)、∠1与∠2有什么关系,为什么?(2)、BE与DF有什么关系?请说明理由.19. 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB.
(1)、∠1与∠2有什么关系,为什么?(2)、BE与DF有什么关系?请说明理由.19. 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB. 20. 如图,AB=AE,∠B=∠AED,∠1=∠2.求证:△ABC≌△AED.
20. 如图,AB=AE,∠B=∠AED,∠1=∠2.求证:△ABC≌△AED.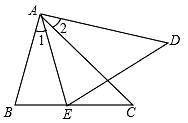 21. 如图,已知点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AC∥DF。
21. 如图,已知点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AC∥DF。 22. 如图,△ABC中,点E , F分别在边CB及其延长线上,且CE=BF , DF∥AC , 且DF=AC , 连接DE , 求证:∠A=∠D .
22. 如图,△ABC中,点E , F分别在边CB及其延长线上,且CE=BF , DF∥AC , 且DF=AC , 连接DE , 求证:∠A=∠D . 23. 如图,按下列要求作图:作出△ABC的角平分线CD;(不写作法,保留作图痕迹)
23. 如图,按下列要求作图:作出△ABC的角平分线CD;(不写作法,保留作图痕迹)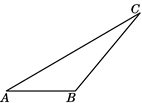 24. 如图,A , B两建筑物位于河的两岸,要测它们之间的距离,可以从B点出发在河岸上画一条射线BF , 在BF上截取BC=CD , 过D作DE∥AB , 使E , C , A在同一直线上,则DE的长就是A , B之间的距离,请你说明道理.
24. 如图,A , B两建筑物位于河的两岸,要测它们之间的距离,可以从B点出发在河岸上画一条射线BF , 在BF上截取BC=CD , 过D作DE∥AB , 使E , C , A在同一直线上,则DE的长就是A , B之间的距离,请你说明道理. 25. 阅读下列材料,并完成相应的任务.
25. 阅读下列材料,并完成相应的任务.基本性质:三角形中线等分三角形的面积.
如图, 是 的边 上的中线,

则
理由:过点A作 于点H
∵ 是 的边 上的中线.
∴ 又∵ ,
∴
∴三角形中线等分三角形的面积.
任务:
(1)、如图,延长 的边 到点D,使 ,连接 ,则 和 的数量关系为. (2)、如图,点D是 的边 上任意一点,点 分别是线段 , 的中点,且 的面积为 ,请同学们借助上述结论求 的面积.
(2)、如图,点D是 的边 上任意一点,点 分别是线段 , 的中点,且 的面积为 ,请同学们借助上述结论求 的面积. 26. 如图,在△ABC中,AB=AC , DE是过点A的直线,BD⊥DE于点D , CE⊥DE于点E .
26. 如图,在△ABC中,AB=AC , DE是过点A的直线,BD⊥DE于点D , CE⊥DE于点E . (1)、若B、C在DE的同侧(如图所示),且AD=CE . 求证:AB⊥AC;(2)、若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
(1)、若B、C在DE的同侧(如图所示),且AD=CE . 求证:AB⊥AC;(2)、若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.